As shown in (Fig. 3.90), two large parallel vertical conducting plates separated by distance D are charge so that their potential are +V0 and −V0. A small conducting ball of mass m and radius r (whereR<<d) is hung midway between the plates. The thread of length L supporting the ball is a conducting wire connected to ground, so the potential of the ball is fixed at V=0. The ball hangs straight down in stable equilibrium when V0 is sufficiently small. Show that the equilibrium of the ball is unstable if V0 exceeds the critical value [ked2mg/(4RL)]1/2.

The plates create uniform electric field to the right in the picture, with magnitude [V0−(−V0)]/d=2V0/d. Assume the ball swings a small distance x to the right. It moves to a place where the voltage created by the plates is lower by
−Ex=−2V0dx
Its ground connection maintains it at V=0 by allowing charge q to flow from ground onto the ball, where −2V0xd+keqR=0
q=2V0xRked
Then the ball feels electric force
F=qE=4V20xRked2 to the right.
for equilibrium, this must be balanced by the horizontal component of string tension according to Tcosθ=mg
Tsinθ=4V20xRked2tanθ=4V20xRked2mg=xL for small x
Then V0=(ked2mg4RL)1/2
If V0 is less than this value, the only equilibrium position of the ball is hanging straight down. If V0 exceeds this value, the ball will saving over to one plate or the other.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
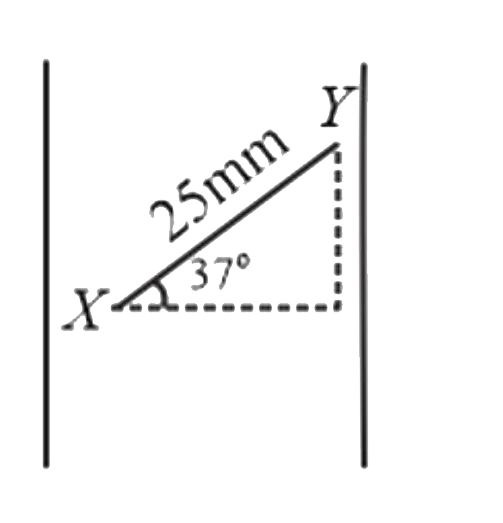
Two large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
View SolutionFour conducting plates of equal area A are separated by distance d and are arranged as shown.The equivalent capacitance between A and B is
_PHY_E05_294_Q01.png)
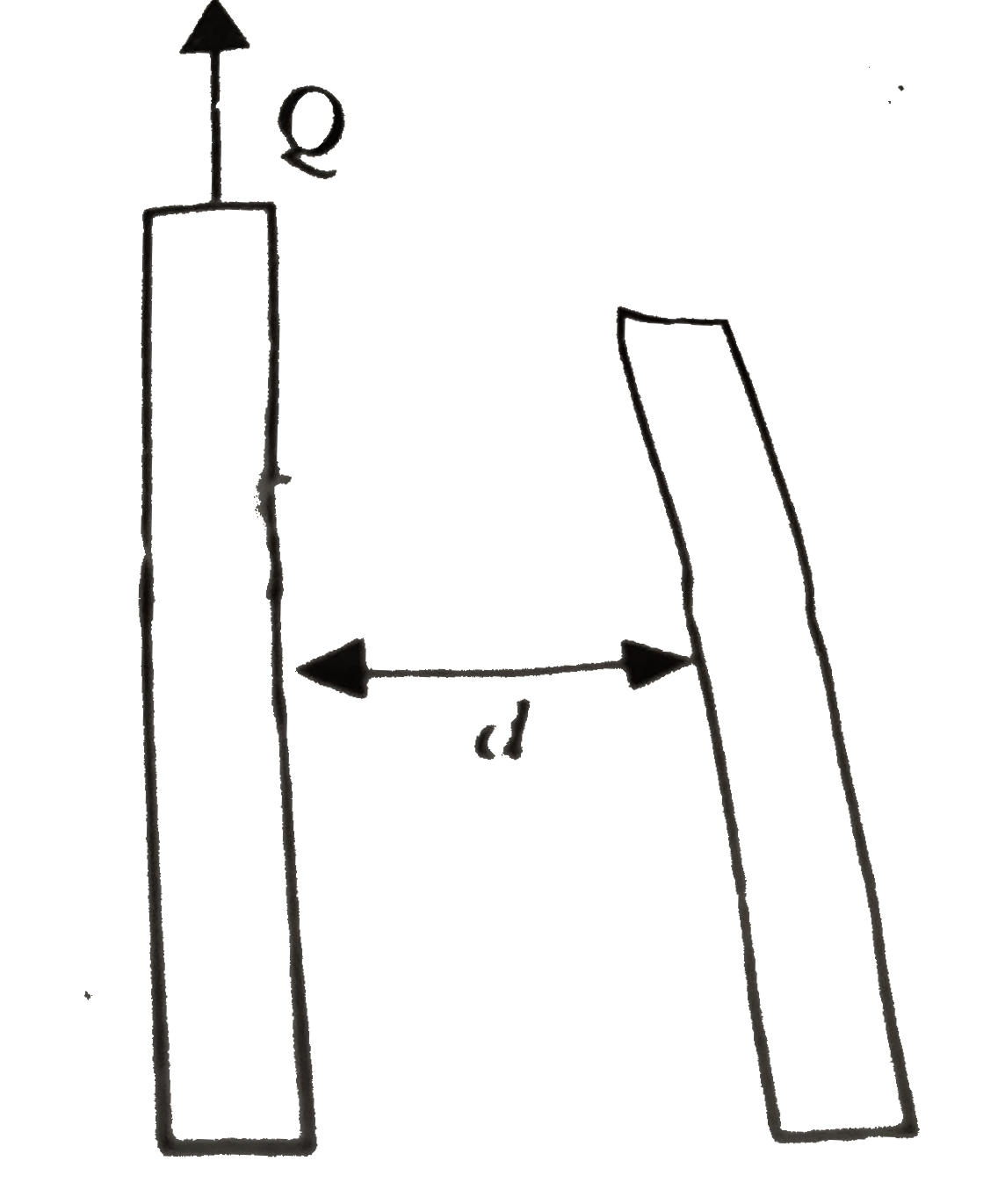
View SolutionTwo parallel conducting plates, each of area A, are separated by a distance d. Now, the left plate is given a positive charge Q. A positive charge q of mass m is released from a point near the left plate. Find the time taken by the charge to reach the right plate.
View SolutionFour parallel large plates separated by equal distance d are arranged as shown in. The area of the plates is S Find the potential differnce between plats BandC if plate B is given a charge Q.
 .
.
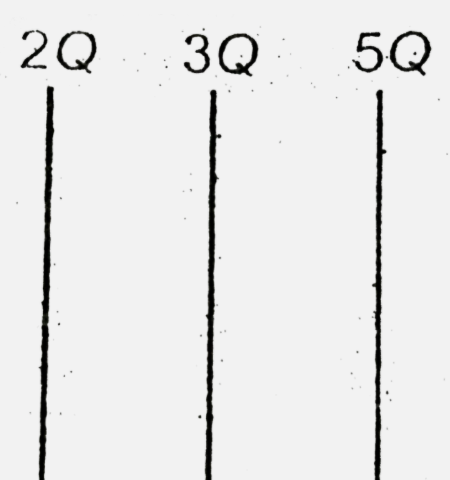
View SolutionThree charged conducting plates are separated by small distances as shown in figure. The charges on the plates are shown. Find the ratio of charge on right surface and left surface of the middle plate.
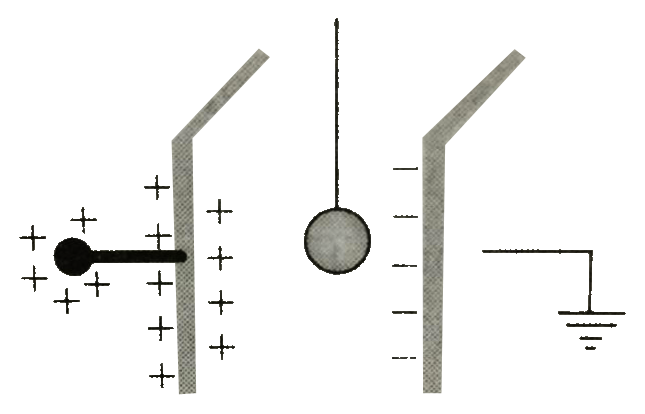
View SolutionA table tennis ball covered with a conducting paint is suspended by a silk thread so that it hangs between tow metal plates. One plate is earthed, when the other plate is connected to a high voltage generator, what will happen to the ball.
View SolutionFive conducting parallel plates having area A and separation between them d, are placed as shown in the fig. Plate number 2 and 4 are connected with a conducting wire and between point A and B a cell of emf. .ε. is connected . The change flows through the cell is
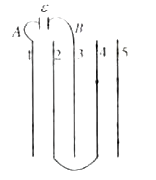
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final electric potential of sphere of radius 3R will be :
View SolutionA parallel plate capacitor of plate area A and plates separation distance d is charged by applying a potential V0 between the plates. The dielectric constant of the medium between the plates is K. What is the uniform electric field E between the plates of the capacitor ?
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
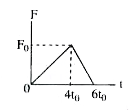
Average force exerted by the bat on the ball is
View Solution