A point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.
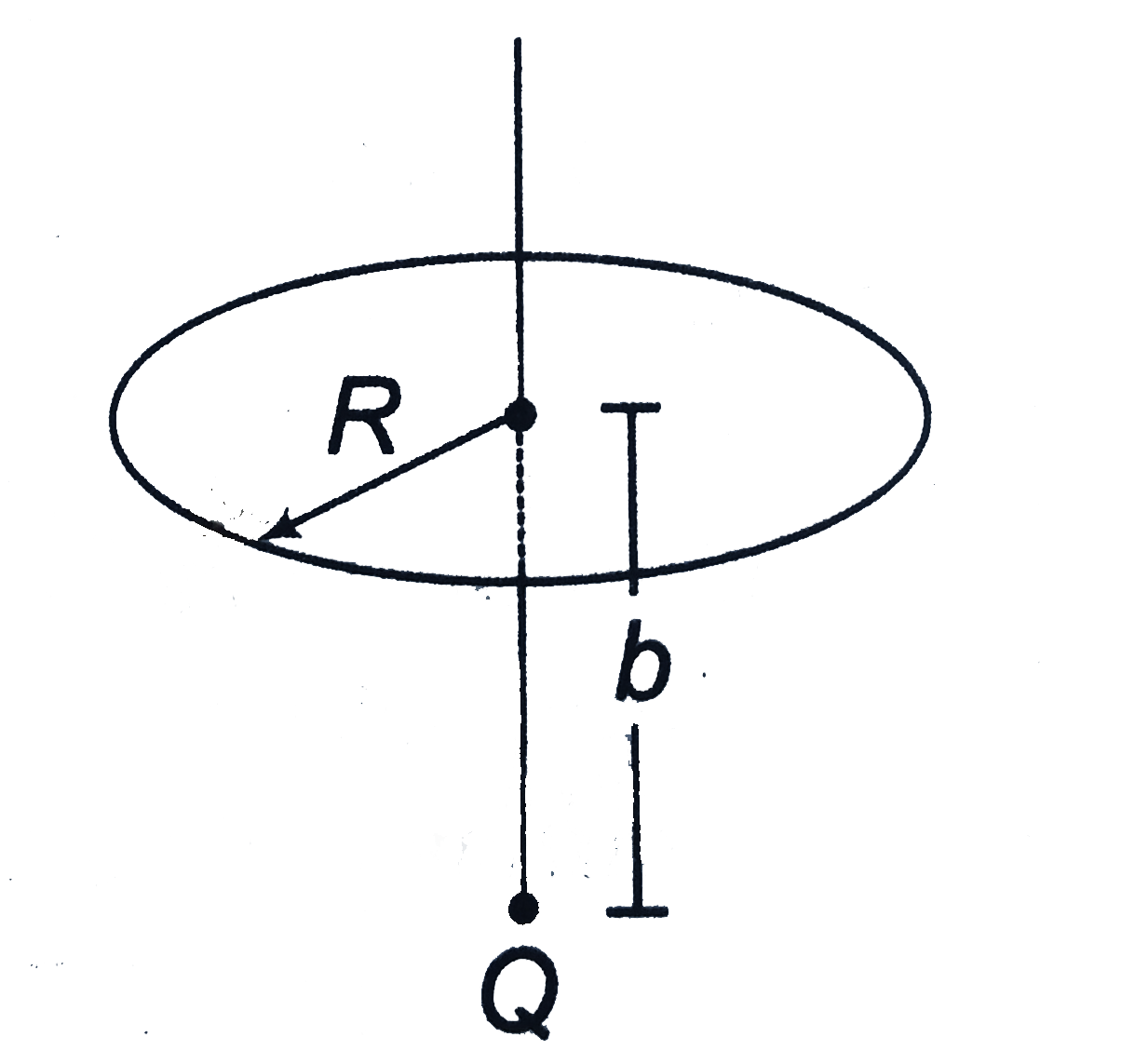
The correct Answer is:√3b
Solid angle subtended by disk at Q is
Ω=2π(1−cosα)
=2π[1−b√b2+R2]
Flux through disk is (QΩ)/(ε04π)
It is given to be Q/4ε0.
So, Q4ε0=QΩε04π
Solve to get R =√3b.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct40videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.214videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disk. If one - fourth of the electric flux from the charge passes through the disk, then R=√kb. Find k.
 View Solution
View SolutionA positive point charge Q is placed (on the axis of disc) at a distance of 4 R . Above the centre of a disc of radius R as shown in situation I. the magnitude of electric flux through the disc is (ϕ). Now a hemis pherical shell of radius R is placed over the disc. such that it forms a closed surface as shown in situation II. The flux through the curved suface in situation II taking direction of area vector along outward normal as positive is
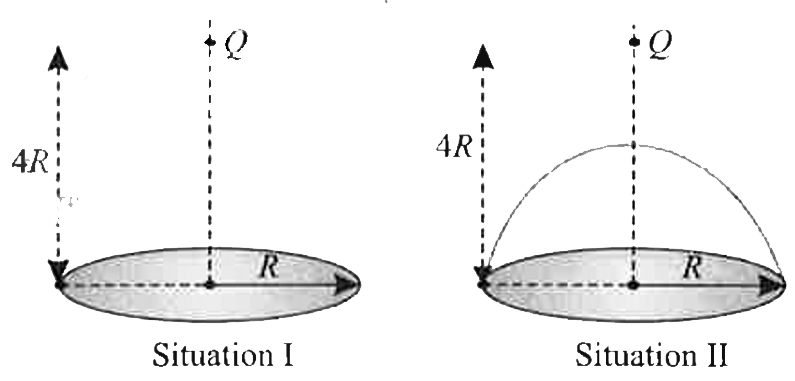 View Solution
View SolutionA point charge q is placed at a point on the axis of a non-conducting circular plate of radius r at a distance R(>>r) from its center. The electric flux associated with the plate is
View SolutionA point charge placed on the axis of a uniformly charged disc experiences a force f due to the disc. If the charge density on the disc σ is, the electric flux through the disc, due to the point charge will be
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
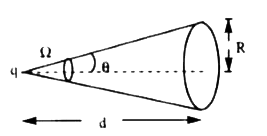 View Solution
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 View Solution
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
View Solution
