Find the electric flux crossing the wire frame ABCD of length l, width b, and center at a distance OP = d from an infinite line of charge with linear charge density λ. Consider that the plane of the frame is perpendicular to the line OP

The correct Answer is:λlπε0tan−1(b2d)
The flux passing through the strip of area dA is
dϕ=EdAcosθ
=λ2πε0√d2+x2(ldx)d√d2+x2
=λdl2πε0dxd2+x2
∴Φ=∫dϕ=λdl2πε0∫b/2−b/2dxd2+x2
=λdl2πε01d[tan−1xd]b/2−b/2
=λl2πε0×2tan−1(b2d)
=λlπε0tan−1(b2d)
 , (##BMS_V03_C02_E01_039_S02.png) .
.
Alternative method
The number of lines passing through a surface is proportional to the
flux passing through the surface. The number of lines passing through
the plane surface ABCD is equal to the number of lines passing
through the curved surface. The amount of flux passing through the
plane surface is equal to the line flux passing through the curved
surface.
From figure , tan(θ2)=(b2d)orθ=2tan−1(b2d)
2π angle corresponds to flux λl/ε0.
Hence, θ angle corresponds to the flux, i.e.,
ϕ=θ2π(λlε0)=λlπε0tan−1(b2d)
 .
.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct
40 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.2
14 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
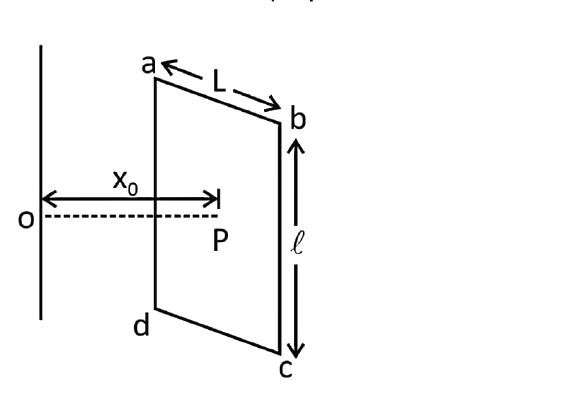
Find the electric flux (in S.I. unit) through the rectangular plate abcd of length l=2m width L and whose centre is at a distance OP=x0=L2 from an infinite line of charge with linear charge density λ=136π×10−9Cm−1. Consider that the plate of the frame is perpendicular to line OP.
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
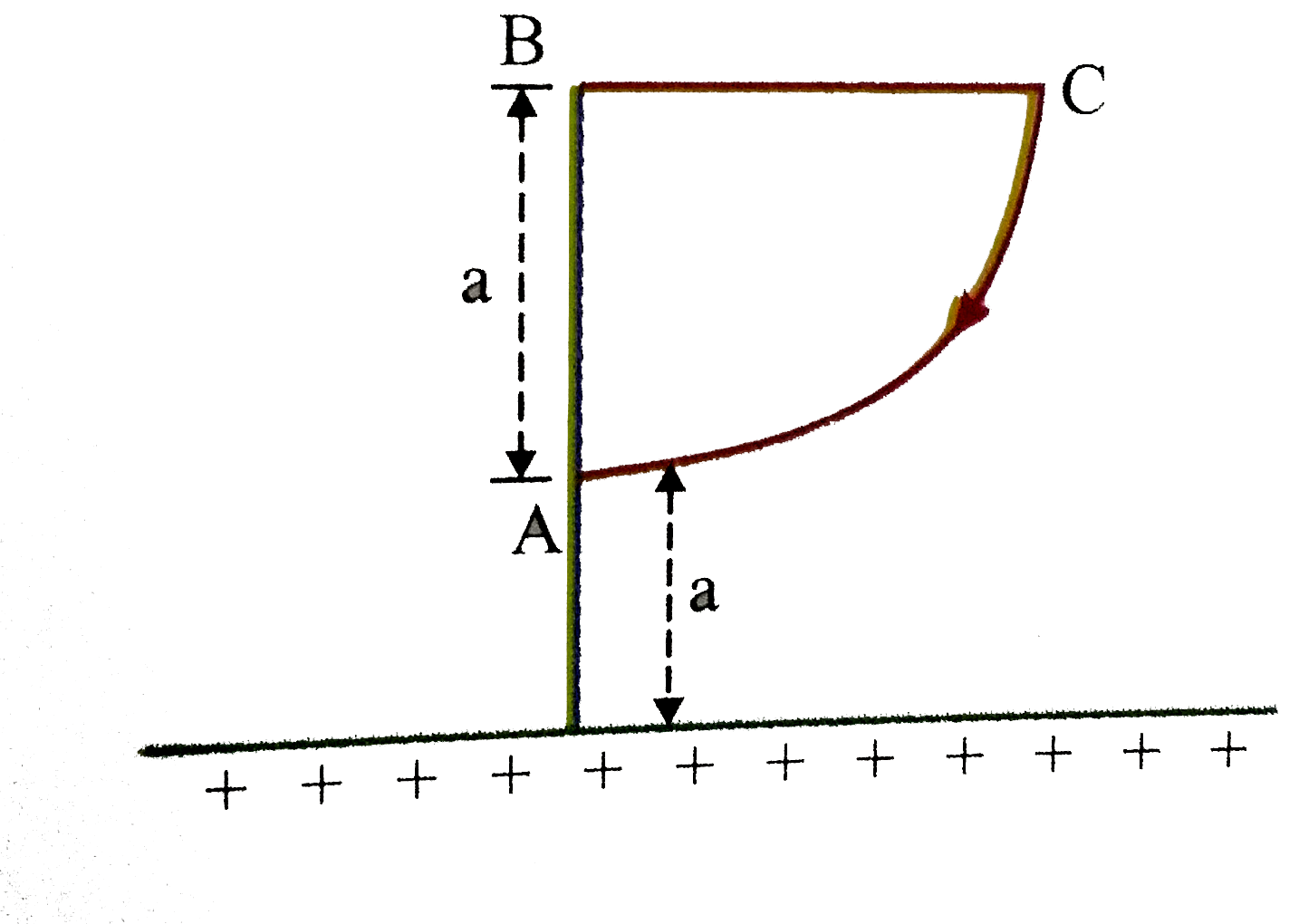
View SolutionFor an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.

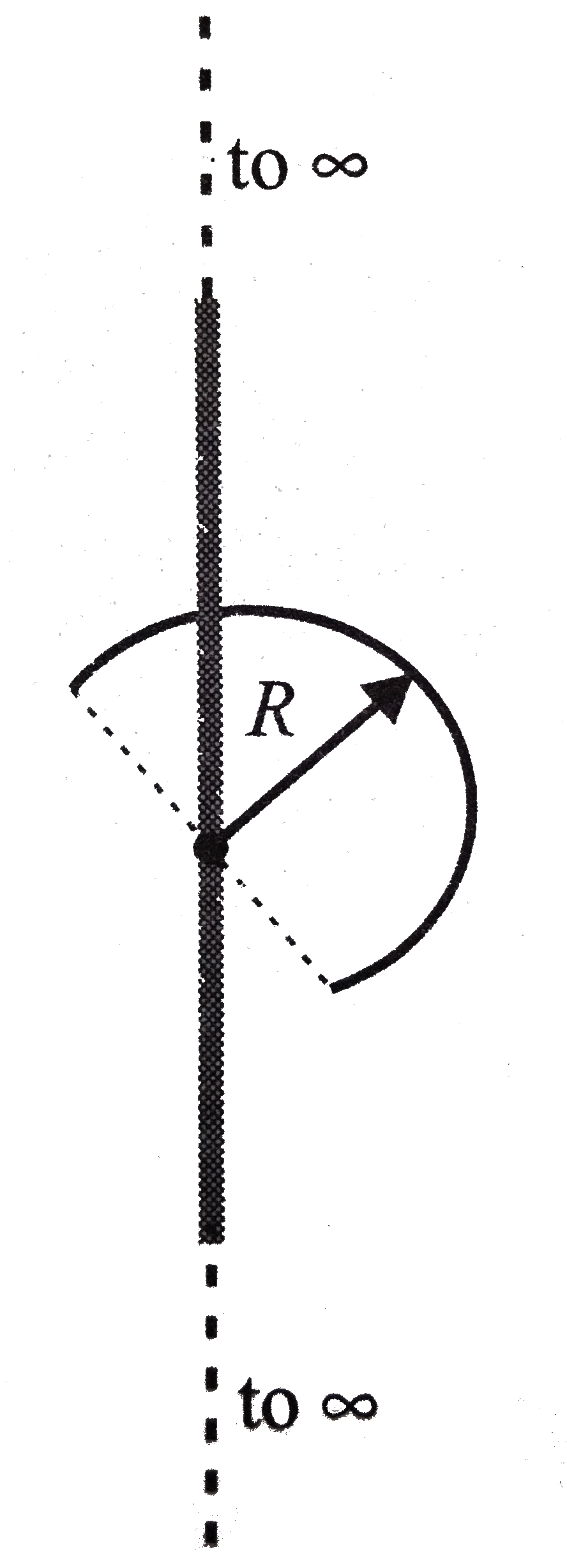
View SolutionFind the force experienced by a semicircular rod having a charge q as shown in fig. Radius of the wire is R, and the line of charge with linear charge density λ passes through its center and is perpendicular to the plane of wire.
View SolutionIntensity of electric field at a perpendicular distance of 0.5 m from an infinitely long line charge having linear charge density (λ) is 3.6×103Vm−1 . Find the value of λ
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png)
View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View Solution
