There is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a distance L/4 from one of its ends.
What is the time period of the SHM as mentioned in the above question, if an electric field E is applied along horizontal?

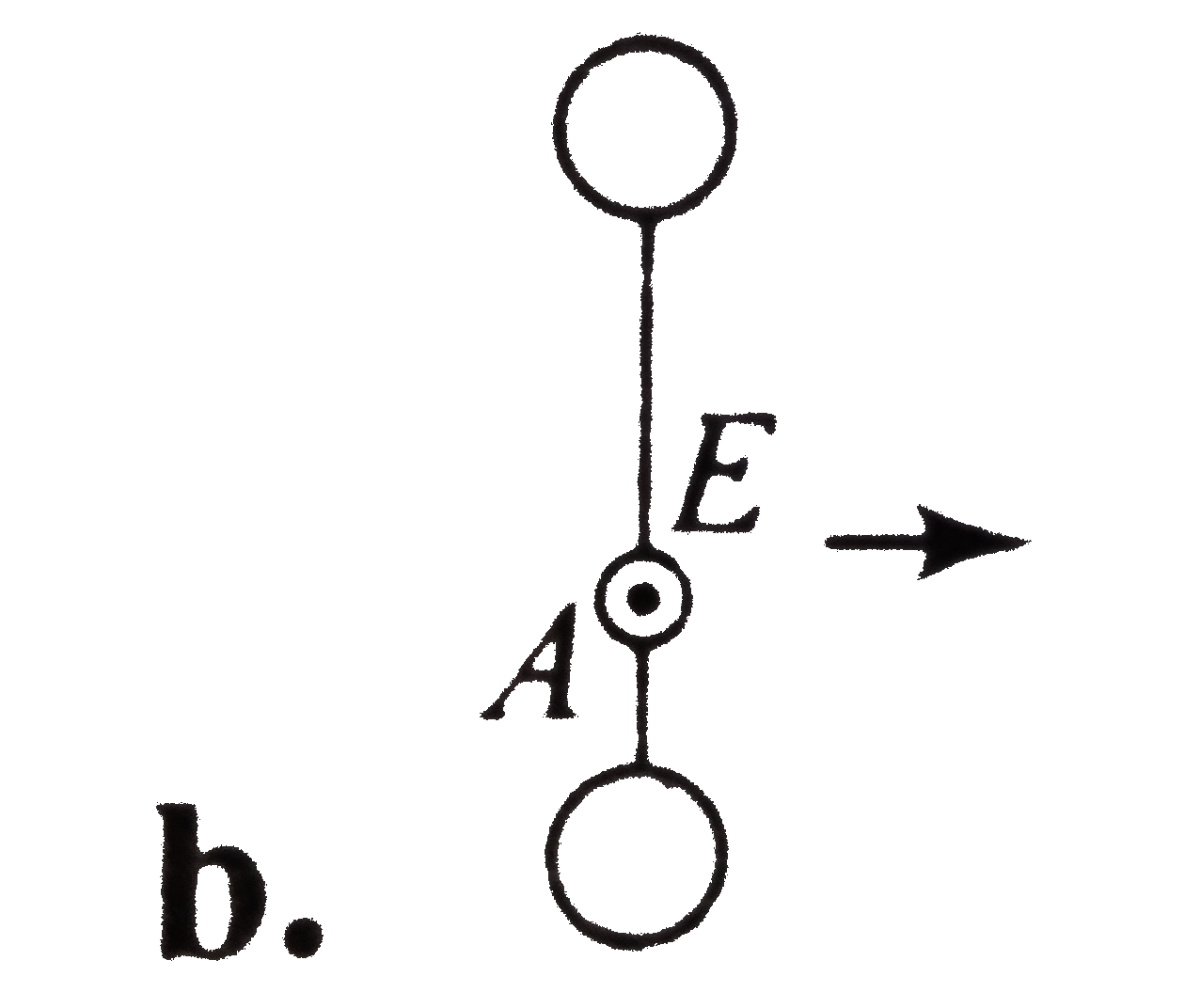
The correct Answer is:A
To solve the problem, we need to determine the time period of the simple harmonic motion (SHM) of the system described. Here’s a step-by-step solution:
Step 1: Understand the System
We have an insulating rod of length L with two small balls of mass m and charge Q attached to its ends. The rod can rotate about a vertical axis at a distance L4 from one end. An electric field E is applied horizontally.
Step 2: Identify the Forces Acting on the System
When the rod is displaced from its equilibrium position, the electric force acting on each ball due to the electric field is given by:
F=QE
This force will cause a torque about the pivot point.
Step 3: Calculate the Torque
The torque τ due to the electric force on each ball can be calculated. For the ball at a distance 3L4 from the pivot, the torque is:
τ1=(3L4)⋅QE⋅sin(θ)
For the ball at a distance L4 from the pivot, the torque is:
τ2=(L4)⋅QE⋅sin(θ)
The net torque τ acting on the system is:
τ=τ1−τ2=(3L4QE−L4QE)sin(θ)=(2L4QE)sin(θ)=LQE2sin(θ)
Step 4: Relate Torque to Angular Acceleration
According to Newton's second law for rotation, the torque is also related to the moment of inertia I and angular acceleration α:
τ=Iα
For the system, the moment of inertia I can be calculated as:
I=m(L4)2+m(3L4)2=m(L216+9L216)=m(10L216)=5mL28
Step 5: Set Up the Equation for SHM
Substituting the expression for torque into the equation for angular acceleration gives:
LQE2sin(θ)=5mL28α
Since for small angles sin(θ)≈θ and α=d2θdt2, we can write:
LQE2θ=5mL28d2θdt2
Step 6: Rearranging to Find the Angular Frequency
Rearranging gives:
d2θdt2+4QE5mLθ=0
This is the standard form of SHM, where the angular frequency ω2 is:
ω2=4QE5mL
Step 7: Calculate the Time Period
The time period T of SHM is given by:
T=2πω=2π√5mL4QE
Final Answer
Thus, the time period of the SHM is:
T=2π√5mL4QE
We have an insulating rod of length L with two small balls of mass m and charge Q attached to its ends. The rod can rotate about a vertical axis at a distance L4 from one end. An electric field E is applied horizontally.
When the rod is displaced from its equilibrium position, the electric force acting on each ball due to the electric field is given by:
F=QE
This force will cause a torque about the pivot point.
The torque τ due to the electric force on each ball can be calculated. For the ball at a distance 3L4 from the pivot, the torque is:
τ1=(3L4)⋅QE⋅sin(θ)
For the ball at a distance L4 from the pivot, the torque is:
τ2=(L4)⋅QE⋅sin(θ)
The net torque τ acting on the system is:
τ=τ1−τ2=(3L4QE−L4QE)sin(θ)=(2L4QE)sin(θ)=LQE2sin(θ)
According to Newton's second law for rotation, the torque is also related to the moment of inertia I and angular acceleration α:
τ=Iα
For the system, the moment of inertia I can be calculated as:
I=m(L4)2+m(3L4)2=m(L216+9L216)=m(10L216)=5mL28
Substituting the expression for torque into the equation for angular acceleration gives:
LQE2sin(θ)=5mL28α
Since for small angles sin(θ)≈θ and α=d2θdt2, we can write:
LQE2θ=5mL28d2θdt2
Rearranging gives:
d2θdt2+4QE5mLθ=0
This is the standard form of SHM, where the angular frequency ω2 is:
ω2=4QE5mL
The time period T of SHM is given by:
T=2πω=2π√5mL4QE
Thus, the time period of the SHM is:
T=2π√5mL4QE
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
There is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it ata distance L/4 from one of its ends.
At first the rod is in unstabele equillbrium in a Horizontal uniform electric field of field strenght E. Then we gently displace it from this position. Determine the maximim velocity attained by the ball taht is closer to the axis in the subsequent motion
View SolutionWhat will be the magnitude and polarity of induced emf across the rod, if it is rotating about an axis at a distance L4 from one of its ends.

View SolutionA light rigid rod of mass M, and length L is pivoted at one of its end. The rod can swing freely in the vertical plane through a horizontal axis passing through the pivot. Show that the time period of the rod about the pivot is T=π√2L3g
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
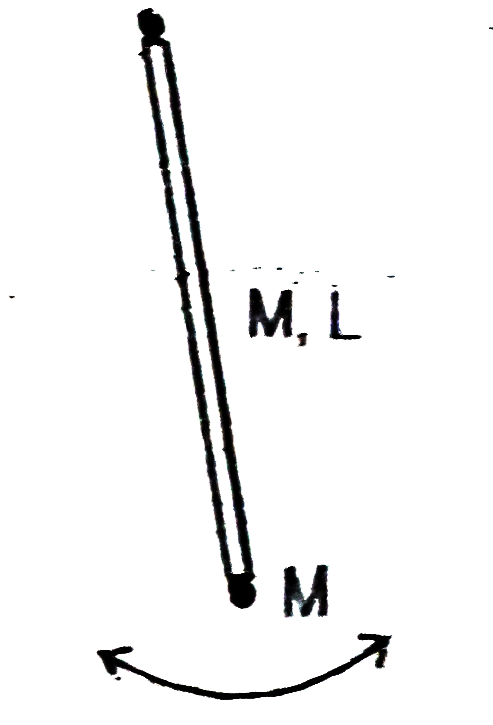
View Solution
