Two point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
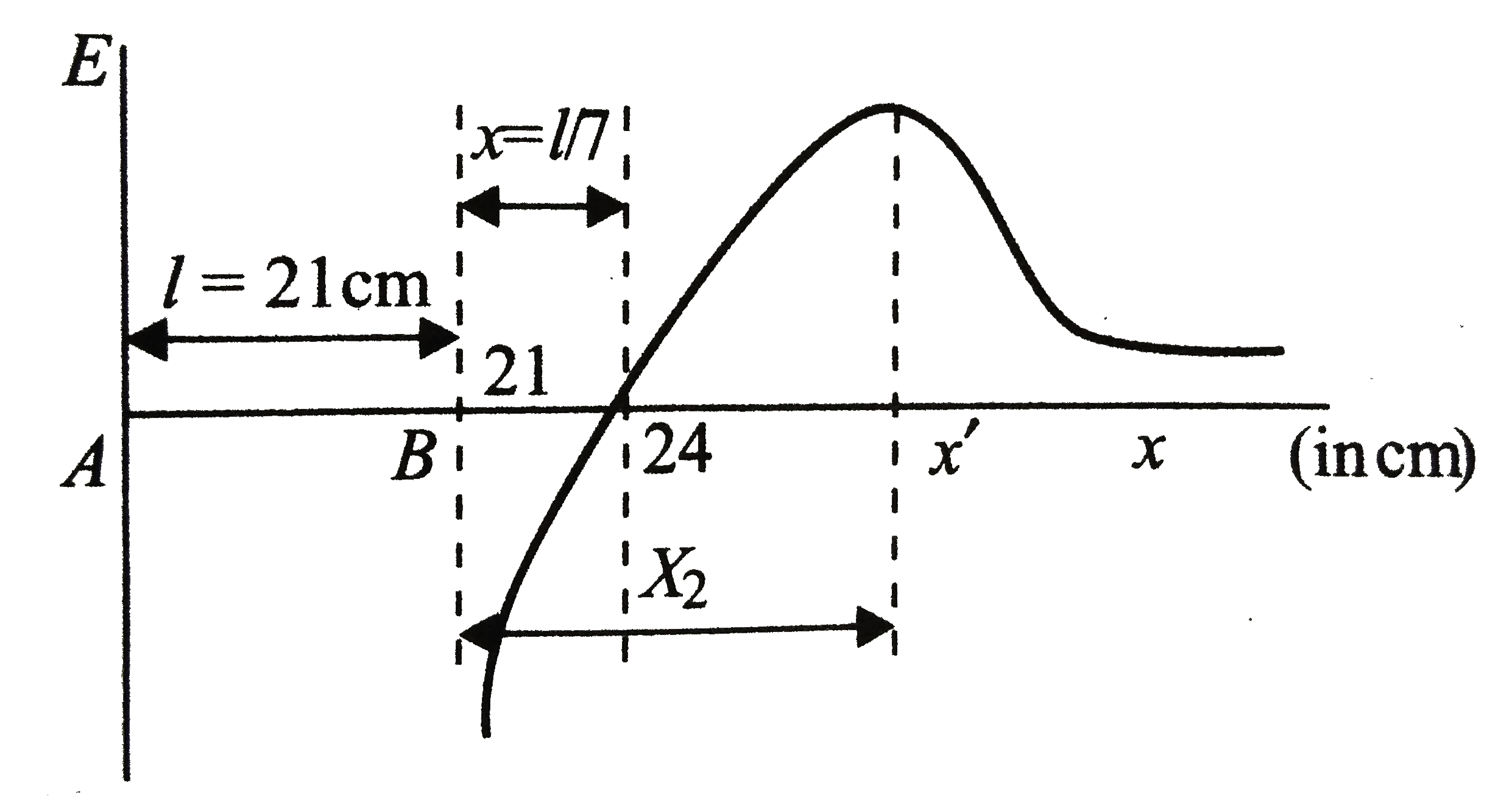
(a) Find the sign of the charges.
(b) Find the ratio between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
+,−
−,+
+,+
−,−
The correct Answer is:A
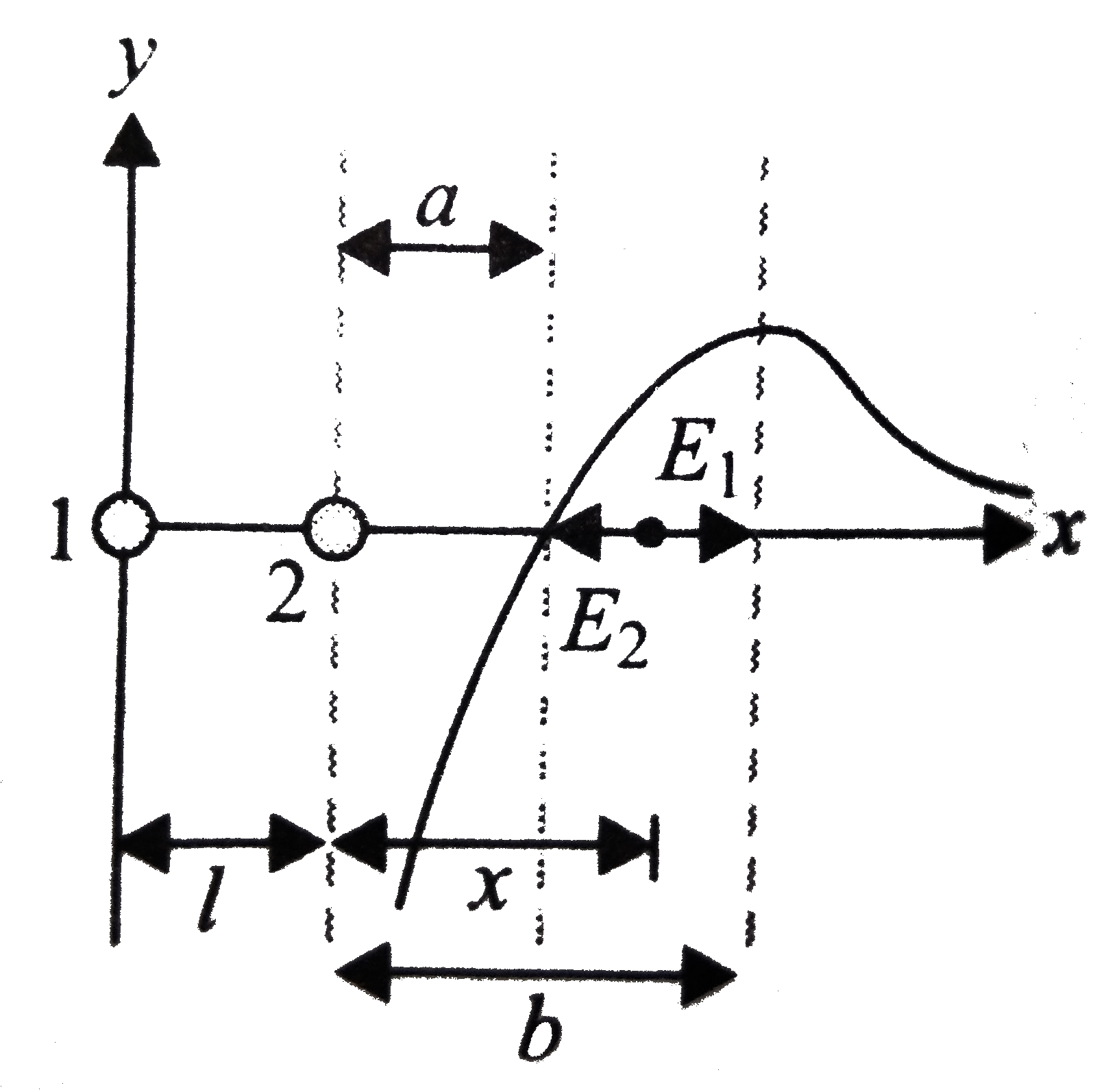
Electric field at (2) tends to −∞, hence the charge at (2) should be negative. There is a neutral point to the right of charges. This is possible onlu when the charge at (1) should be positive. Hence Q1 is positive and Q2 is negative. At netural point, →E1=→E2.
14πε0Q1(a+l)2=14πε0Q2a2 or Q1Q2=(a+la)2
Electric field at any position to the right of charges is
E=E1−E2=14πε0Q1(l+x)2−14πε0Q2x2
For the maximum value of E,
dEdx=0orddx[14πε0Q(l+x)2−14πε0Q2x2]=0
Q1−2(l+x)3−Q2−2x3=0
or Q1(l+x)3=Q2x3 or (l+xx)3=Q1Q2
or, l+xx=(Q1Q2)1/3 or lx=(Q1Q2)1/3−1
or x=l(Q1Q2)1/3−1.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.

View SolutionThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
View SolutionTwo fixed charges 4Q (positive) and Q (negative) are located at A and B. the distance AB being 3 m.
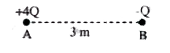
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.

View SolutionTwo charge +aq and -q are kept apart. Then , at any point on the right bisector of line joining the two charge
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionTwo point charges Q and -3Q are placed at some distance apart. If the electric field at the location of Q is →E, the field at the location of - 3Q is
View SolutionTwo point charges q and −q are separated by a distance 2l. Find the flux strength vector across the circle of radius R placed with its centre coinciding with the of line joining the two charges in the perpendicular plane.
View SolutionA positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View Solution
