Maximum excess pressure inside a thin-walled steel tube of radius r and thickness △r(<<r), so that the tube would not rupture would be (breaking stress of steel is σmax
σmax×r△r
σmax×△rr
σmax
σmax×△2rr
The correct Answer is:B
To solve the problem of finding the maximum excess pressure inside a thin-walled steel tube, we can follow these steps:
Step 1: Understand the Geometry and Forces
We have a thin-walled steel tube with radius r and thickness δr (where δr≪r). The tube experiences internal pressure, leading to tension in the walls of the tube.
Step 2: Draw a Free Body Diagram
Draw a cross-section of the tube and identify the forces acting on it. The tension T in the tube walls acts tangentially. The angle subtended at the center by the tension is 2θ.
Step 3: Apply Force Equilibrium
Using the equilibrium of forces, we can express the relationship between the tension and the pressure difference. The vertical components of the tension must balance the pressure acting on the area of the tube.
The force due to the internal pressure ΔP acting on the area of the tube can be expressed as:
Force due to pressure=ΔP×(2r⋅l)
where l is the length of the tube.
Step 4: Relate Tension and Pressure
From the geometry, the vertical component of the tension can be expressed as:
2Tsin(θ)≈2Tθ(for small θ)
Setting the two forces equal gives:
2Tθ=ΔP×(2r⋅l)
Cancelling the common factors (2 and θ):
T=ΔP⋅r⋅l
Step 5: Relate Tension to Stress
The breaking stress σmax of the material is defined as:
σmax=Tδr⋅l
Substituting for T from the previous step:
σmax=ΔP⋅r⋅lδr⋅l
Cancelling l from both sides:
σmax=ΔP⋅rδr
Step 6: Solve for Maximum Excess Pressure
Rearranging the equation to solve for ΔP:
ΔP=σmax⋅δrr
Final Result
Thus, the maximum excess pressure inside the thin-walled steel tube is given by:
ΔP=σmax⋅δrr
---
We have a thin-walled steel tube with radius r and thickness δr (where δr≪r). The tube experiences internal pressure, leading to tension in the walls of the tube.
Draw a cross-section of the tube and identify the forces acting on it. The tension T in the tube walls acts tangentially. The angle subtended at the center by the tension is 2θ.
Using the equilibrium of forces, we can express the relationship between the tension and the pressure difference. The vertical components of the tension must balance the pressure acting on the area of the tube.
Force due to pressure=ΔP×(2r⋅l)
where l is the length of the tube.
From the geometry, the vertical component of the tension can be expressed as:
2Tsin(θ)≈2Tθ(for small θ)
Setting the two forces equal gives:
2Tθ=ΔP×(2r⋅l)
Cancelling the common factors (2 and θ):
T=ΔP⋅r⋅l
The breaking stress σmax of the material is defined as:
σmax=Tδr⋅l
Substituting for T from the previous step:
σmax=ΔP⋅r⋅lδr⋅l
Cancelling l from both sides:
σmax=ΔP⋅rδr
Rearranging the equation to solve for ΔP:
ΔP=σmax⋅δrr
Thus, the maximum excess pressure inside the thin-walled steel tube is given by:
ΔP=σmax⋅δrr
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Subjective
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
Maximum pressure difference between inner and outer surface of a thin walled circular tube of radius r and thickness Δr(Δr<<r) so that tube won't break is (Breaking stress of the material is σ0)
View SolutionThe excess pressure inside a soap bubble of radius R is (S is the surface tension)
View SolutionThe maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
View SolutionCurrent flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
View SolutionThe excess pressure inside an air bubble of radius r just below the surface of water is P1. The excess pressure inside a drop of the same radius just outside the surface is P2. If T is surface tension then
View SolutionA stream of a liquid of density p flowin horizontally with speed v rushes out of a tube of radius r and hits a verticla wall nearly normally. Assumi g that the liquid does not rebound from the wall, the force exerted o the wall by the impact of the liquid is given by
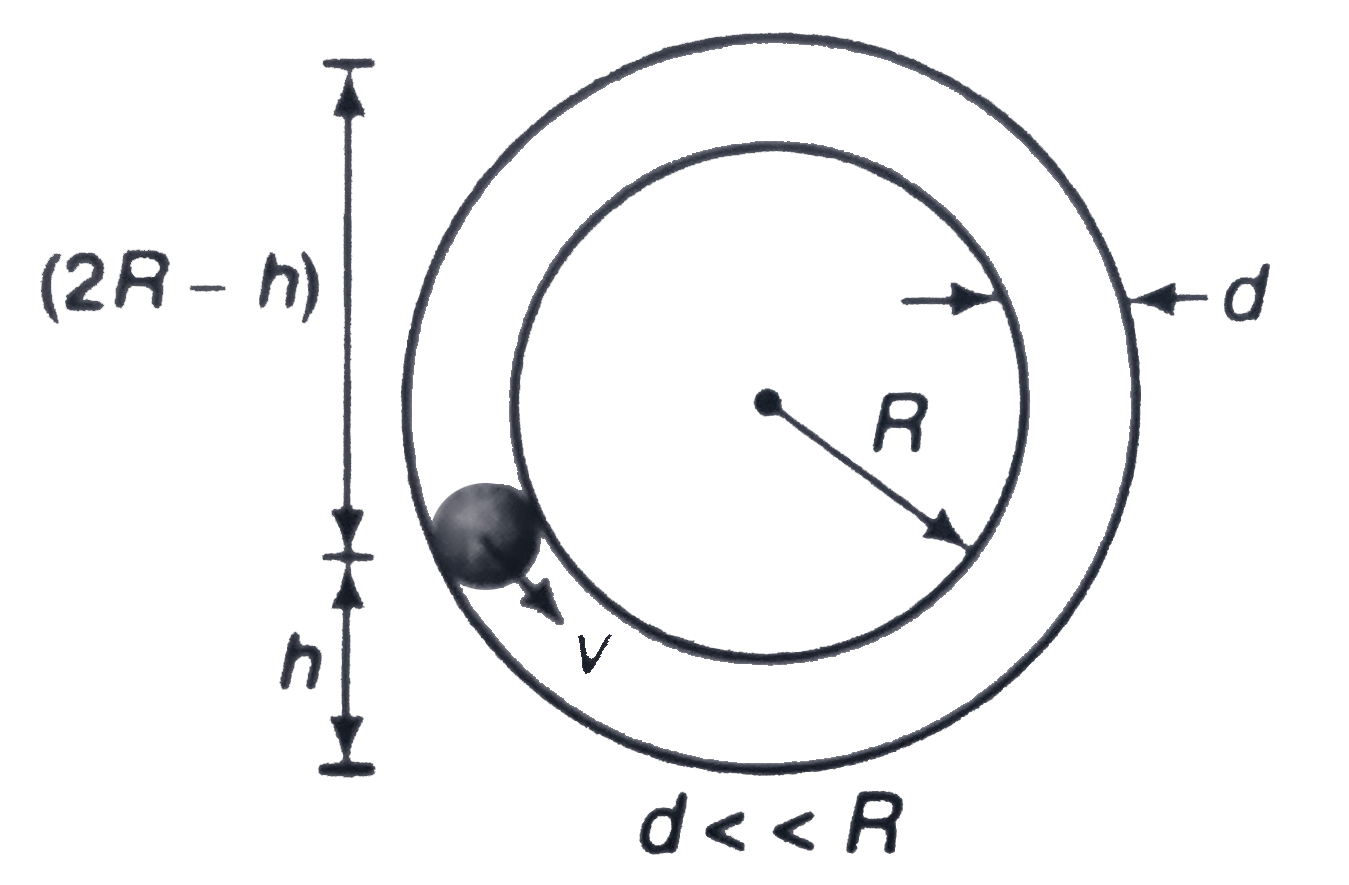
View SolutionWith what minimum speed v must a small ball should be pushed inside a smooth vertical tube from a heoght h so that it may reach the top of the tube? Radius of the tube is R .
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
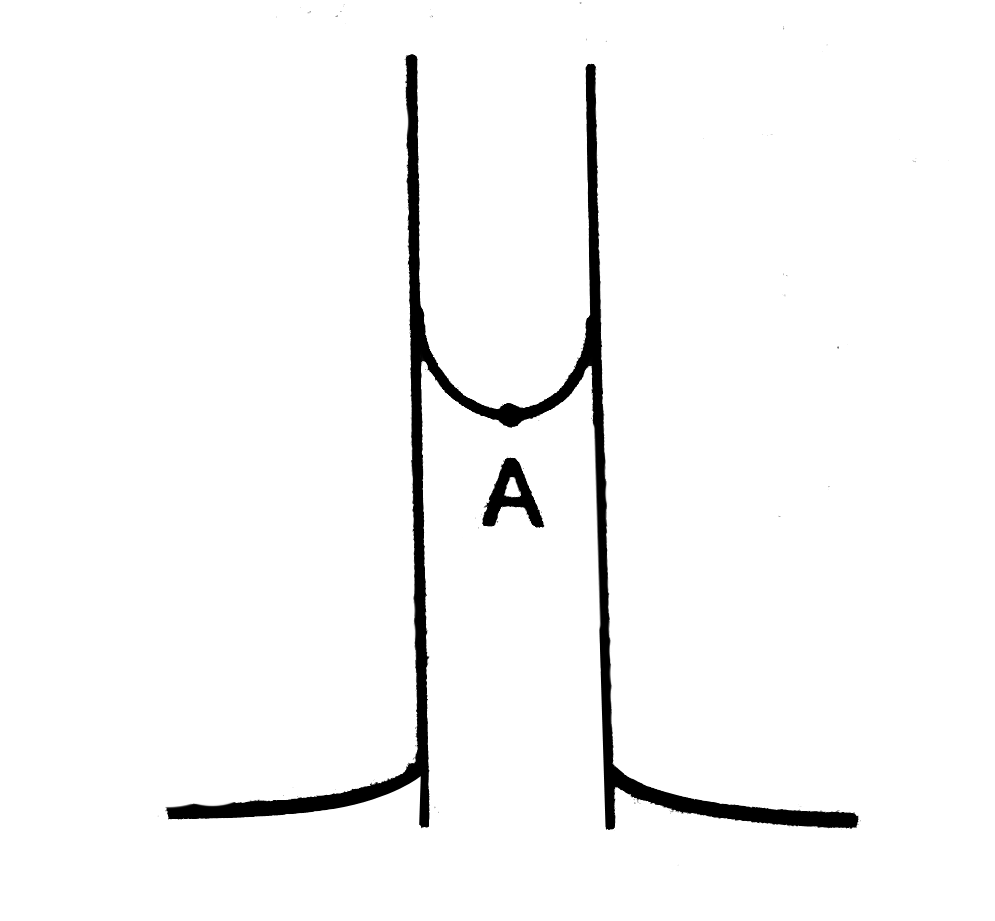
View SolutionA thin uniform copper rod length l and mass m rotates unifomly with an angular velocity ω about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is σmax, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions
The maximum angular velocity with which the rod can rotate so that is won't break, is

View SolutionA circular ring of radius R and mass m made of a uniform wire of cross sectional area A is rotated about a stationary vertical axis passing throgh its centre and perpendicular to the plane of the ring. If the breaking stress of the material of the ring is σb, then determine the maximum angular speed ωmax at which the ring may be rotated without failure.
View Solution

