On applying a stress of xN/m2, the length of wire of some material gets doubled. Value of Young's modulus for the material of wire in N/m2, is (assume Hooke's law to be valid and go for approx. results)
x
2x
x2
Insufficient information
The correct Answer is:A
To solve the problem, we need to find the Young's modulus (Y) of a material given that a wire doubles its length when a stress of xN/m2 is applied. We will use the relationship defined by Hooke's law, which states that Young's modulus is the ratio of stress to strain.
1. Understand the Definitions:
- Stress (σ): It is defined as the force applied per unit area. In this case, it is given as xN/m2.
- Strain (ϵ): It is defined as the change in length divided by the original length.
2. Calculate the Change in Length:
- Let the original length of the wire be l.
- The final length after applying the stress is 2l (since it doubles).
- The change in length (ΔL) is given by:
ΔL=Final Length−Original Length=2l−l=l
3. Calculate the Strain:
- Strain (ϵ) can be calculated as:
ϵ=ΔLl=ll=1
4. Calculate the Young's Modulus:
- Young's modulus (Y) is defined as:
Y=StressStrain=σϵ
- Substituting the values we have:
Y=x1=xN/m2
5. Final Result:
- Therefore, the value of Young's modulus for the material of the wire is:
Y=xN/m2
Summary:
The Young's modulus of the material of the wire is xN/m2.
- Stress (σ): It is defined as the force applied per unit area. In this case, it is given as xN/m2.
- Strain (ϵ): It is defined as the change in length divided by the original length.
- Let the original length of the wire be l.
- The final length after applying the stress is 2l (since it doubles).
- The change in length (ΔL) is given by:
ΔL=Final Length−Original Length=2l−l=l
- Strain (ϵ) can be calculated as:
ϵ=ΔLl=ll=1
- Young's modulus (Y) is defined as:
Y=StressStrain=σϵ
- Substituting the values we have:
Y=x1=xN/m2
- Therefore, the value of Young's modulus for the material of the wire is:
Y=xN/m2
The Young's modulus of the material of the wire is xN/m2.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Subjective
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View SolutionThe young's modulus of a material of wire is 12.6×1011dyne/cm2. Its value is SI system is
View SolutionFind the percentage increase in length of a wire subjected to a stress of 1 gm. Wt /mm2 . Young's modulus of the material of the wire = 100 Gpa.
View SolutionWhat will be the stress required to double the length of a wire of Young's modulus Y?
View SolutionCalculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionA force of one newton doubles the length of a cord having cross-sectional area 1mrh2. The Young's modulus of the material of the cord is
View SolutionA wire of length 15m and diameter 4 mm elongates 0.3mm when stretched by weigth of 2.20kg. Calulate the Young's modulus of the material of the wire.
View SolutionIn the given figure, if the dimensions of the two wires are same but materials are different, then Young's modulus is
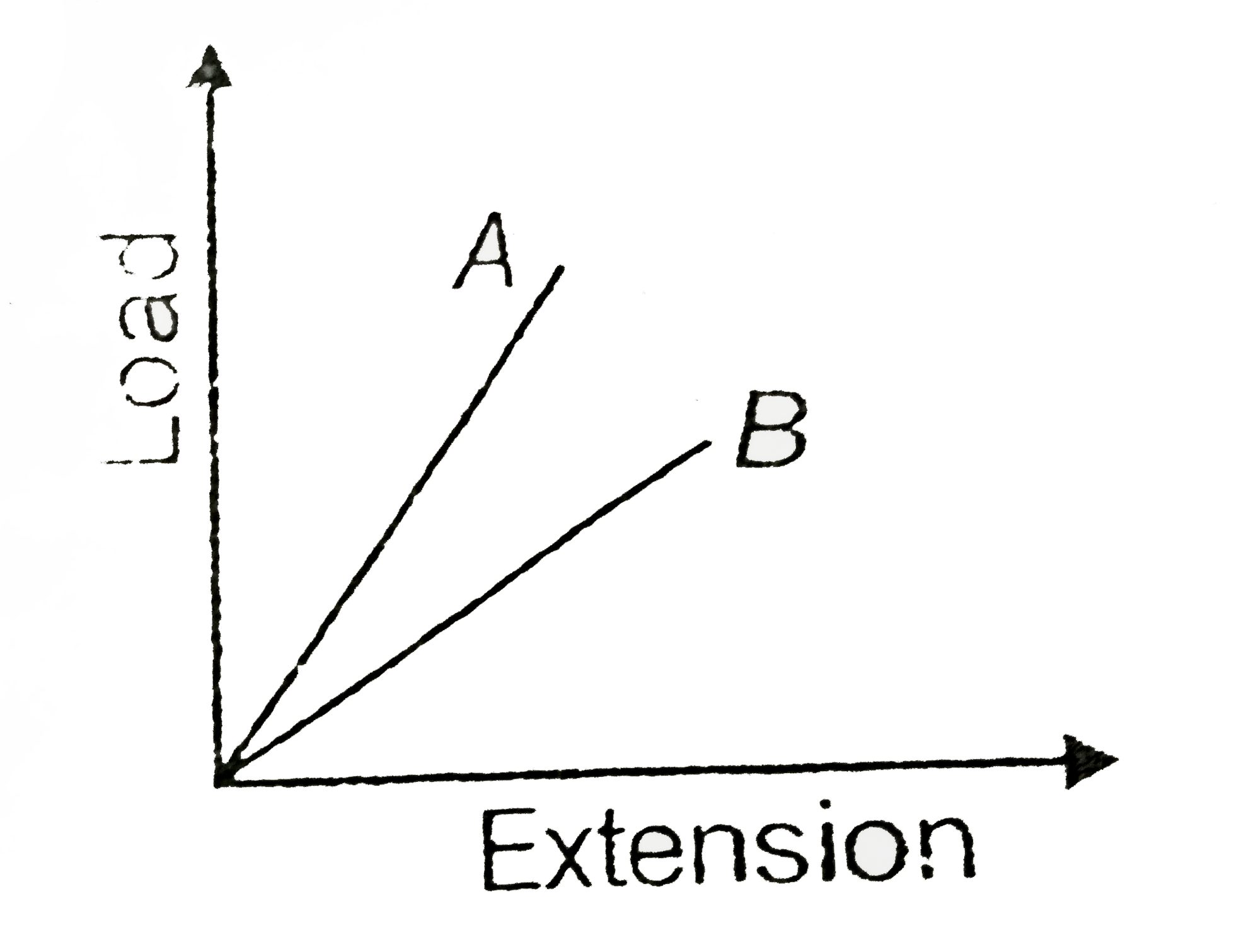
View SolutionIn the given Fig. 7(CF).2, if the dimensions of the two wires are the same and materials are different, Young's modulus is
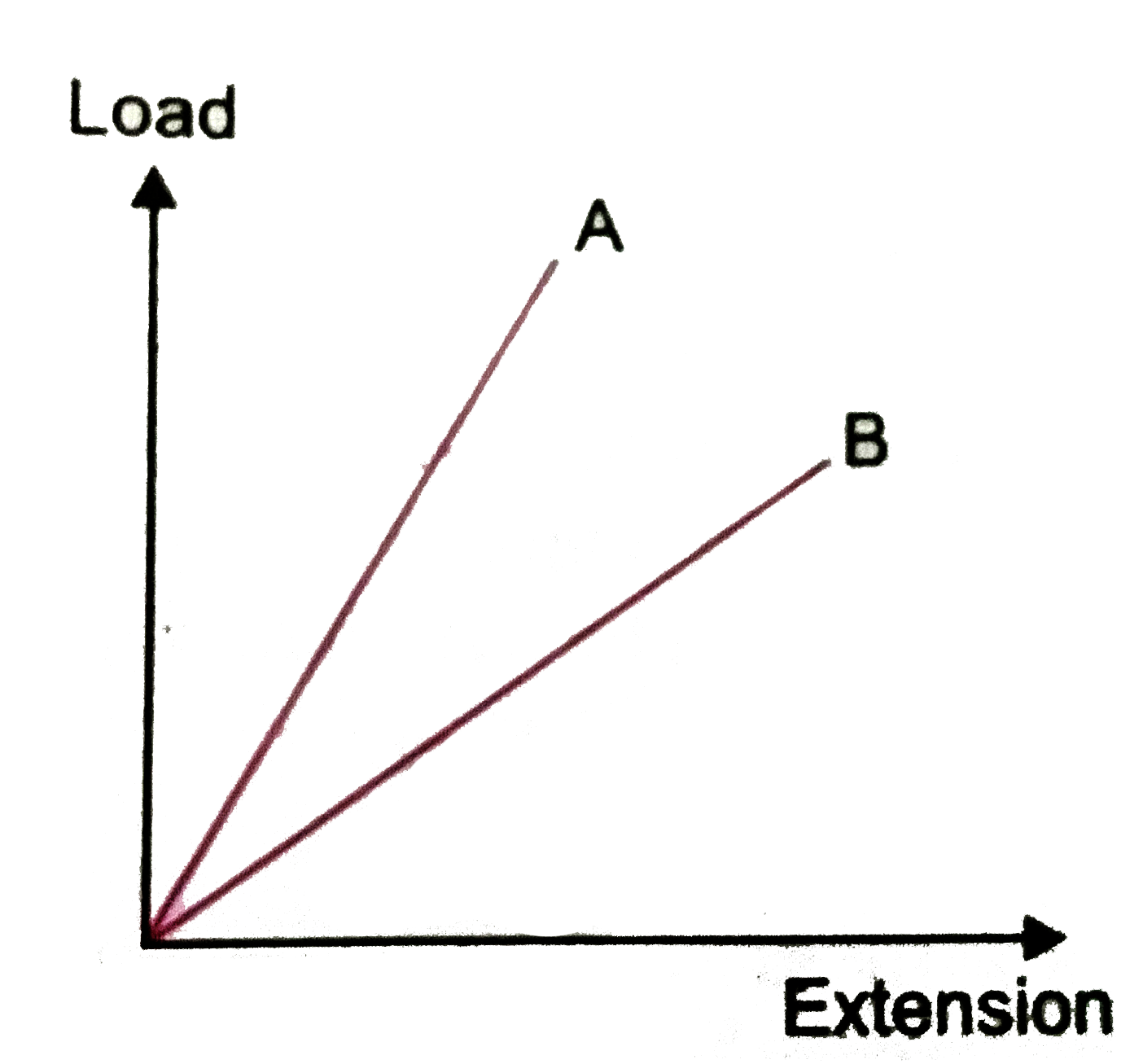
View SolutionThe speed of longitudinal mechanical wave in a material is 4300 m/s. young's modulus of the material is 15×109N/m2. What is the density of the material?
View Solution

