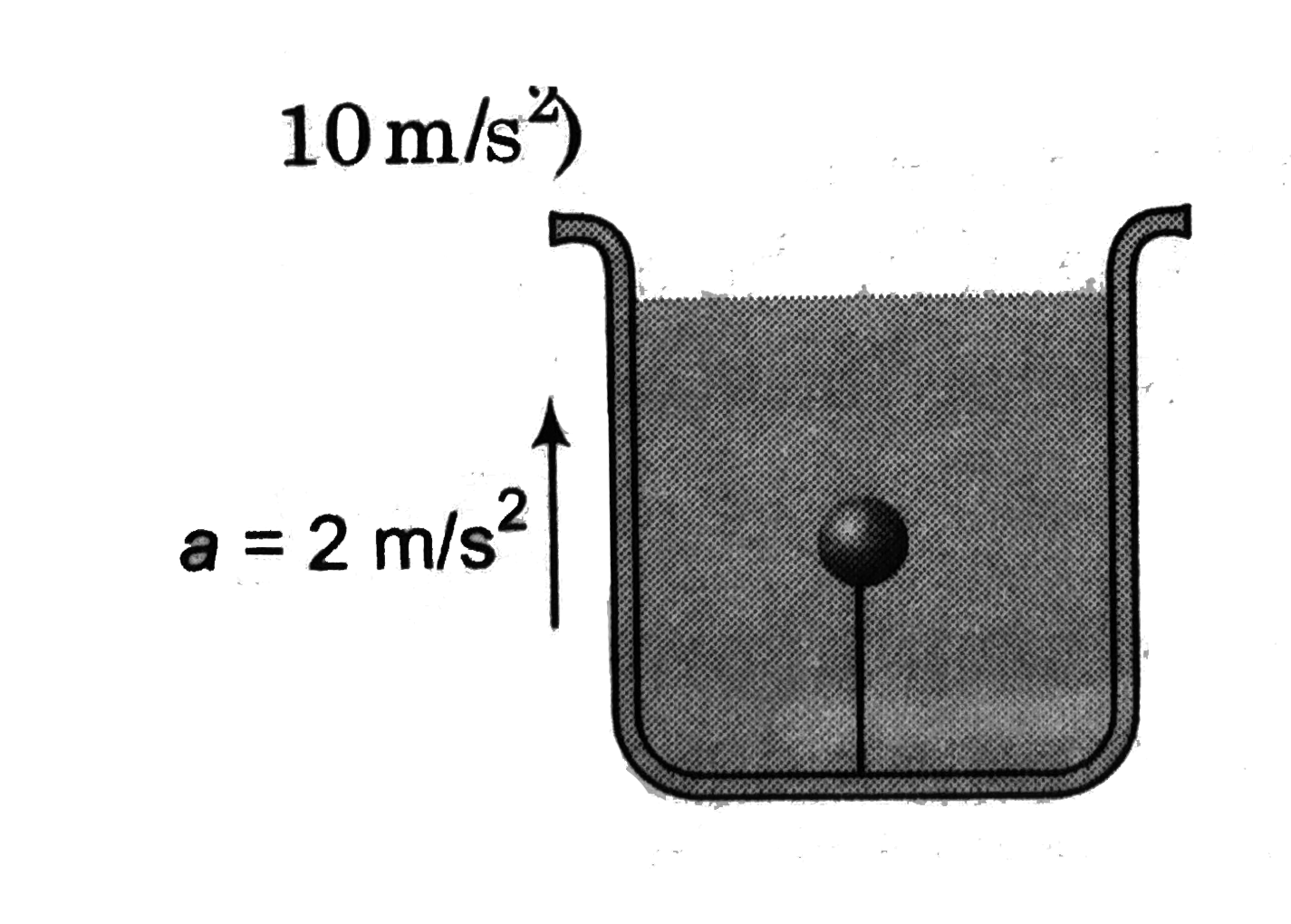
A solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)
Density of the spherical material = specific gravity × density of water =sr
its volme is V=msρ
Hence mass of water displaced by the shere is
Vρ=msρρ=m/s=20.5=4kg
since, the tank is accelerating upwards with acceleration a therefore, apparent value of gravitational acceleration is
g'=g+a=12ms−2
Hence, upthrust exerted by water on the sphere is
F=Vρ(g+a)=48N brgt 
F=mg−T=ma=.T=F−mg−ma=24N
When thread snaps, tension T disappears. Let the sphere now starts accelerating upwards with acceleration b. Considering the free body diagram.
F−mg=mb
∴b=14ms−2
Thus is the absolute acceleration of the sphere. But the tank itself is accelerating upwards with acceleration a. Therefore, upward acceleration of the sphere relative to the tank is b−a=12ms−2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
View SolutionCalculate the molarity of water if its density is 1000kgm−3
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View Solution
