A lift of mass is moving with an acceleration of in upward direction. Tension developed in the string, which is connected to the lift, is.
9800 N
10, 800 N
11000 N
10, 000 N
The correct Answer is:B
To find the tension developed in the string connected to the lift, we can follow these steps:
Step 1: Identify the forces acting on the lift
The forces acting on the lift are:
- The tension (T) in the string acting upwards.
- The weight of the lift (mg) acting downwards, where m is the mass of the lift and g is the acceleration due to gravity.
Step 2: Write the equation of motion
Since the lift is moving upwards with an acceleration (a), we can apply Newton's second law of motion. The net force acting on the lift can be expressed as:
T−mg=ma
Step 3: Substitute the known values
Given:
- Mass of the lift, m=1000kg
- Acceleration due to gravity, g=9.8m/s2
- Acceleration of the lift, a=1m/s2
Now, calculate the weight of the lift:
mg=1000kg×9.8m/s2=9800N
Step 4: Rearrange the equation to solve for tension (T)
From the equation of motion:
T=ma+mg
Step 5: Substitute the values into the equation
Substituting the values we have:
T=(1000kg×1m/s2)+9800N
T=1000N+9800N
T=10800N
Final Answer
The tension developed in the string is T=10800N.
---
The forces acting on the lift are:
- The tension (T) in the string acting upwards.
- The weight of the lift (mg) acting downwards, where m is the mass of the lift and g is the acceleration due to gravity.
Since the lift is moving upwards with an acceleration (a), we can apply Newton's second law of motion. The net force acting on the lift can be expressed as:
T−mg=ma
Given:
- Mass of the lift, m=1000kg
- Acceleration due to gravity, g=9.8m/s2
- Acceleration of the lift, a=1m/s2
mg=1000kg×9.8m/s2=9800N
From the equation of motion:
T=ma+mg
Substituting the values we have:
T=(1000kg×1m/s2)+9800N
T=1000N+9800N
T=10800N
The tension developed in the string is T=10800N.
Similar Questions
A lift of mass 1000 kg which is moving with an acceleration of 1ms−2 in upward direction , then the tension developed in string which is connected to lift is ___________
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View Solution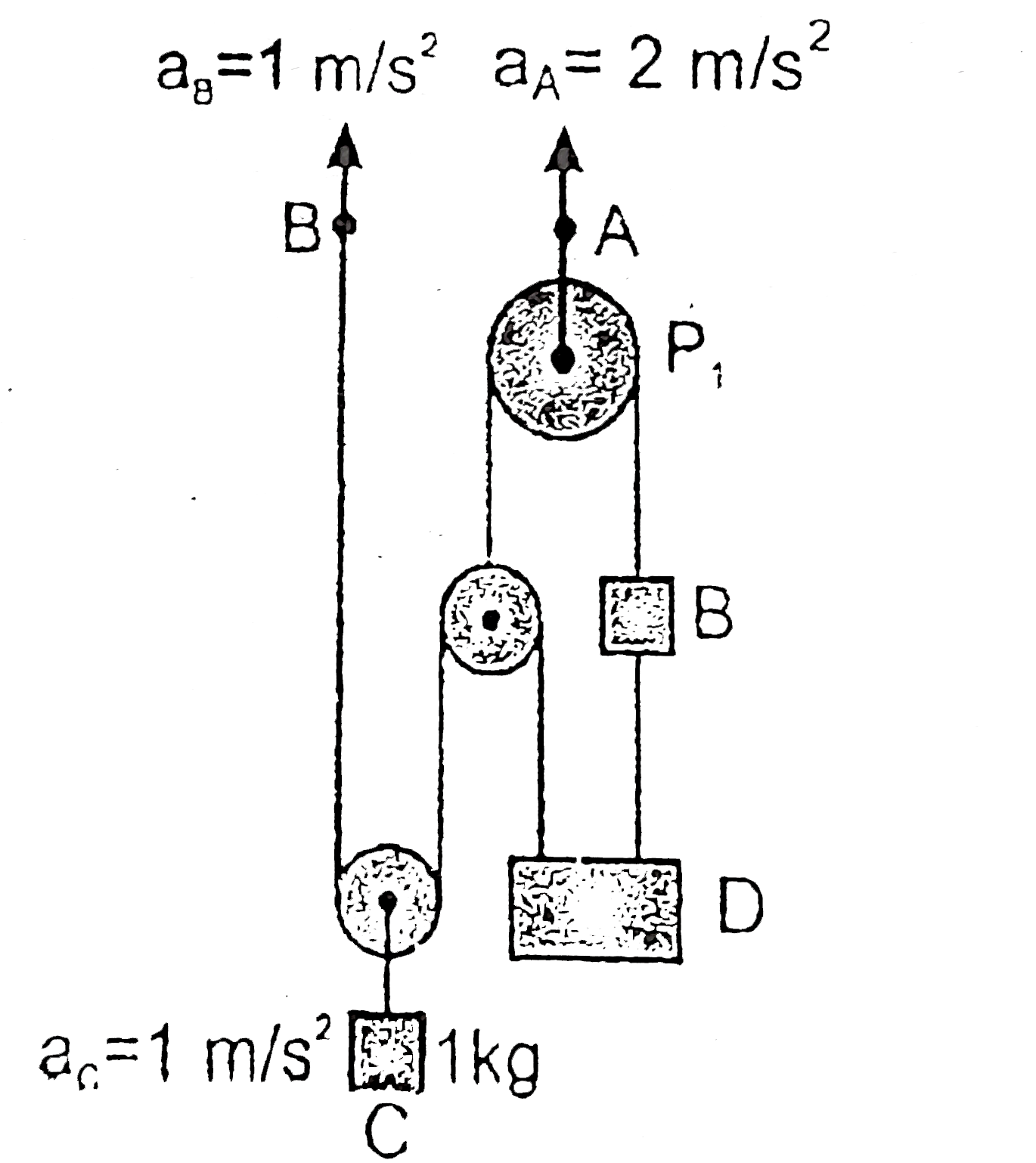
In the arrangement shown in figure pulley and strings are ideal. End A of string connected to pulley P1 is moved upwards with acceleration aA=2m/s2 while end B of another string shown in figure is moved up with acceleration aB=1m/s2. Block C of mass 1 kg is moving up with accelaration 1m/s2. If block D to which string are connected are connected symmetrically moves such that its orientations remains same then (assume g=10m/s2)
View SolutionA lift is moving in upward direction with speed 20m/s and having acceleration 5m/s2 in downward direction. A bolt drops from the ceiling of lift at that moment. Just after the drop, the:
View SolutionThe tension in the cord connected to motor is 15000 N and mass of the lift is 1400 kg. f mass m= 100 kg is inside the connected with a massless string as shown in tigure, then tension in the string connected with m is (g=10ms2)
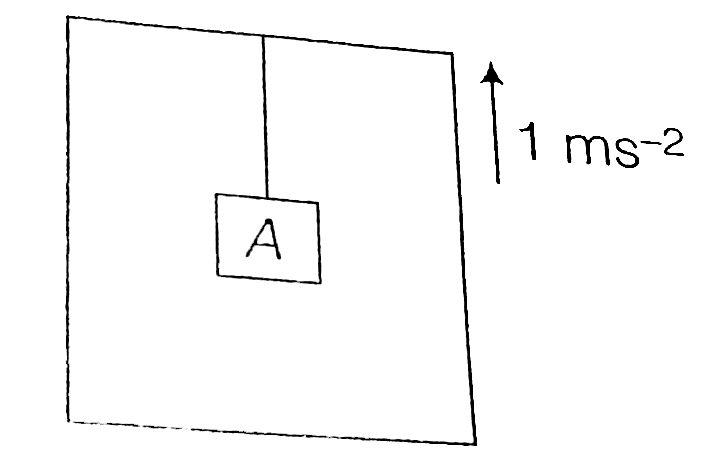
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
View Solution
