A solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.
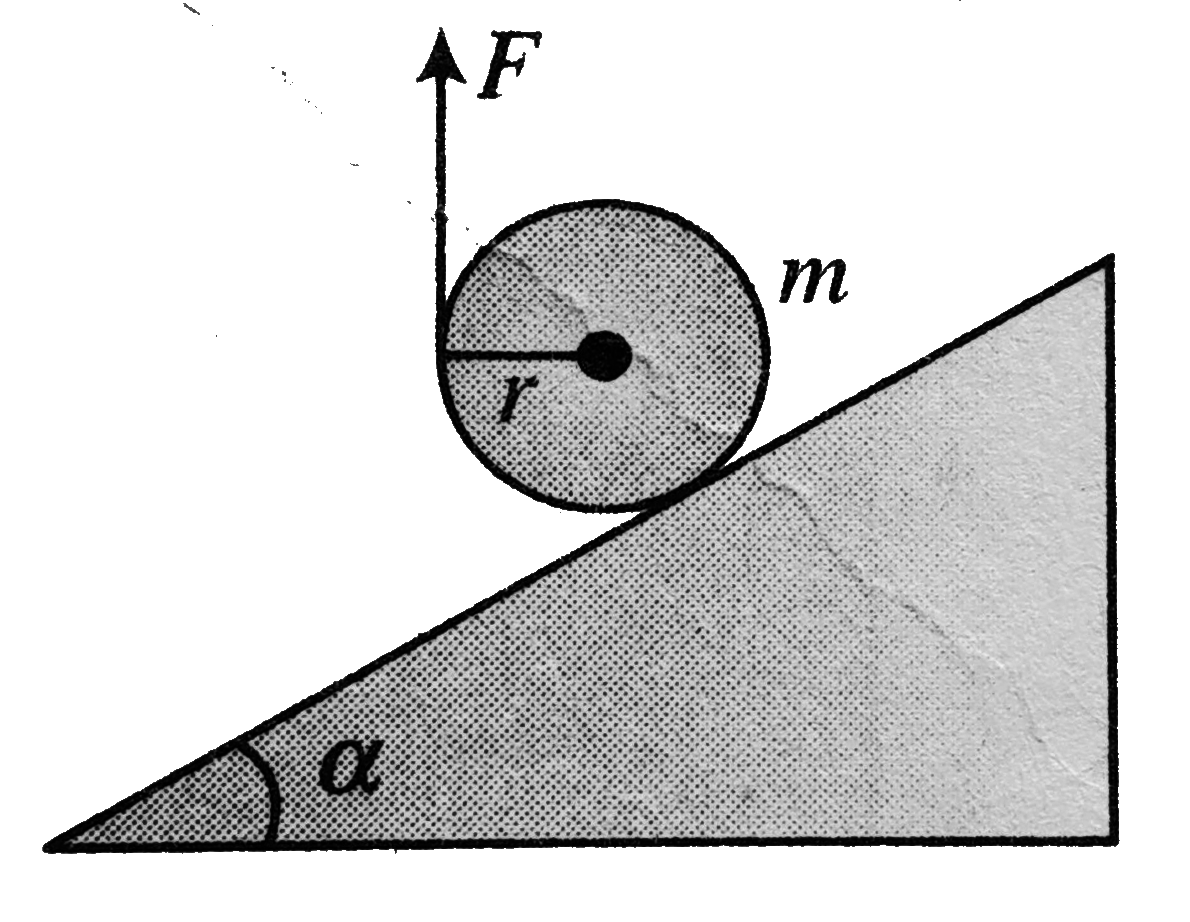
What force F is reqired to kep the cylinder in balance when the thread is held vertically?
mg/2
3mg/4
3mg/8
5mg/8
The correct Answer is:C
Balancing torque about C
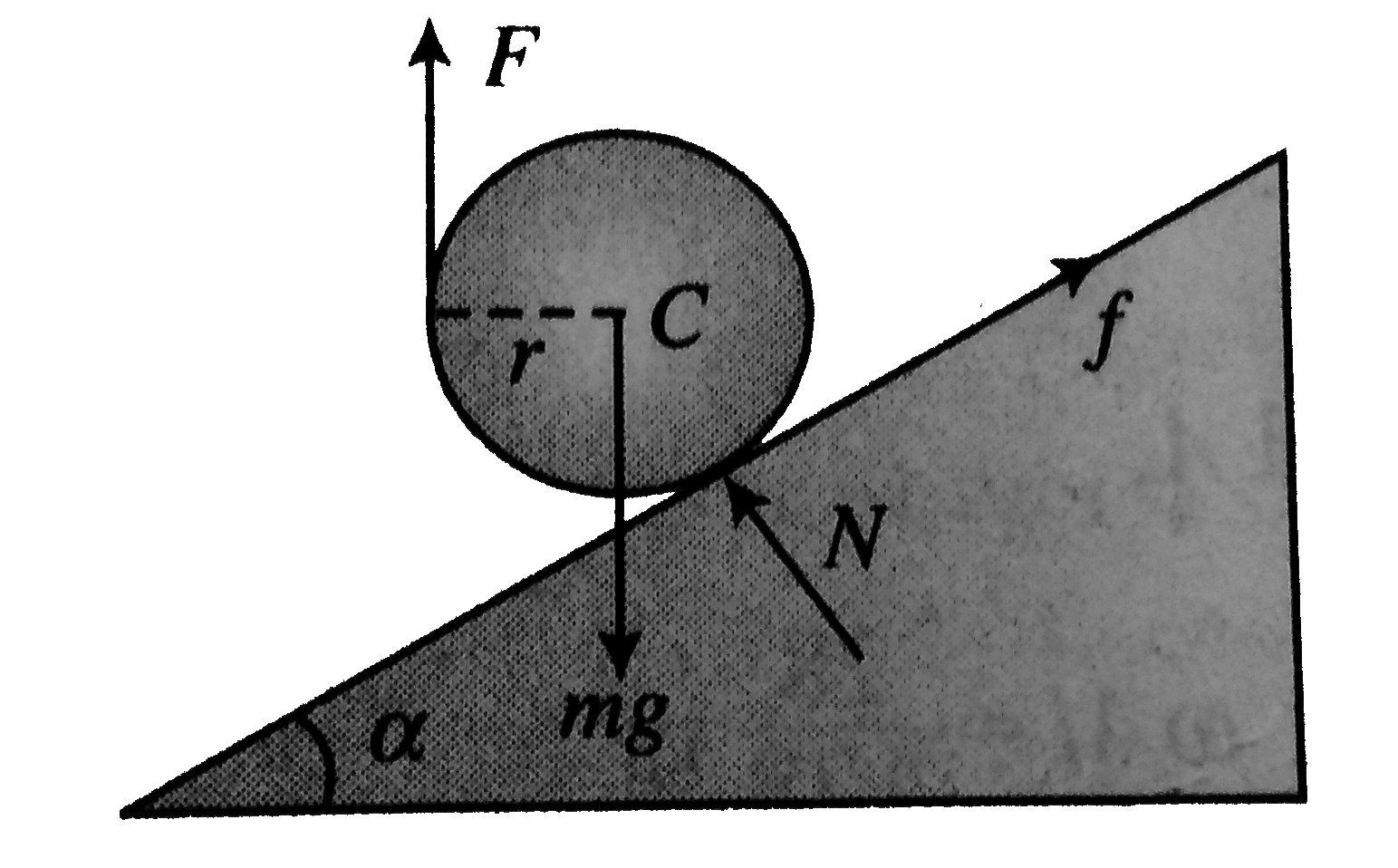
Fr=fr⇒f=F
balancing force in the direction of incline
Fsinα+f=mgsinα
⇒F(35)+F=mg(35)⇒F=3mg8
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

The values of minimum coefficient of static friction between cylinder and incline in the case when F is minimum.
View SolutionA solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

In what direction should the thread be pulled to minimise the force required to hold the cylinder? What is the magnitude of this force?
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
View SolutionA solid cylinder of radius m is kept on an inclined plane on its base and it does not slide. The angle of incline plane is 53∘ with horizontal and it is fixed. What will be maxcimum height (in meters) of the cylinder for it not to topple.
View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
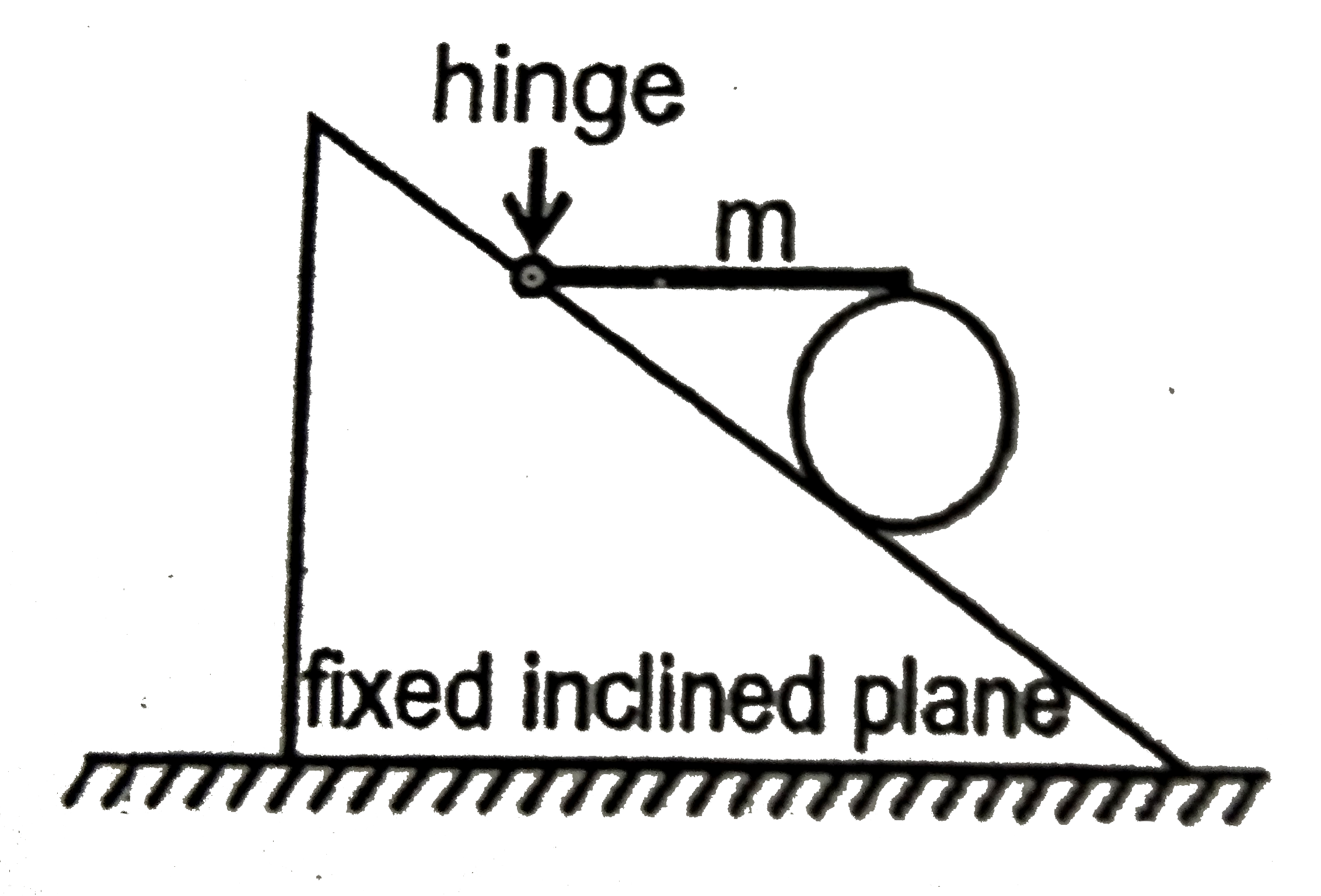
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
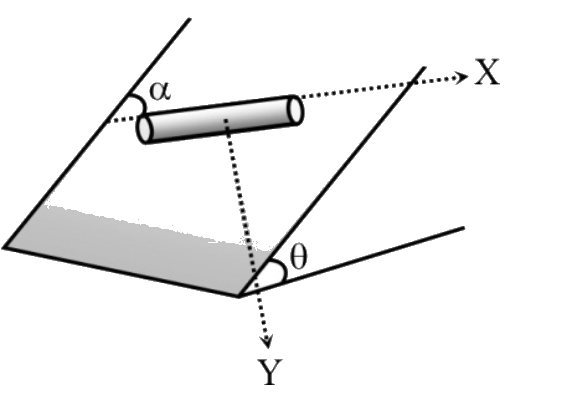
View SolutionA cylinder of mass m is kept on an inclined plane haivng an angle of inclination 30∘. Axis of the cylinder makes an angle 30∘ with the line along the greatest slope. Assuming that cylinder rolls without slipping, the acceleration of the cylinder is
View Solution
