A sphere moving with speed and rotating With angular velocity makes a head-on elastic collision with an identical stationary sphere . There is no friction between the surfaces of and . Choose the conrrect alternative(s). Disregard gravity.
will stop moving but continue to rotate with an angular velocity
will come to rest and stop rotating
will move with speed without rotating
will move with speed and rotate with an angular velocity
The correct Answer is:A, C, D
To solve the problem of the elastic collision between two identical spheres, we will follow these steps:
Step 1: Understand the Initial Conditions
- Sphere A is moving with an initial speed u and has an angular velocity ω.
- Sphere B is stationary (initial speed = 0).
- There is no friction between the surfaces of A and B.
Step 2: Apply Conservation of Linear Momentum
In an elastic collision, the total linear momentum before the collision is equal to the total linear momentum after the collision.
Let:
- m = mass of each sphere
- v1 = final velocity of sphere A after the collision
- v2 = final velocity of sphere B after the collision
Using the conservation of linear momentum:
m⋅u+m⋅0=m⋅v1+m⋅v2
This simplifies to:
u=v1+v2(Equation 1)
Step 3: Apply Conservation of Kinetic Energy
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
The initial kinetic energy is:
KEinitial=12mu2+12IAω2
where IA is the moment of inertia of sphere A, given by IA=25mr2 for a solid sphere.
The final kinetic energy is:
KEfinal=12mv21+12mv22+12IBω2B
Since sphere B is initially stationary and has no rotation, its angular velocity ωB after the collision will be 0.
Setting the initial and final kinetic energies equal gives us:
12mu2+12(25mr2)ω2=12mv21+12mv22
This can be simplified to:
u2+25r2ω2=v21+v22(Equation 2)
Step 4: Solve the Equations
From Equation 1, we have:
v1=u−v2
Substituting v1 into Equation 2:
u2+25r2ω2=(u−v2)2+v22
Expanding and simplifying gives:
u2+25r2ω2=u2−2uv2+2v22
This leads to:
25r2ω2=−2uv2+2v22
Rearranging gives:
2v22−2uv2−25r2ω2=0
Dividing by 2:
v22−uv2−15r2ω2=0
Step 5: Solve for v2
Using the quadratic formula:
v2=u±√u2+45r2ω22
Step 6: Analyze the Results
1. Since there is no friction, sphere A will continue to rotate with the same angular velocity ω.
2. Sphere B will move with speed v2 after the collision, but it will not rotate.
Conclusion
- Sphere A will stop moving linearly but continue to rotate with angular velocity ω.
- Sphere B will move with speed u without any rotation.
- Sphere A is moving with an initial speed u and has an angular velocity ω.
- Sphere B is stationary (initial speed = 0).
- There is no friction between the surfaces of A and B.
In an elastic collision, the total linear momentum before the collision is equal to the total linear momentum after the collision.
- m = mass of each sphere
- v1 = final velocity of sphere A after the collision
- v2 = final velocity of sphere B after the collision
m⋅u+m⋅0=m⋅v1+m⋅v2
This simplifies to:
u=v1+v2(Equation 1)
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
KEinitial=12mu2+12IAω2
where IA is the moment of inertia of sphere A, given by IA=25mr2 for a solid sphere.
KEfinal=12mv21+12mv22+12IBω2B
Since sphere B is initially stationary and has no rotation, its angular velocity ωB after the collision will be 0.
12mu2+12(25mr2)ω2=12mv21+12mv22
This can be simplified to:
u2+25r2ω2=v21+v22(Equation 2)
From Equation 1, we have:
v1=u−v2
Substituting v1 into Equation 2:
u2+25r2ω2=(u−v2)2+v22
Expanding and simplifying gives:
u2+25r2ω2=u2−2uv2+2v22
This leads to:
25r2ω2=−2uv2+2v22
Rearranging gives:
2v22−2uv2−25r2ω2=0
Dividing by 2:
v22−uv2−15r2ω2=0
Using the quadratic formula:
v2=u±√u2+45r2ω22
1. Since there is no friction, sphere A will continue to rotate with the same angular velocity ω.
2. Sphere B will move with speed v2 after the collision, but it will not rotate.
- Sphere A will stop moving linearly but continue to rotate with angular velocity ω.
- Sphere B will move with speed u without any rotation.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Particle A makes a head on elastic collision with another stationary particle B. They fly apart in opposite directions with equal speeds. The mass ratio will be
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
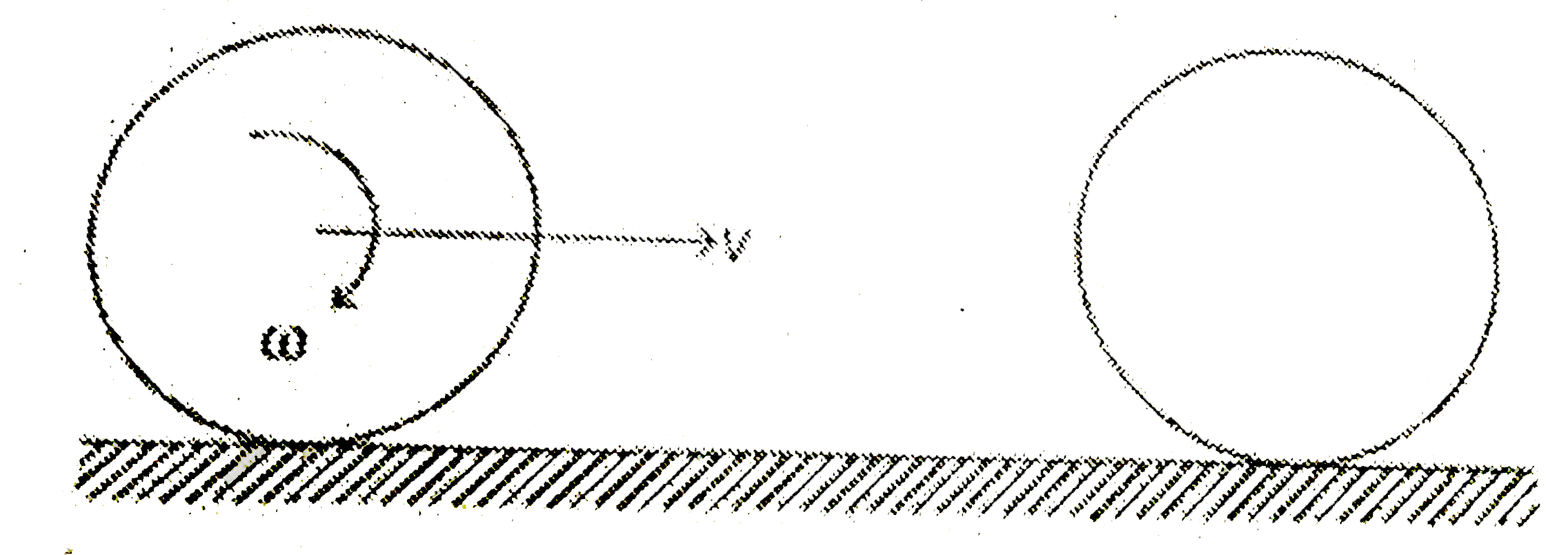
What is the net angular impulse imparted to second sphere by the external forces?
View Solution
Knowledge Check
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘
A solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
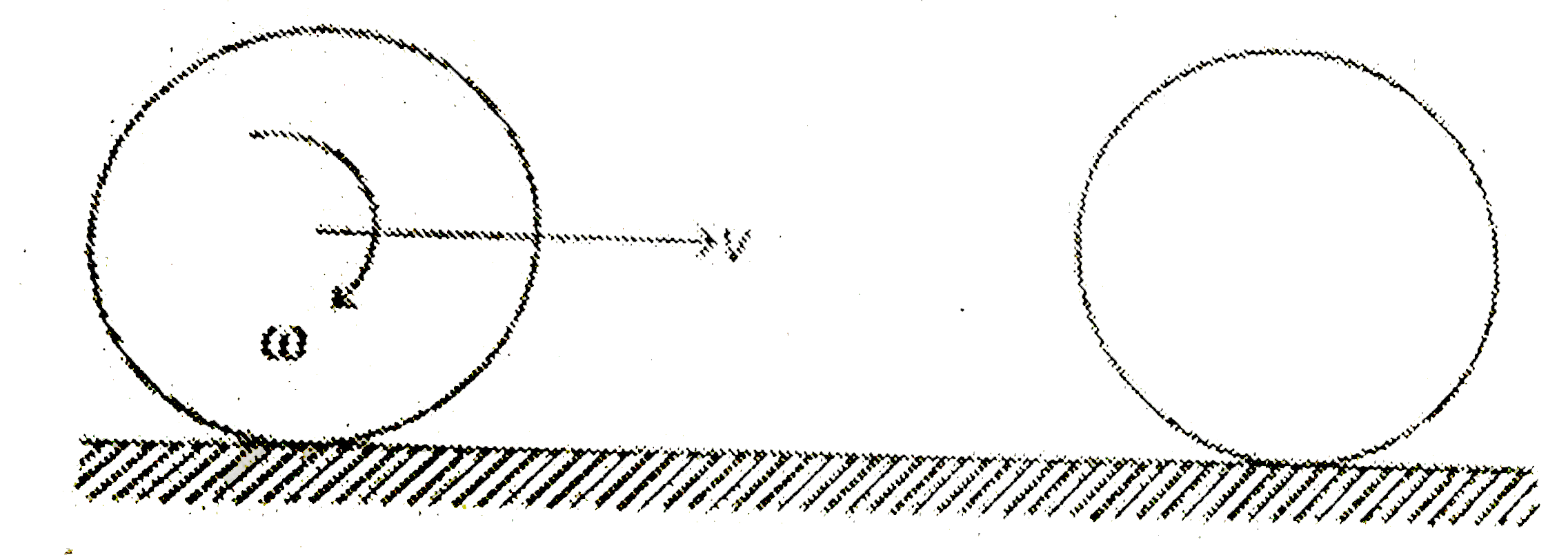
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
View SolutionIf a sphere of mass m moving with velocity u collides with another identical sphere at rest on a frictionless surface, then which of the following is correct ?
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move

View SolutionA moving sphere of mass m suffer a perfect elastic collision (not head on) with equally massive stationary sphere. After collision both fly off at angle θ, value of which is :
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
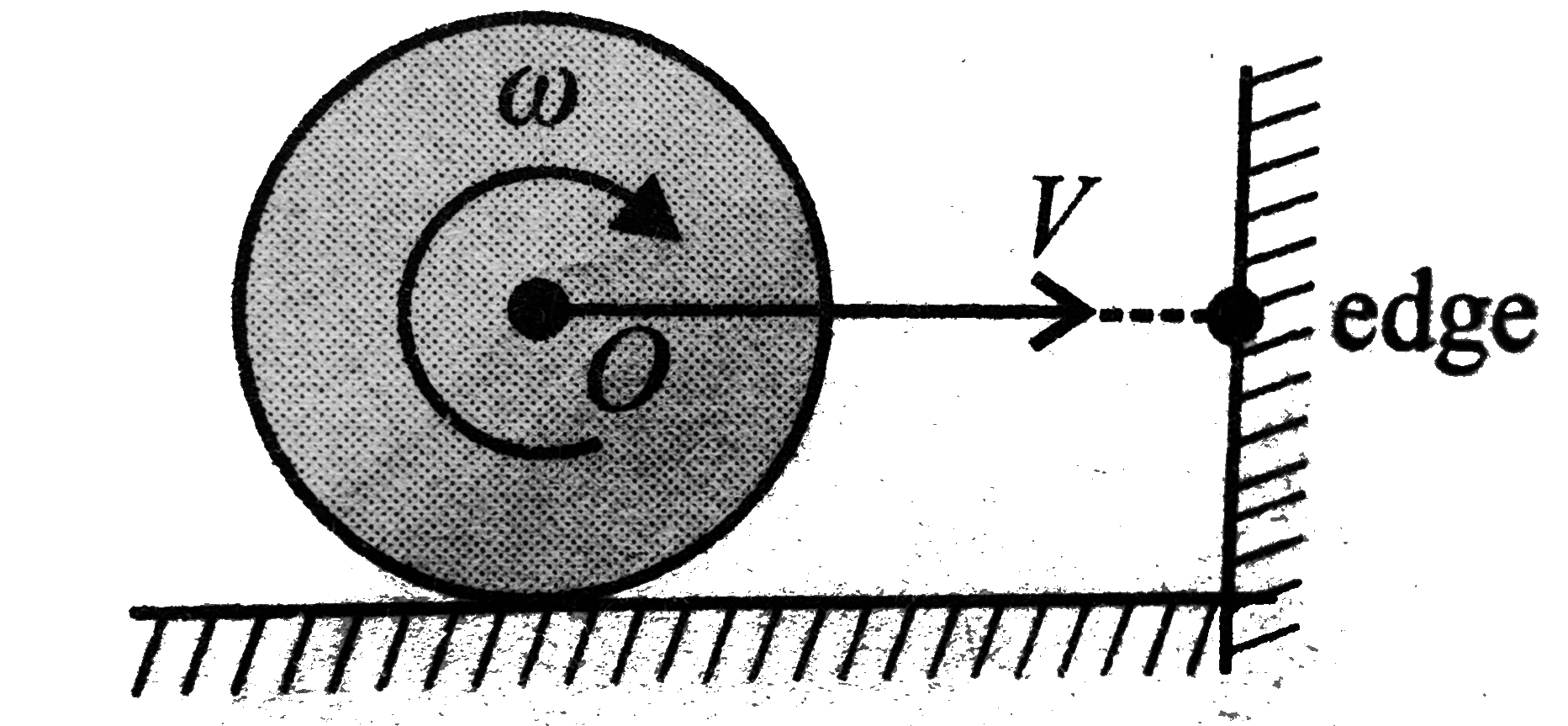
View Solution
