A particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
Velocity of centre of mass (CM) is 5ˆims−1
The velocities of the particles relative to the centre of mass have same magnitude.
Speed of individual particle before and after collision remains same.
The velocity of particles relative to CM after collision are →v1f/cm=−ˆims−1,→v2f/cm=2ˆims−1
The correct Answer is:A, D

vcm=4×6+2×34+2=5ms−1
u1cm=u1−vcm=6−5=1ms−1
v2cm=u1−vcm=6−5=1ms−1
v2cm=u1−vcm=4−5=−1ms−1
Here b in incorrect.
After collision : v1=4ms−1,v2=7ms−1
v2cm=v2−vcm=7−5=2ms−1
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension105videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct141videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A partical of mass m moving with velocity 1m/s collides perfectly elastically with another particle of mass 2m. If the incident particle is deflected by 90∘. The heavy mass will make and angle θ with the initial direction of m equal to:
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass 1 g moving with a velocity →v1=3ˆi−2ˆjms−1 experiences a perfectly in elastic collision with another particle of mass 2 g and velocity →v2=4ˆj−6ˆkms−1. The velocity of the particle is
View SolutionA particle of mass 2 kg moving with a speed of 6 m/s collides elastically with another particle of mass 4 kg travelling in same direction with a speed of 2m/s. The maximum possible deflection of the 2 kg particle is
View SolutionA particle of mass m and momentum p moves on a smooth horizontal table and collides directly and elastically with a similar particle (of mass m) having momentum −2p. The loss (−) or gain (+) in the kinetic energy of the first particle in the collision is
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
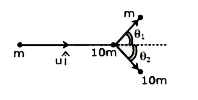 View Solution
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View Solution


