A particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
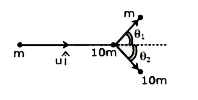
The correct Answer is:10
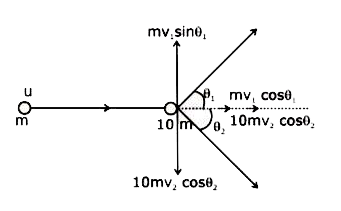
12mv21=12(12mu2)
v21=u22
v1=u√2 ….(i)
Also , 12mu2=12mv21+12(10m)×v22
12×10m×v22=12×12mu2
v22=u220 or , v2=u√20
now , mv1sinθ1=10mv2sinθ2
u√2sinθ1=10×u√20sinθ2
sinθ1=10√10sinθ2
sinθ1=√10sinθ2
∴n=10
Topper's Solved these Questions
Similar Questions
A particle of mass m with an initial velocity uˆi collides perfectly elastically with a mass 3 m at rest . It moves with a velocity vˆj after collision , then , v is given by :
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA particle of mass m travelling with velocity v and kinetic energy E collides elastically to another particle of mass nm, at rest. What is the fraction of total energy retained by the particle of mass m?
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
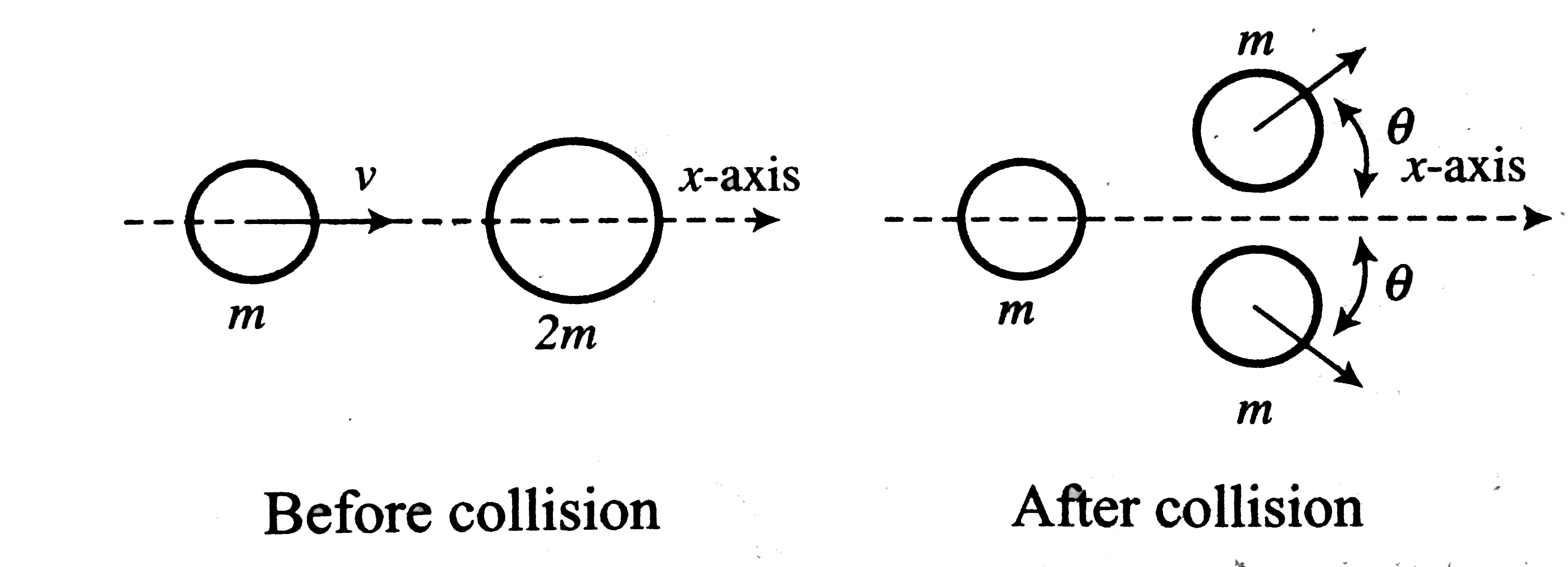
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View Solution
