A particle of mass m and momentum p moves on a smooth horizontal table and collides directly and elastically with a similar particle (of mass m) having momentum −2p. The loss (−) or gain (+) in the kinetic energy of the first particle in the collision is
(a) +p22m
(b) −p24m
(c) +3p22m
(d) zero
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the given data
We have two particles, both with mass m. The first particle has momentum p, and the second particle has momentum −2p.
Step 2: Calculate the velocities of the particles
Using the formula for momentum p=mv, we can find the velocities of both particles.
- For the first particle:
p=mv1⟹v1=pm
- For the second particle:
−2p=mv2⟹v2=−2pm
Step 3: Calculate the initial kinetic energies
The kinetic energy KE of a particle is given by the formula:
KE=12mv2
- For the first particle:
KE1=12m(pm)2=12m⋅p2m2=p22m
- For the second particle:
KE2=12m(−2pm)2=12m⋅4p2m2=2p2m
Step 4: Calculate the total initial kinetic energy
The total initial kinetic energy KEinitial is the sum of the kinetic energies of both particles:
KEinitial=KE1+KE2=p22m+2p2m=p22m+4p22m=5p22m
Step 5: Analyze the elastic collision
In an elastic collision between two equal masses, the velocities are exchanged. Thus, after the collision:
- The first particle will have the velocity of the second particle v2.
- The second particle will have the velocity of the first particle v1.
- After the collision, the velocity of the first particle becomes v2=−2pm.
Step 6: Calculate the final kinetic energy of the first particle
Now we calculate the kinetic energy of the first particle after the collision:
KEfinal=12m(−2pm)2=12m⋅4p2m2=2p2m
Step 7: Calculate the change in kinetic energy
The change in kinetic energy ΔKE for the first particle is given by:
ΔKE=KEfinal−KEinitial=2p2m−p22m
To combine these:
ΔKE=4p22m−p22m=3p22m
Step 8: Determine if it is a gain or loss
Since ΔKE is positive, it indicates a gain in kinetic energy.
Final Answer
The gain in kinetic energy of the first particle in the collision is:
3p22m
We have two particles, both with mass m. The first particle has momentum p, and the second particle has momentum −2p.
Using the formula for momentum p=mv, we can find the velocities of both particles.
p=mv1⟹v1=pm
−2p=mv2⟹v2=−2pm
The kinetic energy KE of a particle is given by the formula:
KE=12mv2
KE1=12m(pm)2=12m⋅p2m2=p22m
KE2=12m(−2pm)2=12m⋅4p2m2=2p2m
The total initial kinetic energy KEinitial is the sum of the kinetic energies of both particles:
KEinitial=KE1+KE2=p22m+2p2m=p22m+4p22m=5p22m
In an elastic collision between two equal masses, the velocities are exchanged. Thus, after the collision:
- The first particle will have the velocity of the second particle v2.
- The second particle will have the velocity of the first particle v1.
Now we calculate the kinetic energy of the first particle after the collision:
KEfinal=12m(−2pm)2=12m⋅4p2m2=2p2m
The change in kinetic energy ΔKE for the first particle is given by:
ΔKE=KEfinal−KEinitial=2p2m−p22m
ΔKE=4p22m−p22m=3p22m
Since ΔKE is positive, it indicates a gain in kinetic energy.
The gain in kinetic energy of the first particle in the collision is:
3p22m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct Option
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 More Than One Correct
8 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Knowledge Check
For a moving particle (mass m, velocity v) having a momentum p, which one of the following correctly describes the kinetic energy of the particle?
Ap22mBp2mCv22mDv2m
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
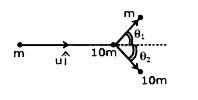
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View Solution
