A steel ball of mass 0.5kg is fastened to a cord 20cm long and fixed at the far end and is released when the cord is horizontal. At the bottom of its path the ball strikes a 2.5kg steel block initially at rest on a frictionless surface. The collision is elastic. The speed of the block just after the collision will be.
a.103ms−1
b. 203ms−1
c. 5ms−1
d. 53ms−1
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Determine the speed of the steel ball just before the collision
When the steel ball is released from the horizontal position, it converts its potential energy at the height of the cord into kinetic energy at the bottom of its swing.
1. Potential Energy (PE) at the top:
PE=mgh
where:
- m=0.5kg (mass of the ball)
- g=9.8m/s2 (acceleration due to gravity)
- h=0.2m (height, which is the length of the cord)
PE=0.5×9.8×0.2=0.98J
2. Kinetic Energy (KE) at the bottom:
KE=12mv2
Setting PE=KE:
0.98=12×0.5×v2
0.98=0.25v2⟹v2=0.980.25=3.92⟹v=√3.92≈1.98m/s
Step 2: Apply conservation of momentum
In an elastic collision, the momentum before the collision equals the momentum after the collision.
Let:
- m1=0.5kg (mass of the ball)
- m2=2.5kg (mass of the block)
- u1=1.98m/s (initial speed of the ball)
- u2=0m/s (initial speed of the block)
- v1 = final speed of the ball after collision
- v2 = final speed of the block after collision
Using conservation of momentum:
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
0.5×1.98+2.5×0=0.5v1+2.5v2
0.99=0.5v1+2.5v2(1)
Step 3: Apply conservation of kinetic energy
In an elastic collision, the total kinetic energy before the collision equals the total kinetic energy after the collision.
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the known values:
12×0.5×(1.98)2+0=12×0.5v21+12×2.5v22
0.5×0.5×3.92=0.25v21+1.25v22
0.98=0.25v21+1.25v22(2)
Step 4: Solve the equations
From equation (1):
0.5v1+2.5v2=0.99⟹v1=0.99−2.5v20.5=1.98−5v2
Substituting v1 in equation (2):
0.98=0.25(1.98−5v2)2+1.25v22
This is a quadratic equation in terms of v2. Solving this will give us the value of v2.
Step 5: Calculate v2
After substituting and simplifying, you will find:
v2≈23m/s
Final Answer
The speed of the block just after the collision is approximately 23m/s.
---
PE=mgh
where:
- m=0.5kg (mass of the ball)
- g=9.8m/s2 (acceleration due to gravity)
- h=0.2m (height, which is the length of the cord)
KE=12mv2
Setting PE=KE:
0.98=12×0.5×v2
0.98=0.25v2⟹v2=0.980.25=3.92⟹v=√3.92≈1.98m/s
- m1=0.5kg (mass of the ball)
- m2=2.5kg (mass of the block)
- u1=1.98m/s (initial speed of the ball)
- u2=0m/s (initial speed of the block)
- v1 = final speed of the ball after collision
- v2 = final speed of the block after collision
m1u1+m2u2=m1v1+m2v2
Substituting the known values:
0.5×1.98+2.5×0=0.5v1+2.5v2
0.99=0.5v1+2.5v2(1)
Substituting the known values:
12×0.5×(1.98)2+0=12×0.5v21+12×2.5v22
0.5×0.5×3.92=0.25v21+1.25v22
0.98=0.25v21+1.25v22(2)
0.5v1+2.5v2=0.99⟹v1=0.99−2.5v20.5=1.98−5v2
0.98=0.25(1.98−5v2)2+1.25v22
v2≈23m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A buttle weighting 10 g and moving with a velocity 800ms−1 strikes a 10 kg block resting on a frictionless surface. The speed of the block after the perfectly inelastic collision is approximately
View SolutionA bullet weighing 10 g and moving with a velocity 300 m/s strikes a 5 kg block of ice and drop dead. The ice block is kept on smooth surface. The speed of the block after the the collision is
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionTwo balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.

View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of 0.5m/s. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is 30cm/s.
View SolutionThree identical block A, B and C are placed on a horizontal frictionless surface. The blocks B and C are at rest but A is approaching towards B with a speed 10ms−1. The coefficient of restitution for all collisions is 0.5. The speed of the block C just after the collision is

View SolutionThree identical blocks A, B and C are placed on horizontal frictionless surface. The blocks B and C are at rest. But A is approaching towards B with a speed of 10ms−1
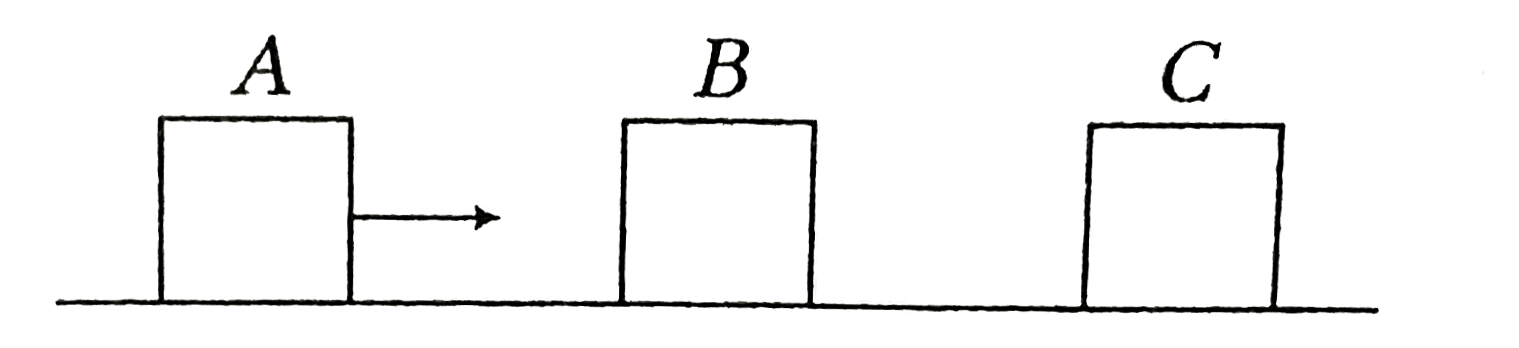
The coefficient of restitution for all collision is 0.5. The speed of the block C just after collision is
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :
View Solution
