Two identical carts constrained to move on a straight line, on which sit two twins of same mass, are moving with equal velocity. At some time snow begins to drop uniformly. Ram, sitting on one of the carts, picks the snow from cart and throws off the falling snow sideways and in the second cart Shyam is asleep.
Cart carrying Ram will have more speed finally than that carrying Shyam.
Cart carrying Ram will have less speed finally than that carrying Shyam.
Cart carrying Ram will have same speed finally than that carrying Shyam.
depends on the amount of snow thrown.
The correct Answer is:D
To solve the problem, we need to analyze the situation involving the two identical carts, the twins Ram and Shyam, and the snow that Ram throws off the cart.
1. Understanding the System:
- We have two identical carts moving with the same velocity.
- Ram is on one cart and Shyam is on the other cart.
- Snow begins to fall uniformly, and Ram picks up the snow and throws it off sideways.
2. Analyzing the Motion:
- Since both carts are identical and moving with the same initial velocity, we can denote their initial velocities as v.
- When Ram throws the snow sideways, we need to consider the conservation of momentum.
3. Effect of Throwing Snow:
- When Ram throws the snow sideways, he exerts a force on the snow, which will impart a momentum to the snow in the sideways direction.
- However, since the snow is thrown sideways and not in the direction of the cart's motion, it does not affect the forward momentum of the cart significantly.
4. Conservation of Momentum:
- The total momentum of the system (both carts and the snow) before Ram throws the snow must equal the total momentum after he throws it.
- Since the snow is thrown sideways, the momentum in the direction of the cart's motion remains unchanged.
5. Final Velocities:
- After Ram throws the snow, the cart he is on (let's call it Cart A) will continue to move with the same velocity v because the sideways throw does not change the forward momentum.
- The cart with Shyam (Cart B) remains unaffected and continues to move with the same velocity v as well.
6. Conclusion:
- Both carts will continue to move with the same velocity after Ram throws the snow. Therefore, the final velocities of both carts are equal.
Final Answer:
The final velocities of both carts (Carrying Ram and Shyam) will remain the same after Ram throws the snow sideways.
---
- We have two identical carts moving with the same velocity.
- Ram is on one cart and Shyam is on the other cart.
- Snow begins to fall uniformly, and Ram picks up the snow and throws it off sideways.
- Since both carts are identical and moving with the same initial velocity, we can denote their initial velocities as v.
- When Ram throws the snow sideways, we need to consider the conservation of momentum.
- When Ram throws the snow sideways, he exerts a force on the snow, which will impart a momentum to the snow in the sideways direction.
- However, since the snow is thrown sideways and not in the direction of the cart's motion, it does not affect the forward momentum of the cart significantly.
- The total momentum of the system (both carts and the snow) before Ram throws the snow must equal the total momentum after he throws it.
- Since the snow is thrown sideways, the momentum in the direction of the cart's motion remains unchanged.
- After Ram throws the snow, the cart he is on (let's call it Cart A) will continue to move with the same velocity v because the sideways throw does not change the forward momentum.
- The cart with Shyam (Cart B) remains unaffected and continues to move with the same velocity v as well.
- Both carts will continue to move with the same velocity after Ram throws the snow. Therefore, the final velocities of both carts are equal.
The final velocities of both carts (Carrying Ram and Shyam) will remain the same after Ram throws the snow sideways.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two boats A and B moved away from a buoy anchored in the middle of a river along the mutually perpendicular straight lines. A moved along the river and B at fight angle to it Having moves off equal distances from the boy, the boats returned. Find the ratio of the times of motion of the boats, if the velocity of each boat with respect to still water in η=1.2 times greater than the velocity of water current.
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionTwo bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of 40ms−1, and the second starts from rest with a constant acceleration of 4ms−2.Find the time that elapses before the second catches the first body. Find the also the greatest distance between them prior to it and time at which this occurs.
View SolutionTwo particles A and B starts from rest and move for equal time on a straight line. The particle A has an acceleration a for the first half of the total time and 2a for the second half. The particle B has an acceleration 2a for the first half and a for the second half. Which particle has covered larger distance?
View Solution
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
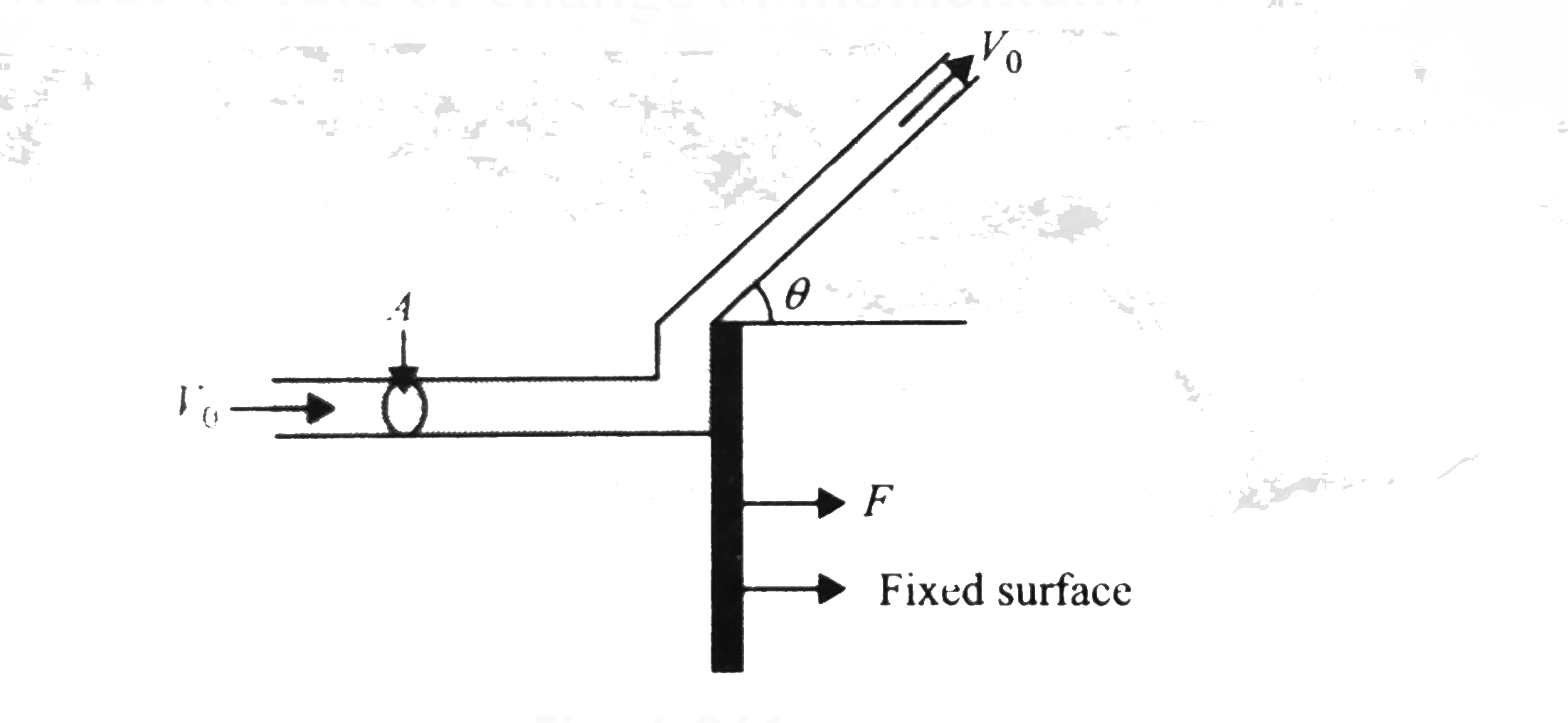
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
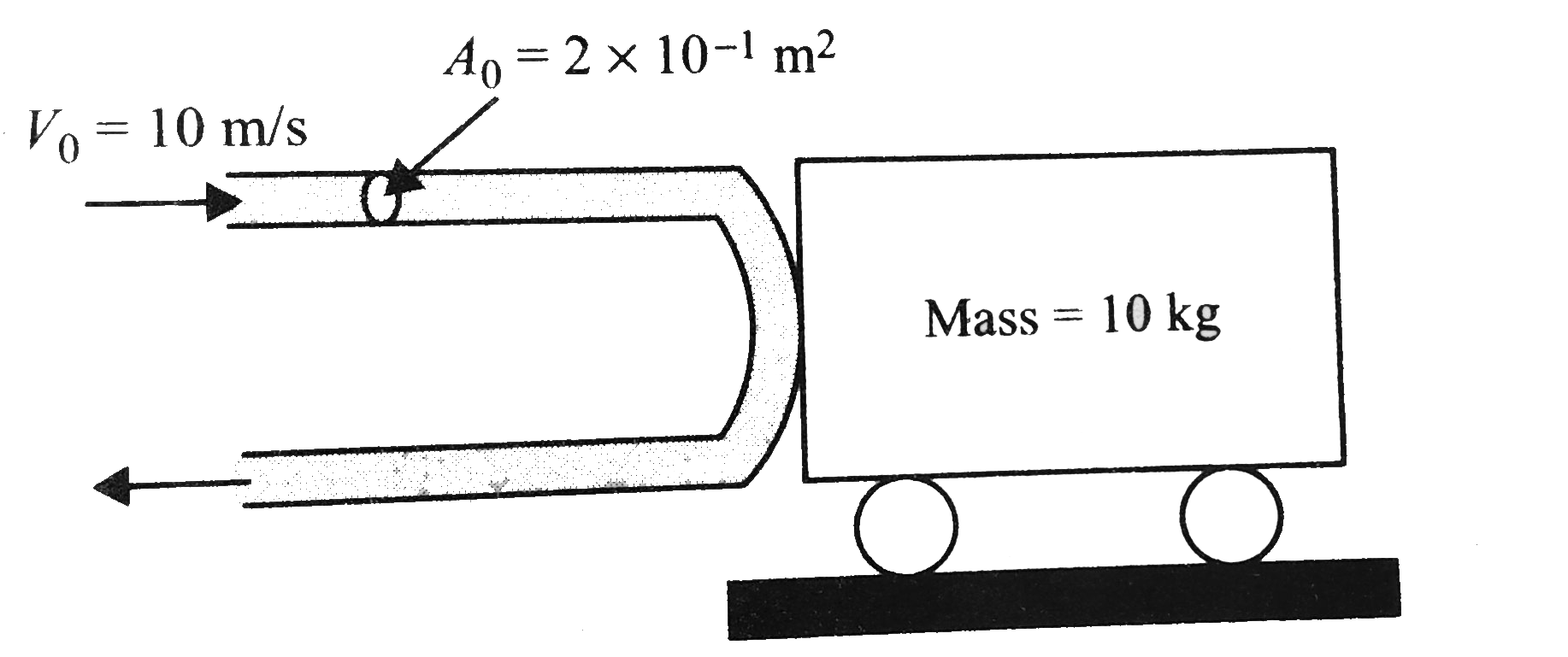
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
The time at which velocity of cart becomes 2ms is equal to
View SolutionTwo identical buggies move one after the other due to inertia (without friction) with the same velocity v0. A man of mass m rides the rear buggy. At a certain moment the man jumps into the front buggy with a velocity u relative to his buggy. Knowing that the mass of each buggy is equal to M, find the velocities with which the buggies will move after that.
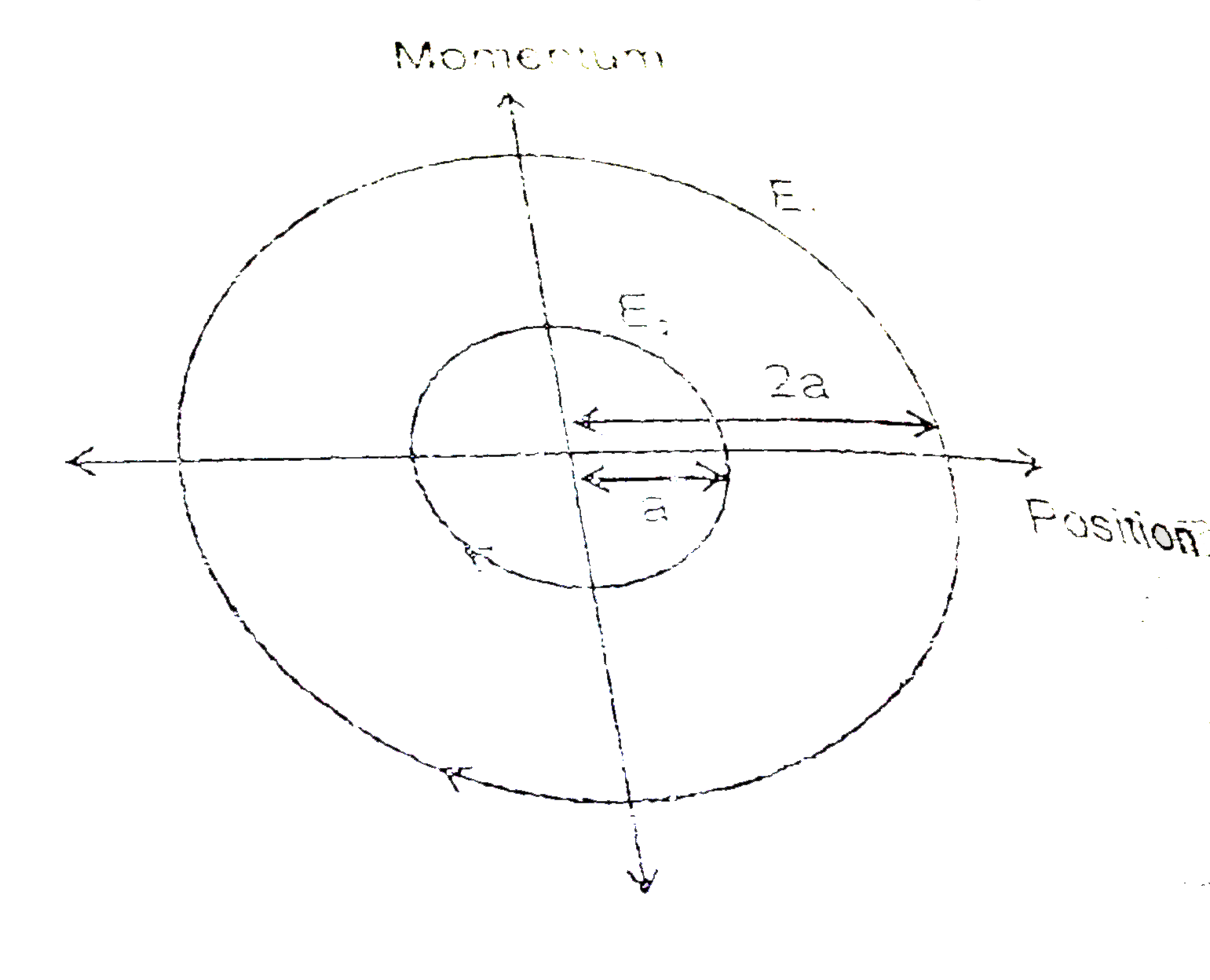
View SolutionPhase space diagrams are useful tools in analysing all kond of dynamical problems. Theya re especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical system in one-dimelnsion. for such systeam, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. for example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum. upwards (or to right) is positive and downwards (or to left) is negative.
The phase space diagram for simple harmonic motion is a circle cen-tered at the origin.In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 for E2 are the total mechanical energies respectively. Then
View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View SolutionConsider a situation where a cart carrying five boys is moving without friction due to inertia along a straight horizontal road, with a speed of 10 m/s. After travelling certain distance a boy jumps from the cart with a speed of 2 m/s with respect to cart in opposite direction to it. Then, second boy jumps with the same speed w.r.t. the cart, but in a perpendicular direction to the cart. The mass of the cart is 100 kg and mass of each boy is 20 kg.
Answer the following questions.
The speed of the cart after first boy has jumped out is
View Solution
