Two blocks of masses 5kg and 2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
4m/s,4m/s
10m/s,4m/s
4m/s,10m/s
10m/s,10m/s
The correct Answer is:C
To solve the problem, we need to find the magnitudes of the velocities of two blocks in the center of mass (CM) frame after the external kick is applied to the heavier block. Here’s a step-by-step solution:
Step 1: Identify the masses and initial conditions
- Mass of the heavier block (m1) = 5 kg
- Mass of the lighter block (m2) = 2 kg
- Initial velocity of the heavier block (V1) = 14 m/s (to the right)
- Initial velocity of the lighter block (V2) = 0 m/s (at rest)
Step 2: Calculate the velocity of the center of mass (V_cm)
The velocity of the center of mass for the system can be calculated using the formula:
Vcm=m1V1+m2V2m1+m2
Substituting the values:
Vcm=(5kg×14m/s)+(2kg×0m/s)5kg+2kg=70kg m/s7kg=10m/s
Step 3: Determine the velocities of the blocks in the center of mass frame
In the center of mass frame, the center of mass is at rest. Therefore, we need to subtract the velocity of the center of mass from the velocities of each block.
- For the heavier block (5 kg):
V1,CM=V1−Vcm=14m/s−10m/s=4m/s
- For the lighter block (2 kg):
V2,CM=V2−Vcm=0m/s−10m/s=−10m/s
(The negative sign indicates that the lighter block is moving in the opposite direction to the heavier block.)
Step 4: Find the magnitudes of the velocities
The magnitudes of the velocities are:
- Magnitude of velocity of the heavier block = |4 m/s| = 4 m/s
- Magnitude of velocity of the lighter block = |-10 m/s| = 10 m/s
Final Answer
The magnitudes of the velocities of the two blocks in the center of mass frame after the kick are:
- 4 m/s (for the 5 kg block)
- 10 m/s (for the 2 kg block)
Options
The correct option is: 4 m/s and 10 m/s.
---
- Mass of the heavier block (m1) = 5 kg
- Mass of the lighter block (m2) = 2 kg
- Initial velocity of the heavier block (V1) = 14 m/s (to the right)
- Initial velocity of the lighter block (V2) = 0 m/s (at rest)
The velocity of the center of mass for the system can be calculated using the formula:
Vcm=m1V1+m2V2m1+m2
Substituting the values:
Vcm=(5kg×14m/s)+(2kg×0m/s)5kg+2kg=70kg m/s7kg=10m/s
In the center of mass frame, the center of mass is at rest. Therefore, we need to subtract the velocity of the center of mass from the velocities of each block.
V1,CM=V1−Vcm=14m/s−10m/s=4m/s
V2,CM=V2−Vcm=0m/s−10m/s=−10m/s
(The negative sign indicates that the lighter block is moving in the opposite direction to the heavier block.)
The magnitudes of the velocities are:
- Magnitude of velocity of the heavier block = |4 m/s| = 4 m/s
- Magnitude of velocity of the lighter block = |-10 m/s| = 10 m/s
The magnitudes of the velocities of the two blocks in the center of mass frame after the kick are:
- 4 m/s (for the 5 kg block)
- 10 m/s (for the 2 kg block)
The correct option is: 4 m/s and 10 m/s.
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
Figure shows two blocks of masses 5kg and 2kg placed on a frictionless surface and connected with a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. Deduce (a) velocity gained by the centre of mass and (b) the separate velocities of the two blocks in the centre of mass coordinates just after the kick.

View SolutionTwo blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 4kg and 6kg are kept on a rough horizontal surface as shown. If the acceleration of 6kg block is 5n, then n is :

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionTwo blocks of masses 5 kg and 2 kg are kept in contact with each other on a frictionless horizontal surface. If a force of 14 N is applied on the larger block what is the acceleration of the system ? What is the contact force between the two blocks ?
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
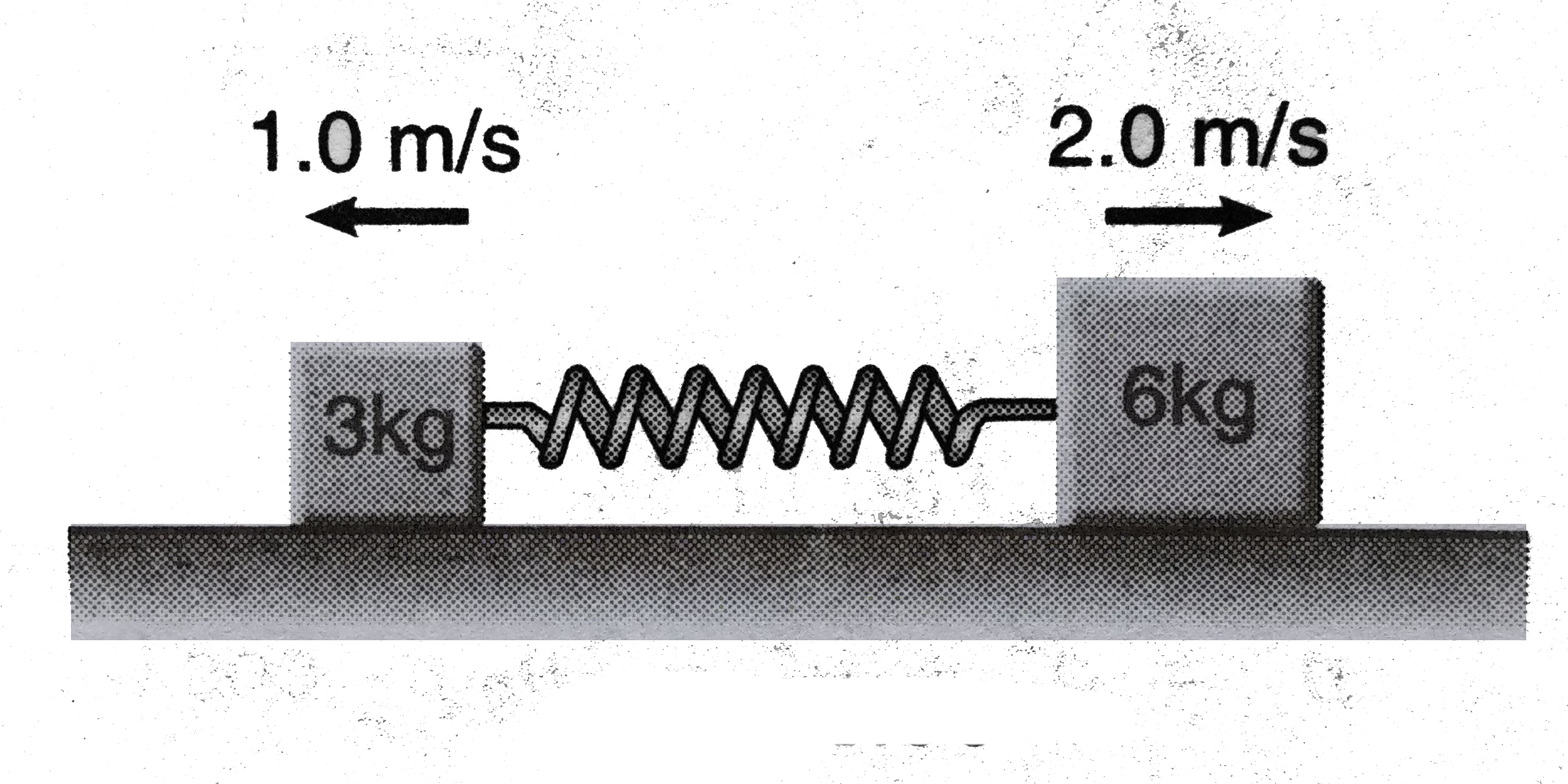
View Solution

