A projectile of mass 50kg is shot vertically upwards with an initial velocity of 100m/s. After 5s, it explodes into two fragments, one of which having a mass of 20kg travels vertically up with a velocity of 150m/s:
a. What is the velocity of the other fragment that instant?
b.Calculate the sum of rnornenta of fragment 3s after the explosion. What would have been the momentum of the projectile at this instant if there had been no explosion?
To solve the problem step by step, we will break it down into parts as outlined in the question.
Given Data:
- Mass of the projectile, m=50kg
- Initial velocity, u=100m/s
- Time before explosion, t=5s
- Mass of the first fragment, m1=20kg
- Velocity of the first fragment after explosion, v1=150m/s
Part (a): Finding the velocity of the second fragment just after the explosion.
1. Calculate the velocity of the projectile just before the explosion:
Using the equation of motion:
v=u+at
where a=−g=−10m/s2 (acceleration due to gravity acting downwards).
Substituting the values:
v=100m/s−10m/s2×5s=100−50=50m/s
2. Apply the conservation of momentum:
The total momentum before the explosion must equal the total momentum after the explosion.
Initial momentum=Final momentum
m⋅v=m1⋅v1+m2⋅v2
where m2=50kg−20kg=30kg and v2 is the velocity of the second fragment.
Substituting the known values:
50kg⋅50m/s=20kg⋅150m/s+30kg⋅v2
2500=3000+30v2
Rearranging gives:
30v2=2500−3000=−500
v2=−50030=−16.67m/s
Part (b): Calculate the sum of momenta of fragments 3 seconds after the explosion.
1. Calculate the velocity of the first fragment (20 kg) after 3 seconds:
Using the equation of motion again:
v′1=v1+a⋅t
where a=−10m/s2 and t=3s:
v′1=150m/s−10m/s2×3s=150−30=120m/s
2. Calculate the velocity of the second fragment (30 kg) after 3 seconds:
v′2=v2+a⋅t
v′2=−16.67m/s−10m/s2×3s=−16.67−30=−46.67m/s
3. Calculate the momentum of each fragment:
- Momentum of the first fragment:
p1=m1⋅v′1=20kg⋅120m/s=2400kg m/s
- Momentum of the second fragment:
p2=m2⋅v′2=30kg⋅(−46.67m/s)=−1400kg m/s
4. Total momentum after 3 seconds:
ptotal=p1+p2=2400kg m/s−1400kg m/s=1000kg m/s
5. Calculate the momentum of the projectile if there had been no explosion:
pno explosion=m⋅v=50kg⋅50m/s=2500kg m/s
Final Answers:
- a. The velocity of the other fragment just after the explosion is −16.67m/s.
- b. The sum of the momenta of the fragments 3 seconds after the explosion is 1000kg m/s, and the momentum of the projectile at that instant if there had been no explosion would have been 2500kg m/s.
- Mass of the projectile, m=50kg
- Initial velocity, u=100m/s
- Time before explosion, t=5s
- Mass of the first fragment, m1=20kg
- Velocity of the first fragment after explosion, v1=150m/s
Using the equation of motion:
v=u+at
where a=−g=−10m/s2 (acceleration due to gravity acting downwards).
v=100m/s−10m/s2×5s=100−50=50m/s
The total momentum before the explosion must equal the total momentum after the explosion.
Initial momentum=Final momentum
m⋅v=m1⋅v1+m2⋅v2
where m2=50kg−20kg=30kg and v2 is the velocity of the second fragment.
50kg⋅50m/s=20kg⋅150m/s+30kg⋅v2
2500=3000+30v2
Rearranging gives:
30v2=2500−3000=−500
v2=−50030=−16.67m/s
Using the equation of motion again:
v′1=v1+a⋅t
where a=−10m/s2 and t=3s:
v′1=150m/s−10m/s2×3s=150−30=120m/s
v′2=v2+a⋅t
v′2=−16.67m/s−10m/s2×3s=−16.67−30=−46.67m/s
- Momentum of the first fragment:
p1=m1⋅v′1=20kg⋅120m/s=2400kg m/s
- Momentum of the second fragment:
p2=m2⋅v′2=30kg⋅(−46.67m/s)=−1400kg m/s
ptotal=p1+p2=2400kg m/s−1400kg m/s=1000kg m/s
pno explosion=m⋅v=50kg⋅50m/s=2500kg m/s
- a. The velocity of the other fragment just after the explosion is −16.67m/s.
- b. The sum of the momenta of the fragments 3 seconds after the explosion is 1000kg m/s, and the momentum of the projectile at that instant if there had been no explosion would have been 2500kg m/s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A pebble thrown vertically upwards with an initial velocity 50 m s−1 comes to a stop in 5 s. Find the retardation.
View SolutionA mass of 1 kg is thrown up with a velocity of 100 m/s. After 5 seconds. It explodes into two parts. One parts of mass 400 g comes down with a velocity 25 m/s Calaculate the velocity of other parts:
View SolutionA mass of 1 kg is thrown up with a velocity of 100 m/s. After 5 seconds. It explodes into two parts. One parts of mass 400 g comes down with a velocity 25 m/s Calaculate the velocity of other parts:
View SolutionA ball of mass 0.20 kg is thrown vertically upwards with an initial velocity of 20 m s−1 .Calculate the maximum potential energy it gains as it goes up.
View SolutionAn object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use g=10m/s2.
View SolutionAt a given instant. A is moving with velocity of 5m/s upward. What is velocity of B at that time:
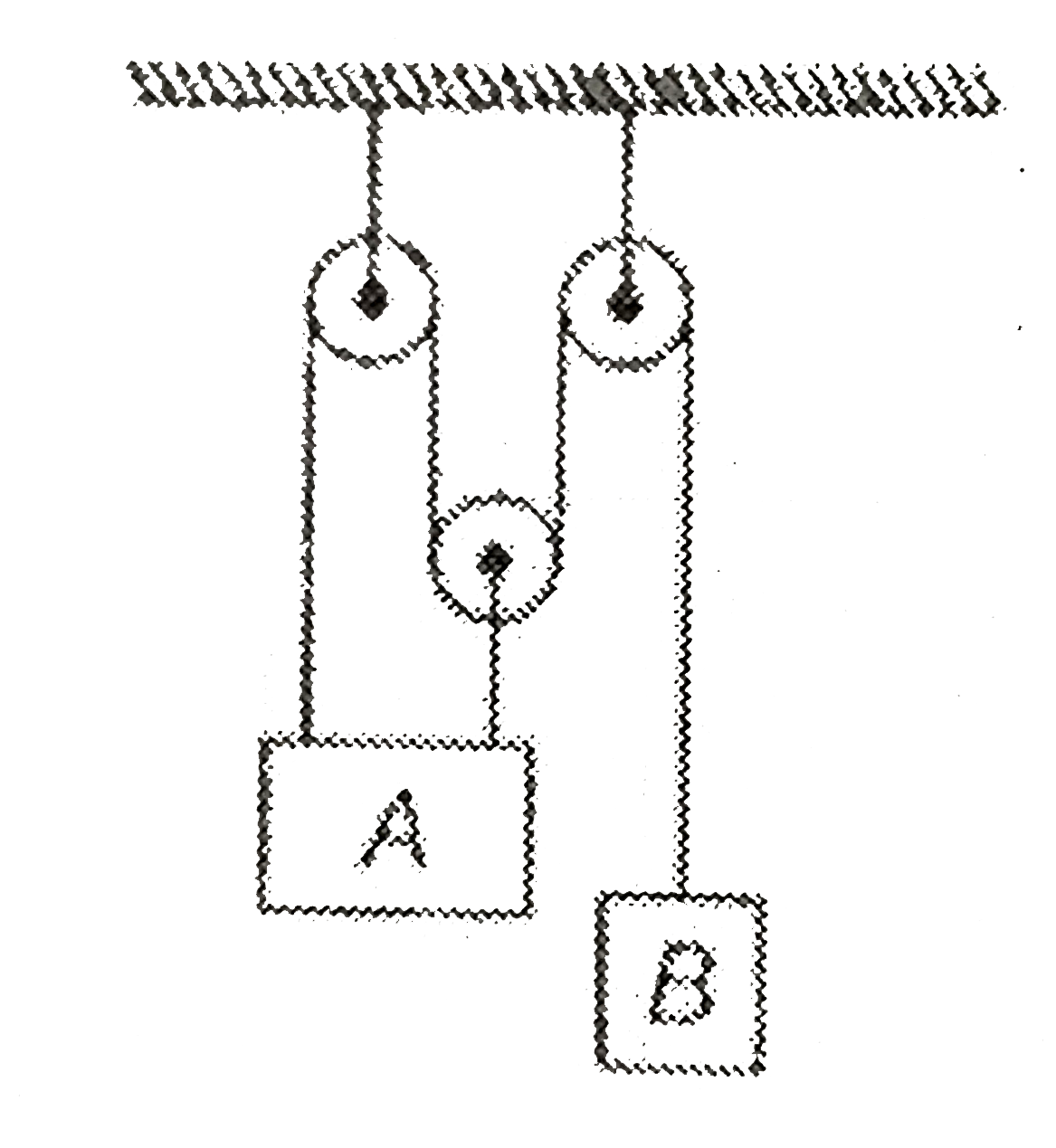
View SolutionA particle of mass 1 kg is thrown vertically upward with speed 100 m/s. After 5 sec it explodes into two parts. One part of mass 400 g comes back with speed 25 m/s, what is-the speed of the other part just after explosion? (g=10m/s2)
View SolutionA projectile moving vertically upwards with a velocity of 200 m/s breaks into two equal parts at the height of 490 m.one part starts moving vertically upwards with a velocity of 400 m/s.How much time after the break up wil the other part hit the ground?
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View Solution
