A pebble thrown vertically upwards with an initial velocity 50 m s−1 comes to a stop in 5 s. Find the retardation.
To solve the problem of finding the retardation of a pebble thrown vertically upwards, we can follow these steps:
1. Identify Given Values:
- Initial velocity (u) = 50 m/s (upwards)
- Final velocity (v) = 0 m/s (at the highest point, the pebble stops)
- Time (t) = 5 s
2. Use the First Equation of Motion:
The first equation of motion relates initial velocity, final velocity, acceleration, and time:
v=u+at
Here, we need to find the acceleration (a).
3. Substitute the Known Values:
Plugging in the known values into the equation:
0=50+a⋅5
4. Rearranging the Equation:
Rearranging the equation to solve for acceleration (a):
a⋅5=−50
a=−505
a=−10m/s2
5. Interpret the Result:
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity (which is expected when the pebble is thrown upwards). This means it is a retardation.
6. State the Retardation:
Since retardation is defined as the magnitude of negative acceleration, we can state:
Retardation=10m/s2
Final Answer:
The retardation of the pebble is 10 m/s².
---
- Initial velocity (u) = 50 m/s (upwards)
- Final velocity (v) = 0 m/s (at the highest point, the pebble stops)
- Time (t) = 5 s
The first equation of motion relates initial velocity, final velocity, acceleration, and time:
v=u+at
Here, we need to find the acceleration (a).
Plugging in the known values into the equation:
0=50+a⋅5
Rearranging the equation to solve for acceleration (a):
a⋅5=−50
a=−505
a=−10m/s2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity (which is expected when the pebble is thrown upwards). This means it is a retardation.
Since retardation is defined as the magnitude of negative acceleration, we can state:
Retardation=10m/s2
The retardation of the pebble is 10 m/s².
Topper's Solved these Questions
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (A)
Explore 28 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (A) ( Multiple choice type: )
Explore 5 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
Explore 1 Video
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise -4(B)Numericals
Explore 5 Videos
Similar Questions
A pobble is thrown vertically upwards from a bridge with an initial velocity of 4.9ms−1 . It strikes the water after 2 s. If acceleration due to gravity does the pebble strike the water ?
View SolutionA ball is thrown vertically upwards with an initial velocity of 49 m s−1. Calculate the time taken by it before it reaches the groung again (Take g= 9.8 m s−2)
View SolutionA toy car initially moving with uniform velocity of 18km h−1 comes to a stop in 2 s. Find the retardation of the car in S.I. units.
View SolutionA ball thrown vertically upwards with an initial velocity of 1.4m/s. The total displcement of the ball is
View SolutionA ball is thrown vertically upwards with an initial velocity of 5m/sec from point P as shown Q is a point 10m vertically below the point P. Then the speed of ball at point Q will be : (take g=10m/s2 and neglect air resistance)
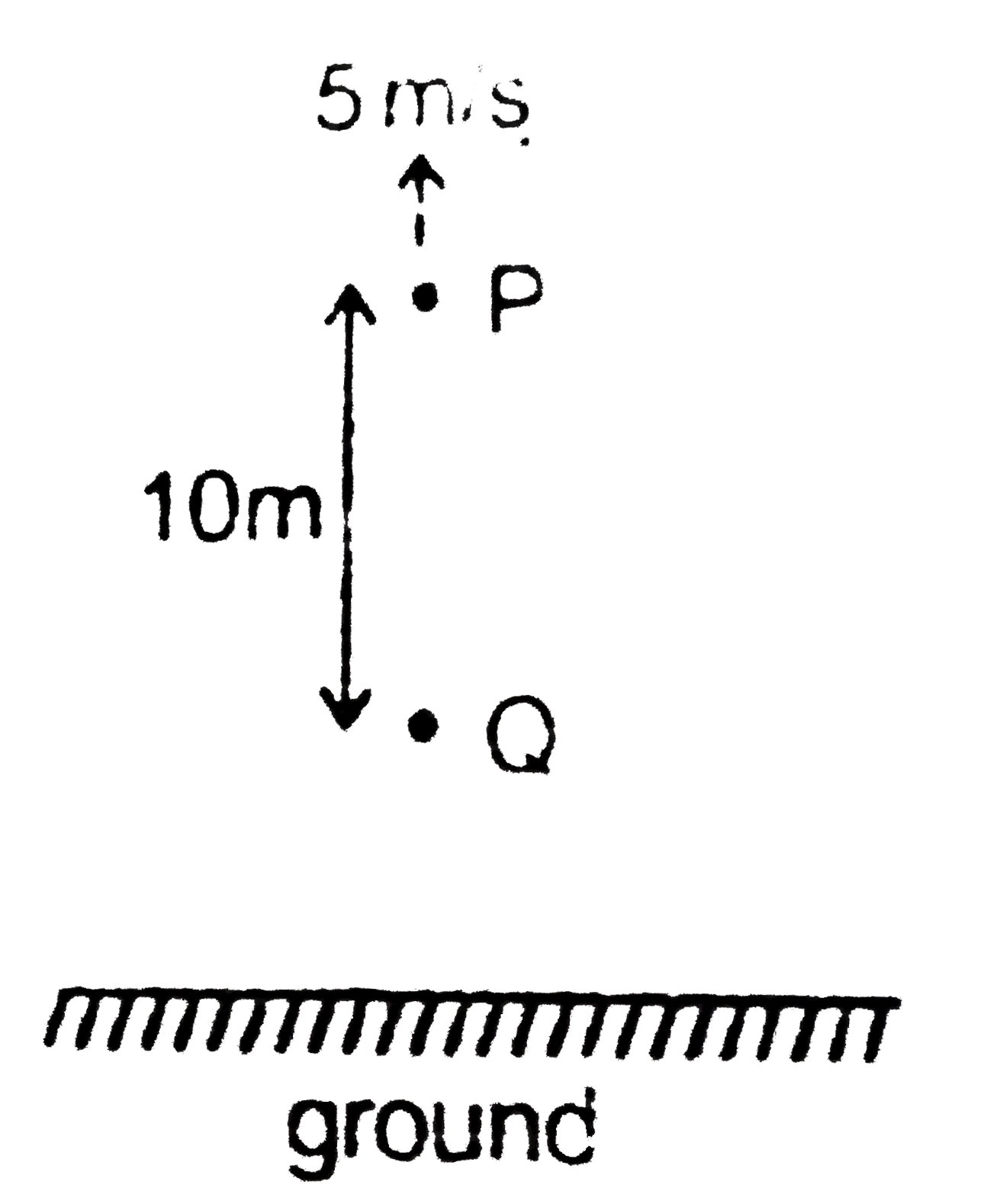
View SolutionA pebble is thrown vertically upwards from a bridge with an initial velocity of 4.9 m/s. It strikes the water after 2s. If acceleration due to gravity is 9.8m/s2(a) what is the height of the bridge? (b) with what velocity does that pebble strike the water?
View SolutionA body is thrown vertically upwards with an initial velocity of 9.8ms−1. What is its speed and direction after 1 s (g=9.8 m/s2). Also, find the height to which it will rise.
View SolutionA ball of mass 0.20 kg is thrown vertically upwards with an initial velocity of 20 m s−1 .Calculate the maximum potential energy it gains as it goes up.
View SolutionA stone is thrown vertically upwards with an initial velocity of 40 m s−1. Taking g = 10 m s−2, draw the velocity-time graph of the motion of stone till it comes back on the ground.
(i) Use graph to find the maximum height reached by the stone. (ii) What is the net displacement and total distance covered by the stone ?
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
 .
.
View Solution