The directioin of projection of particle is shown in the figure for an observer on trolley. An observer on the grond sees the ball rising vertically. The maximum height reached by the ball as seen from the troelley is

The correct Answer is:9
vx=vcos60∘=2√15ms−1
∴V=4√15ms−1
∴Vy=vsin60∘=4√15√32=2√45ms−1
Hmax=v2y2g=4×4520=9m.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A ball thrown by one player reaches the other in 2s. The maximum height attained by the ball above the point of projection will be about.
View SolutionA ball thrown by one player reaches the other in 2s. The maximum height attained by the ball above the point of projection will be about.
View SolutionA ball thrown by one player reaches the other in 2s. The maximum height attained by the ball above the point of projection will be about.
View SolutionA boy throws n balls per second at regular time intervals. When the first ball reaches the maximum height he throws the second one vertically up. The maximum height reached by each ball is
View SolutionA boy throws n balls per second at regular time intervals.When the first ball reaches the maximum height he throws the second one vertically up .The maximum height reached by each ball is
View SolutionA ball is projected vertically up such that it passes thorugh a fixed point after a time t1 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .
.
View Solution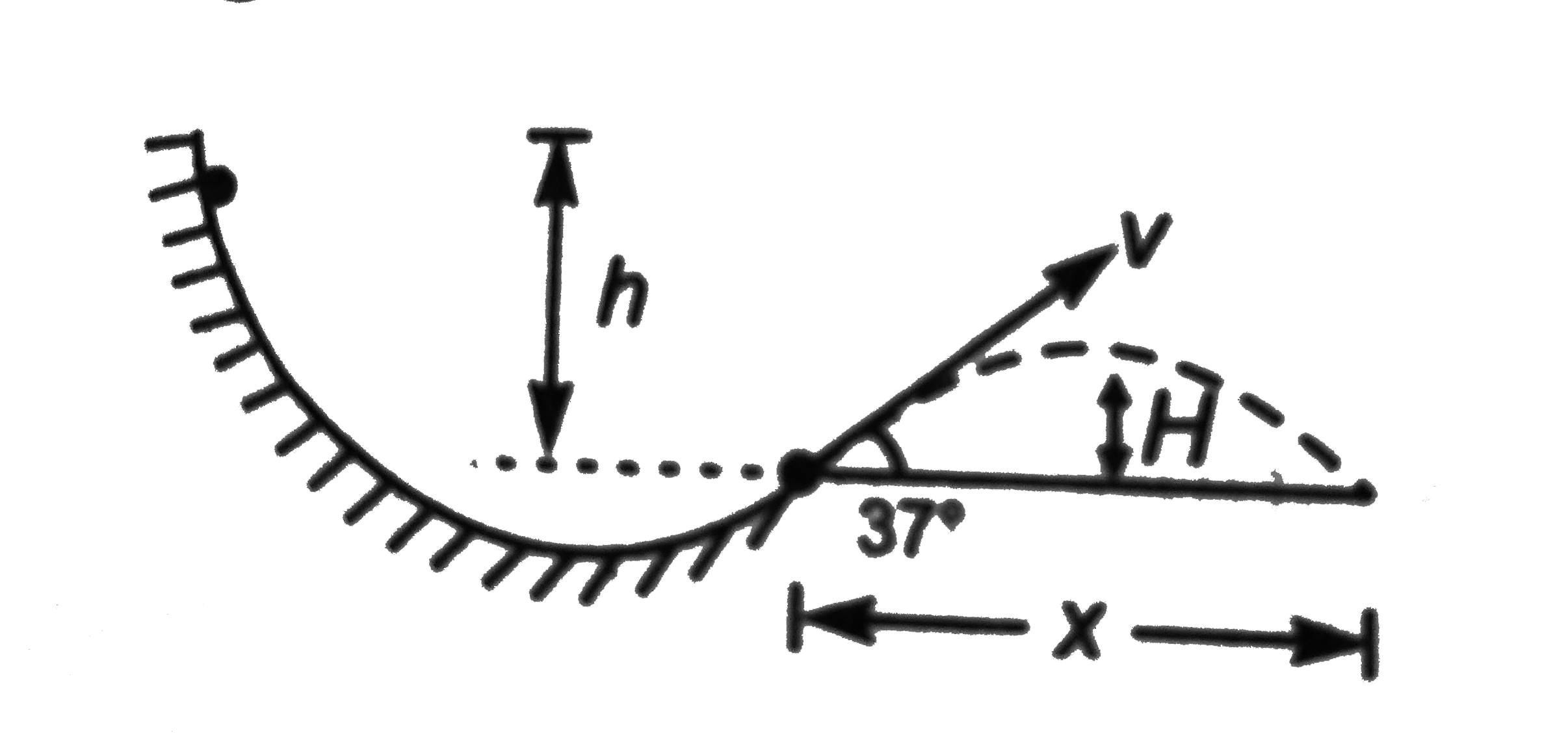
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
View SolutionA ball is thrown from the top of a tower in vertically upward direction. Velocity at a point h m below the point of projection is twice of the velocity at a point h m above the point of projection. Find the maximum height reached by the ball above the top of tower.
View SolutionA ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

Let h be the maximum height from ground reached by ball after leaving track at B. Then,
View SolutionTwo particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
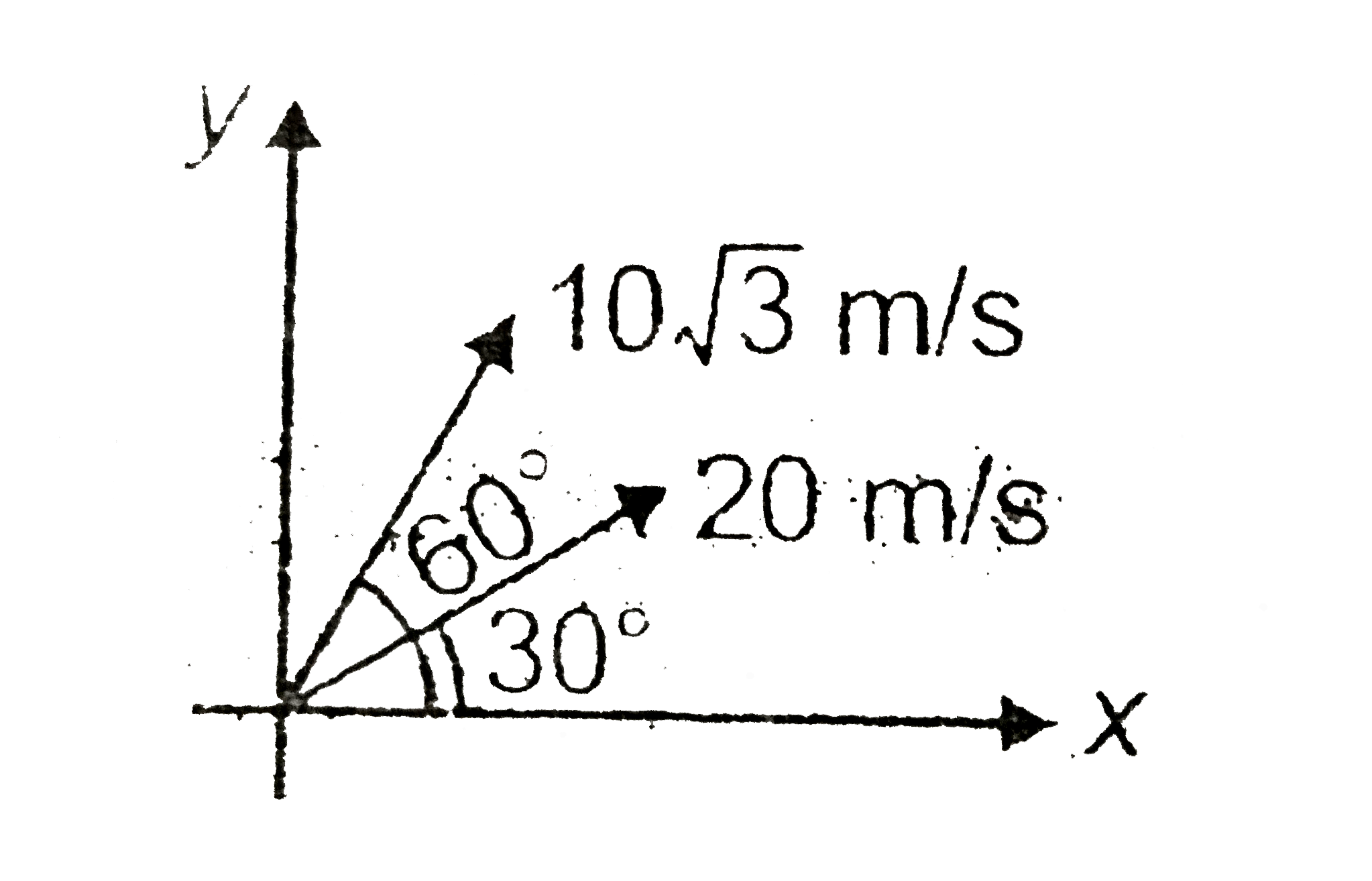
View Solution
