A boy throws n balls per second at regular time intervals.When the first ball reaches the maximum height he throws the second one vertically up .The maximum height reached by each ball is
A) g2(n−1)2
B) g2n2
C) gn2
D) gn
The correct Answer is:B
To solve the problem, we will go through the following steps:
Step 1: Understand the Time Interval Between Throws
The boy throws n balls per second at regular time intervals. Therefore, the time interval t between two successive throws is given by:
t=1n
Hint: Remember that if n balls are thrown in one second, the time between each throw is the reciprocal of n.
Step 2: Determine the Time to Reach Maximum Height
When the first ball is thrown, it takes a certain amount of time to reach its maximum height. This time is equal to the time interval t since the second ball is thrown when the first ball reaches its maximum height. Thus, the time taken t to reach maximum height is:
t=1n
Hint: The time to reach maximum height is the same as the time interval between throws.
Step 3: Use Kinematic Equations to Find Initial Velocity
At the maximum height, the final velocity v of the ball is 0. We can use the kinematic equation:
v=u−gt
Where:
- v = final velocity (0 at maximum height)
- u = initial velocity (velocity of projection)
- g = acceleration due to gravity
- t = time taken to reach maximum height
Substituting v=0 and t=1n:
0=u−g(1n)
Rearranging gives:
u=g(1n)=gn
Hint: Use the fact that the final velocity at the maximum height is zero to find the initial velocity.
Step 4: Calculate the Maximum Height
The maximum height h reached by the ball can be calculated using the formula:
h=u22g
Substituting the value of u:
h=(gn)22g
This simplifies to:
h=g2n2⋅2g=g2n2
Hint: Remember to square the initial velocity and divide by 2g to find the maximum height.
Step 5: Conclusion
Thus, the maximum height reached by each ball is:
h=g2n2
This matches with option (b) from the given choices.
Final Answer: The maximum height reached by each ball is g2n2.
The boy throws n balls per second at regular time intervals. Therefore, the time interval t between two successive throws is given by:
t=1n
When the first ball is thrown, it takes a certain amount of time to reach its maximum height. This time is equal to the time interval t since the second ball is thrown when the first ball reaches its maximum height. Thus, the time taken t to reach maximum height is:
t=1n
At the maximum height, the final velocity v of the ball is 0. We can use the kinematic equation:
v=u−gt
Where:
- v = final velocity (0 at maximum height)
- u = initial velocity (velocity of projection)
- g = acceleration due to gravity
- t = time taken to reach maximum height
0=u−g(1n)
Rearranging gives:
u=g(1n)=gn
The maximum height h reached by the ball can be calculated using the formula:
h=u22g
Substituting the value of u:
h=(gn)22g
This simplifies to:
h=g2n2⋅2g=g2n2
Thus, the maximum height reached by each ball is:
h=g2n2
This matches with option (b) from the given choices.
Similar Questions
A body is thrown vertically up reaches a maximum height of 78.4 m. After what time it will reach the ground from the maximum height reached ?
View SolutionA boy throws a ball in air in such a manner that when the ball is at its maximum height he throws another ball. If the balls are thrown with the time difference 1 second, the maximum height attained by each ball is
View Solution
Knowledge Check
- Question 1 - Select One
In the question number 62. the maximum height attained by the ball is
A11.25 mB48.2 mC23. 5 mD68 m
The directioin of projection of particle is shown in the figure for an observer on trolley. An observer on the grond sees the ball rising vertically. The maximum height reached by the ball as seen from the troelley is
 View Solution
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
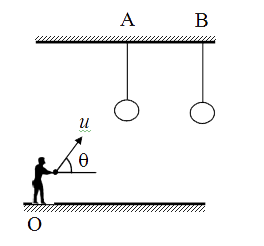
The maximum height attained by the ball above the floor is:View SolutionA ball is projected vertically up such that it passes thorugh a fixed point after a time t1 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .View Solution
.View SolutionA man is standing on top of a building 100 m high. He throws two ball vertically, one at t=0 and after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. At t=2, both the balls reach to their maximum heights at this time the vertical gap between first and second ball is +15m.
Q. The speed of first ball isView SolutionA cricket player throws the ball to have the maximum horizontal range of 120m. If the throws the ball vertically with same velocity what is the maximum height it can reach ?
View SolutionA person can throw a ball vertically upto maximum height of 20 mt. How far can he throw the ball.
View SolutionA lift is moving up with acceleration a A person inside the ligt throws the ball upwards with a velocity u relativeto hand.
a. What is the time of flight of the ball?
b. What is the maximum height reached by the ball in the lift?
 View Solution
View Solution
