A particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
The correct Answer is:2π,πr
To solve the problem, we need to determine the displacement and distance covered by a particle moving in a circle of radius R after completing half of its period of revolution.
1. Understanding the Motion:
- The particle is moving in a circular path with a radius R.
- Half of the period of revolution means the particle has moved from one point on the circle to the point directly opposite it.
2. Calculating the Distance Covered:
- The distance covered by the particle in half a revolution is half the circumference of the circle.
- The circumference C of a circle is given by the formula:
C=2πR
- Therefore, the distance covered in half the revolution is:
Distance=C2=2πR2=πR
3. Calculating the Displacement:
- Displacement is defined as the shortest distance between the initial and final positions of the particle.
- When the particle moves half the circle, its initial position and final position are at opposite ends of the diameter.
- The displacement, which is the length of the diameter, is given by:
Displacement=2R
Final Answers:
- Displacement: 2R
- Distance Covered: πR
- The particle is moving in a circular path with a radius R.
- Half of the period of revolution means the particle has moved from one point on the circle to the point directly opposite it.
- The distance covered by the particle in half a revolution is half the circumference of the circle.
- The circumference C of a circle is given by the formula:
C=2πR
- Therefore, the distance covered in half the revolution is:
Distance=C2=2πR2=πR
- Displacement is defined as the shortest distance between the initial and final positions of the particle.
- When the particle moves half the circle, its initial position and final position are at opposite ends of the diameter.
- The displacement, which is the length of the diameter, is given by:
Displacement=2R
- Displacement: 2R
- Distance Covered: πR
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:True or False
Explore 2 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Integer Type
Explore 17 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
A particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
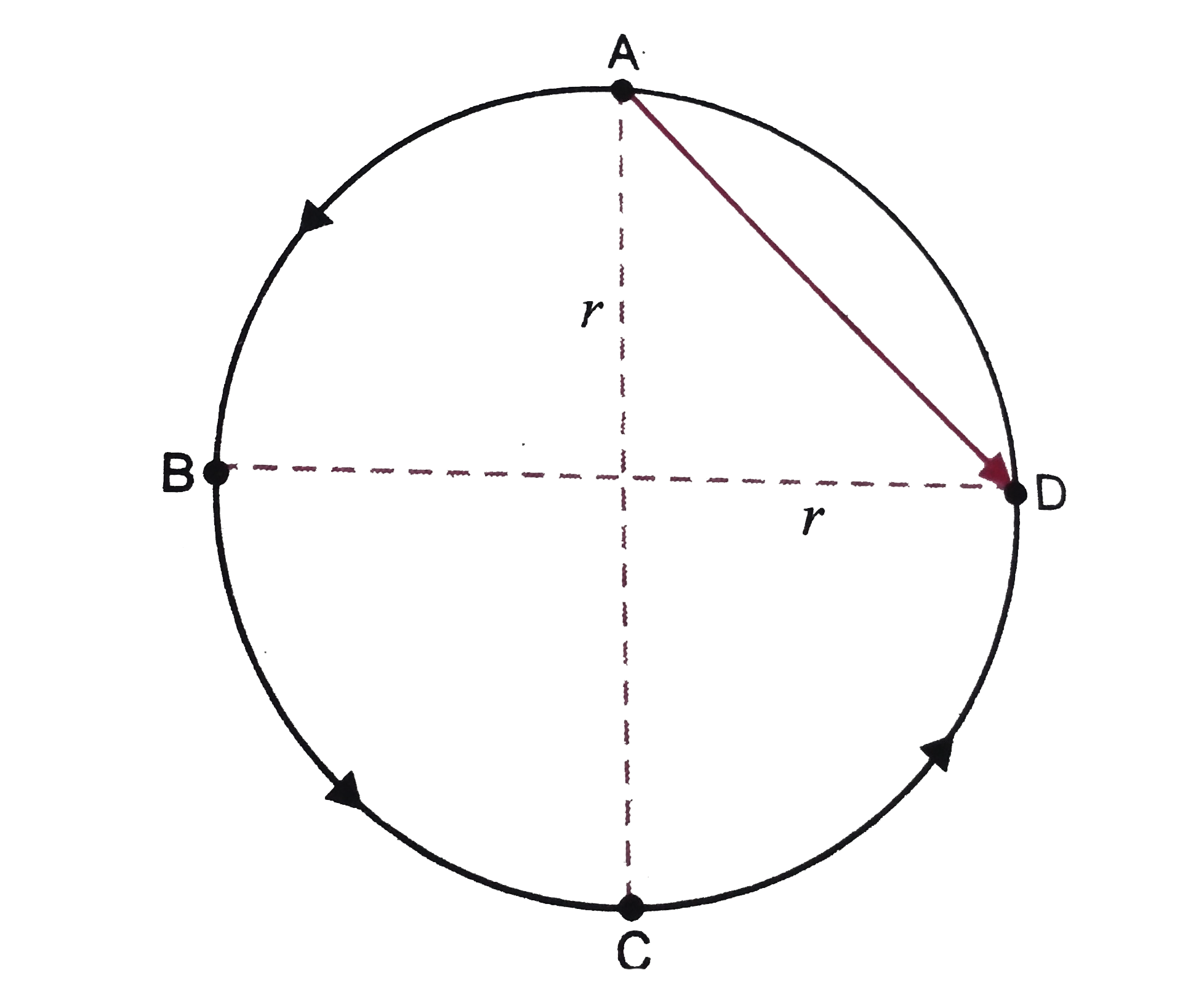
View SolutionA particle is moving in a circle of radius R.
a. What is its displacement when it covers (i) half the circle, (ii) full circle?
b. What is its distance when it comers (i) half the the circle and (ii) full circle ?.
 .
.
View SolutionA particle moves on a circular path of radius 'r'. It completes one revolution in 40s. Calculate distances displacement in 2 min 20 s.
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionThe radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. find the acceleration due to the gravitation of the plane at its surface.
View SolutionA particle moves along a circular path of radius R. The distance and displacement of a particle after one completer revolution is
View SolutionA particle move in a semicircular of radius R from O to A . Then it moves parallel to z-axis covering distance R upto B. Finally it moves along BC parallel to y-axis throuth a distance 2R. Find the ratio of D/s.
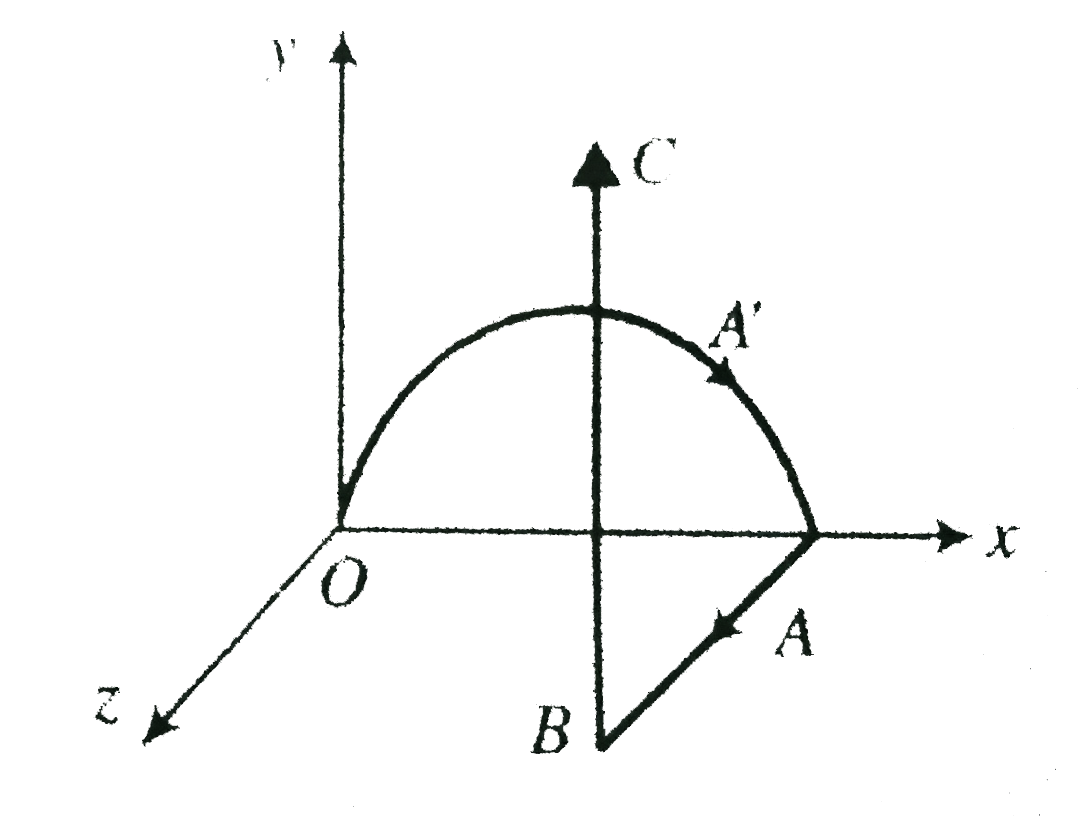 .
.
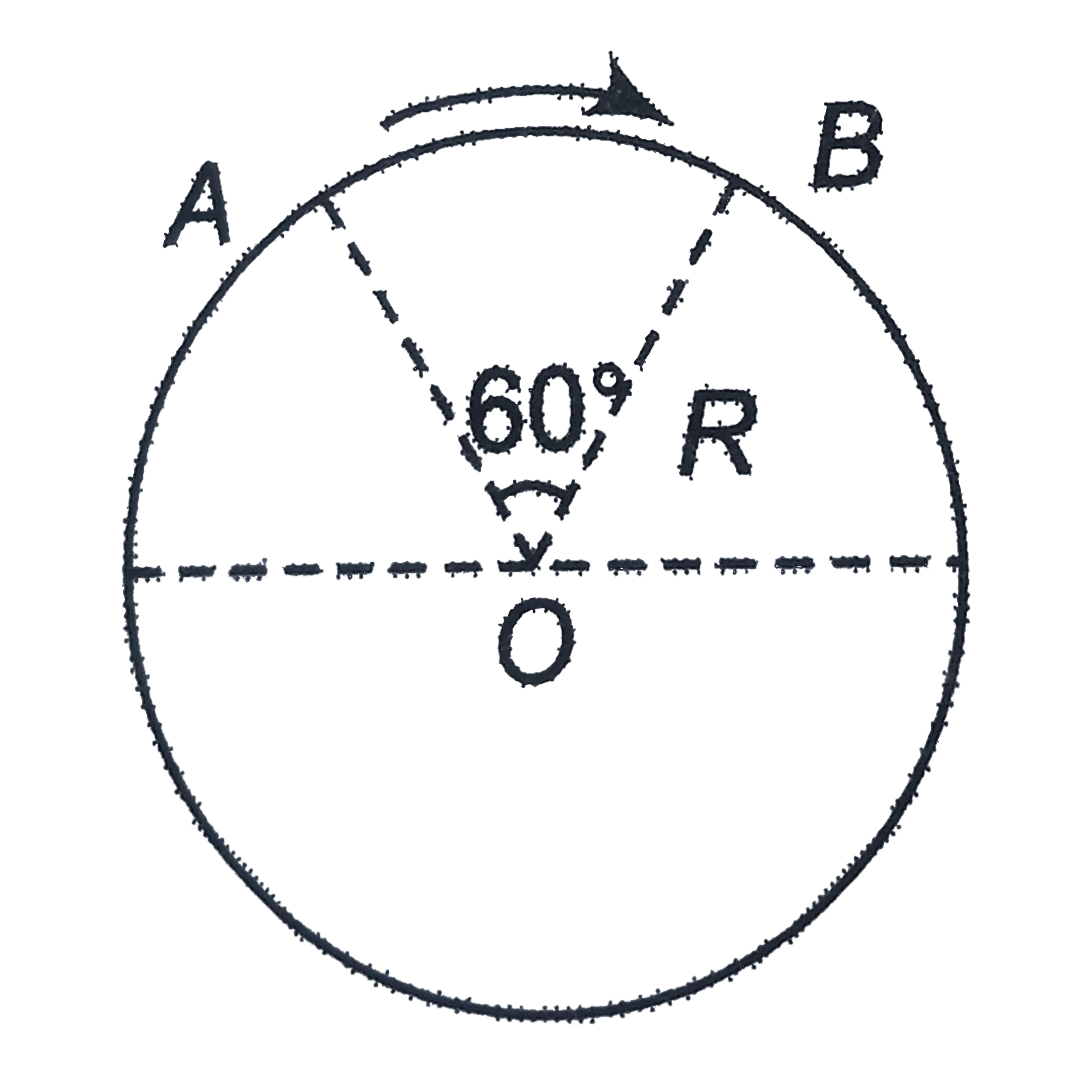
View SolutionA particle moves in a of radius R from A to B, as shown in the figure. Find the distance and displacement covered.
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionIf the displacement of a particle is zero, then distance covered by it
View Solution