A particle move in a semicircular of radius from to . Then it moves parallel to z-axis covering distance upto . Finally it moves along parallel to y-axis throuth a distance . Find the ratio of .
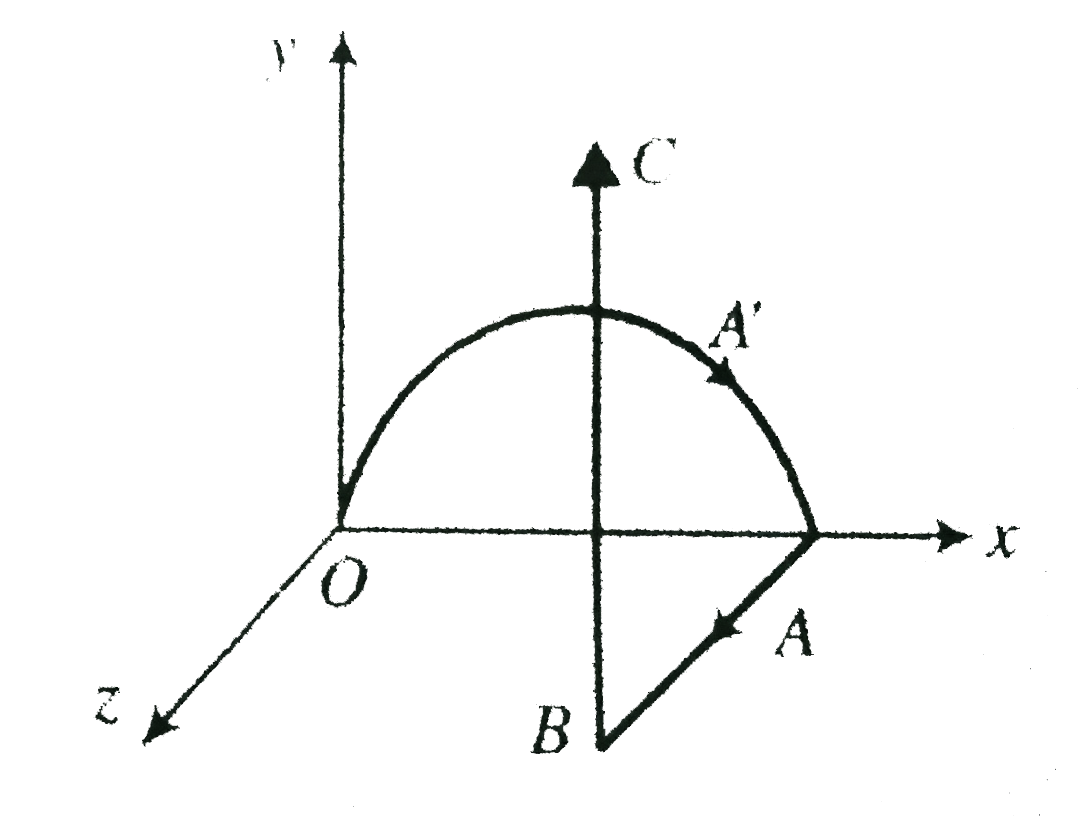 .
.
The distance , that is, length of the actual path covered by time the particle as shown in
 .
.
length of the semicircle length
length . This .
Since , and , the
coorkenates of can be given as . Then the position of is expresed as:
As , Substituting and ,
we obtains .
Its magnitude
Hence, .
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moves in a of radius R from A to B, as shown in the figure. Find the distance and displacement covered.
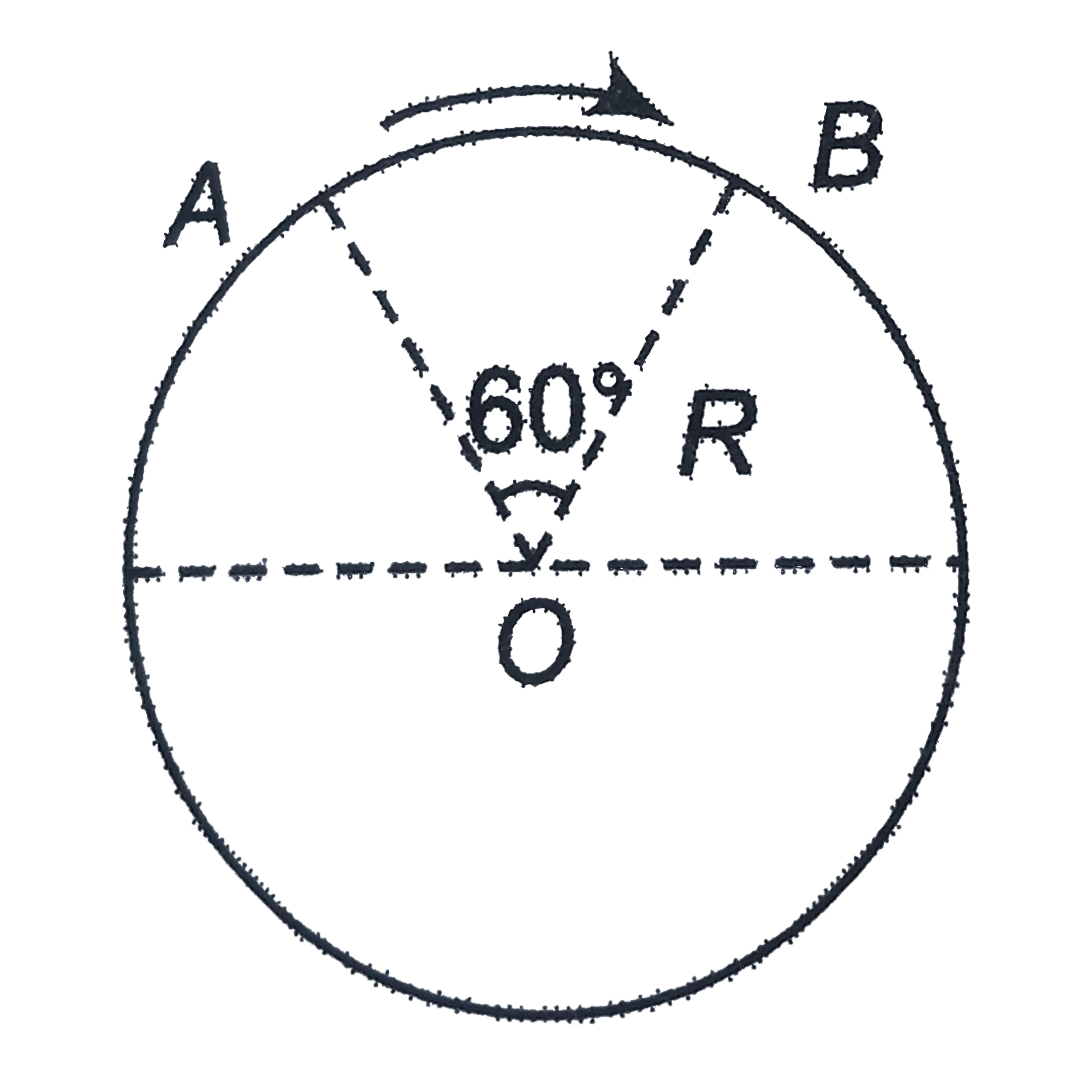
View SolutionA particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
View SolutionA particle moves on a circular path of radius 'r'. It completes one revolution in 40s. Calculate distances displacement in 2 min 20 s.
View SolutionA particle moves along a circular path of radius R. The distance and displacement of a particle after one completer revolution is
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is

View SolutionA particle moves with a speed v in a circle of radius R .when the particle reaches from A to B as shown in the figure, then Y component of average velocity is
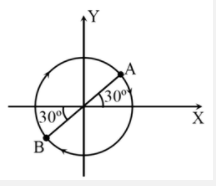
View SolutionThe moment of inertia of a circular loop of radius R, at a distance of R/2 around a rotating axis parallel to horizontal diameter of loop is
View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View SolutionA particle is moving along a circle of radius R with a uniform speed v. At t=0 , the particle is moving along the east. Find the average acceleration (magnitude and direction) in 1/4th revolution.
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is

View Solution
