Acceleration of particle moving rectilinearly is (where x is position in metre and a in ms^(-2))x 9in meter) will the particle again come to instantaneous rest?
The correct Answer is:4
To solve the problem, we need to find the position x where the particle comes to instantaneous rest again, given the acceleration function a=4−2x.
1. Understand the relationship between acceleration, velocity, and position:
The acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=vdvdx
Therefore, we can set up the equation:
vdvdx=4−2x
2. Separate variables:
Rearranging gives us:
vdv=(4−2x)dx
3. Integrate both sides:
We will integrate the left side with respect to v and the right side with respect to x:
∫vdv=∫(4−2x)dx
The left side integrates to:
v22
The right side integrates to:
4x−x2+C
where C is the constant of integration.
4. Combine the results:
Thus, we have:
v22=4x−x2+C
5. Determine the constant C:
We know that at x=0, the particle is at instantaneous rest, which means v=0. Substituting these values into the equation:
0=4(0)−(0)2+C⟹C=0
Therefore, the equation simplifies to:
v22=4x−x2
6. Find when the particle comes to rest again:
The particle comes to rest when v=0:
0=4x−x2
Rearranging gives:
x2−4x=0
Factoring out x:
x(x−4)=0
This gives us two solutions:
x=0orx=4
7. Conclusion:
The particle comes to instantaneous rest again at x=4 meters.
Final Answer:
The particle will again come to instantaneous rest at x=4 meters.
The acceleration a can be expressed in terms of velocity v and position x using the chain rule:
a=vdvdx
Therefore, we can set up the equation:
vdvdx=4−2x
Rearranging gives us:
vdv=(4−2x)dx
We will integrate the left side with respect to v and the right side with respect to x:
∫vdv=∫(4−2x)dx
The left side integrates to:
v22
The right side integrates to:
4x−x2+C
where C is the constant of integration.
Thus, we have:
v22=4x−x2+C
We know that at x=0, the particle is at instantaneous rest, which means v=0. Substituting these values into the equation:
0=4(0)−(0)2+C⟹C=0
Therefore, the equation simplifies to:
v22=4x−x2
The particle comes to rest when v=0:
0=4x−x2
Rearranging gives:
x2−4x=0
Factoring out x:
x(x−4)=0
This gives us two solutions:
x=0orx=4
The particle comes to instantaneous rest again at x=4 meters.
The particle will again come to instantaneous rest at x=4 meters.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Fill in the blanks
Explore 4 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:True or False
Explore 2 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Linked Comprehension Type
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Knowledge Check
The displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
Aa. 4 mBb. 8 mCc. 12 mDd. 16 m
A particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionA charged particle having charge q and mass m moves rectilinearly under the action of the electric field E(x)=(4−3x)N/C where x is the distance was initially at rest. The distance travelled by the particle till it comes instantaneously to rest again for the first time, is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
When is the object at rest?
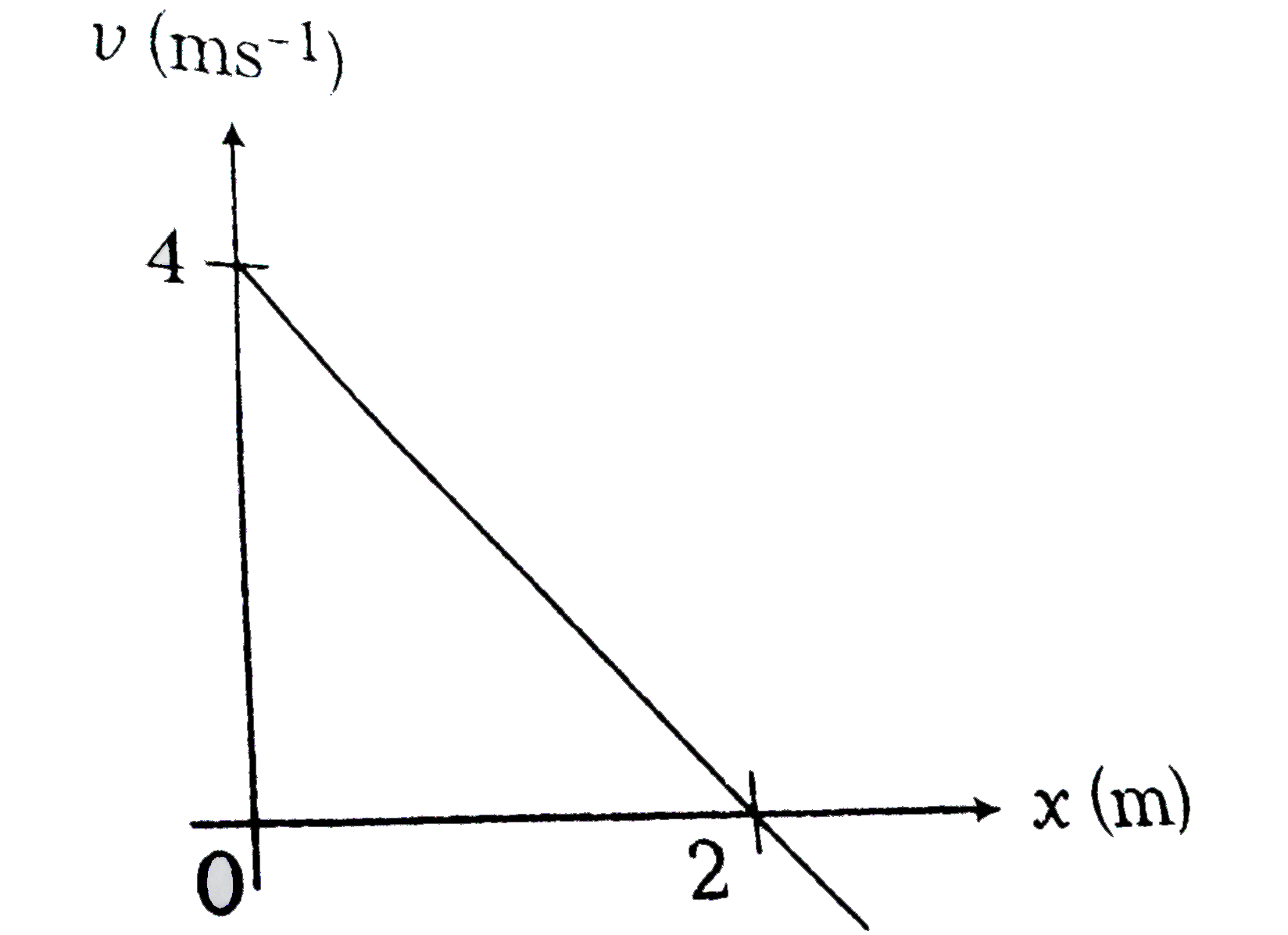
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
View SolutionThe acceleration of a particle moving along x-axis is a=−100x+50. It is released from x=2. Here a and x are in S.I units. The motion of particle will be:
View SolutionA particle of charge q and mass m is subjected to an electric field E=E0(1−ax2) in the x - direction, where a and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
View SolutionA particle moves in a straight line and its position x at time t is given by x2=2+t. Its acceleration is given by :-
View Solution