A force F=−kˆi+xˆj where k is a positive constant, acts on a praricle moving in the xy plane. Starting from the origin, the particle is taken along the positive x - axis to the point (a,0) and then parallel to the y-axis to the point (a,a) the total work done by the formce on the particle is
(a) −2Ka2
(b) 2Ka2
(c) −Ka2
(d) Ka2
The correct Answer is:D
w=∫fxdx+∫fydy=−k∫ydx−k∫xdy

From 0 to A, dy=0, y=0
So WOA=0
From A to B: dx=0, x=a
WAB=−ka∫a0dy=−ka2
Hence, total work done
WT=WOA+WAB=0−ka2−ka2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (assertion-reasoning)
1 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
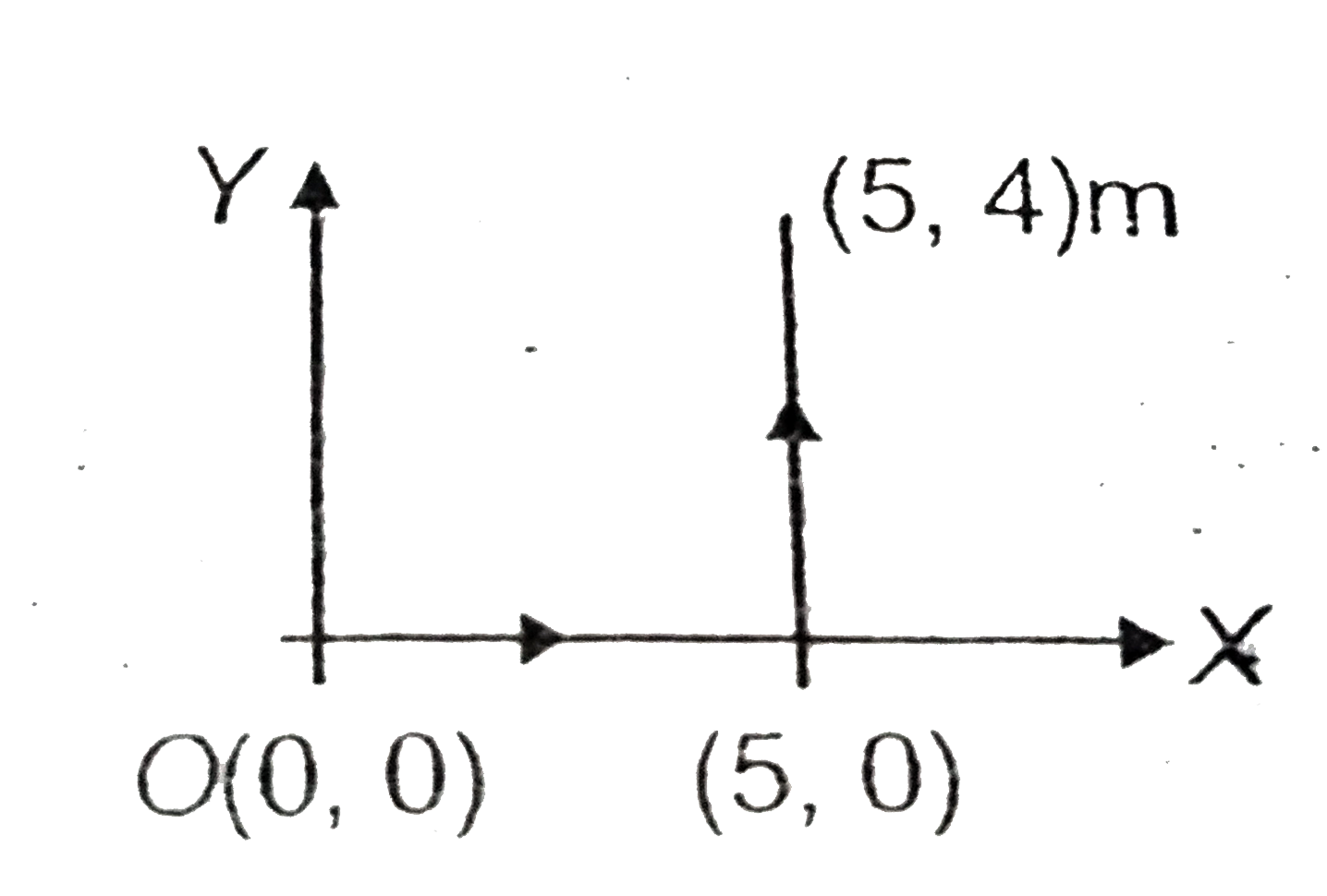
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA particle starts from the origin, goes along x-axis to the point (10 m, 0) and then returns along. The same line to the point (-10 m, 0). The distance and displacement of the particle during the trip are
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
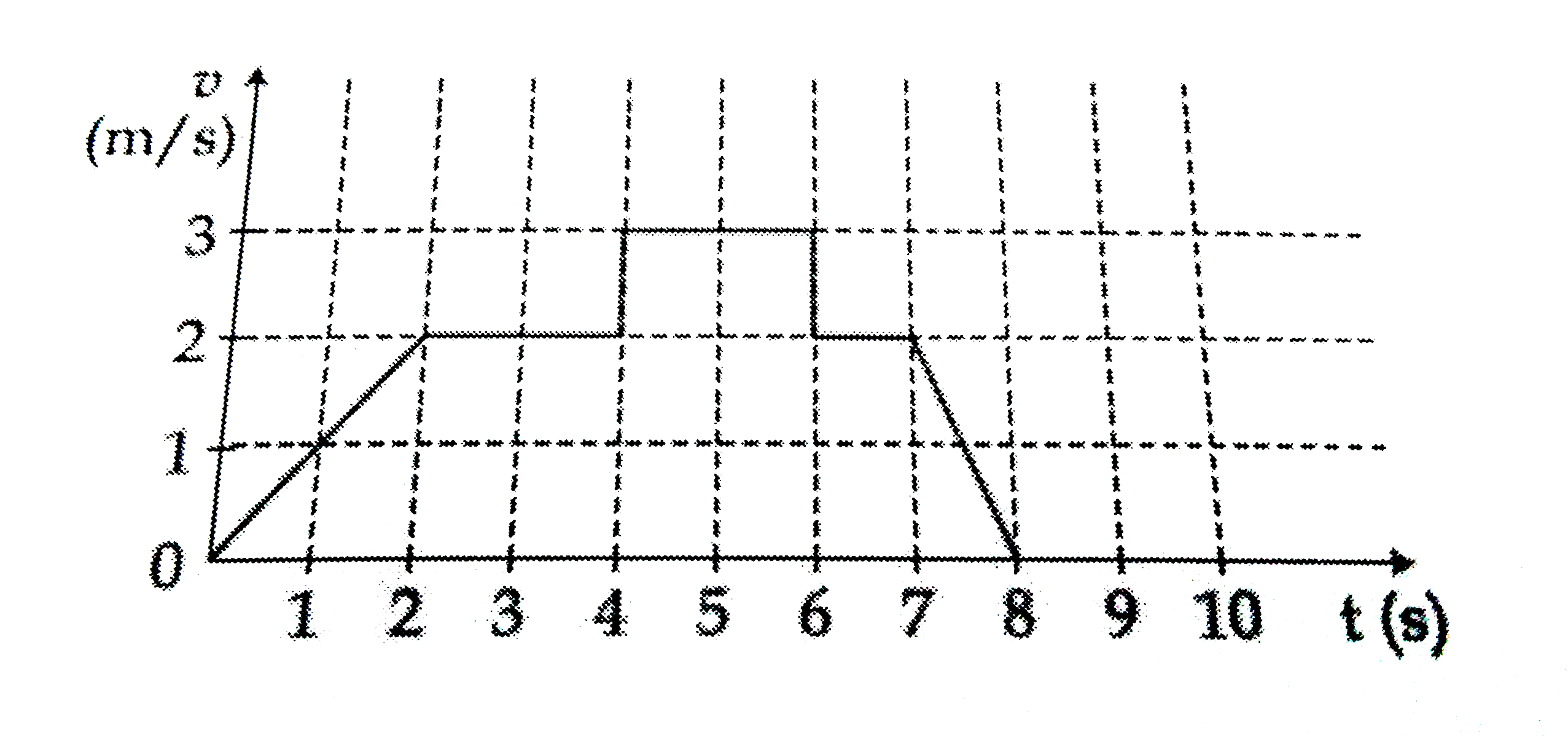
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
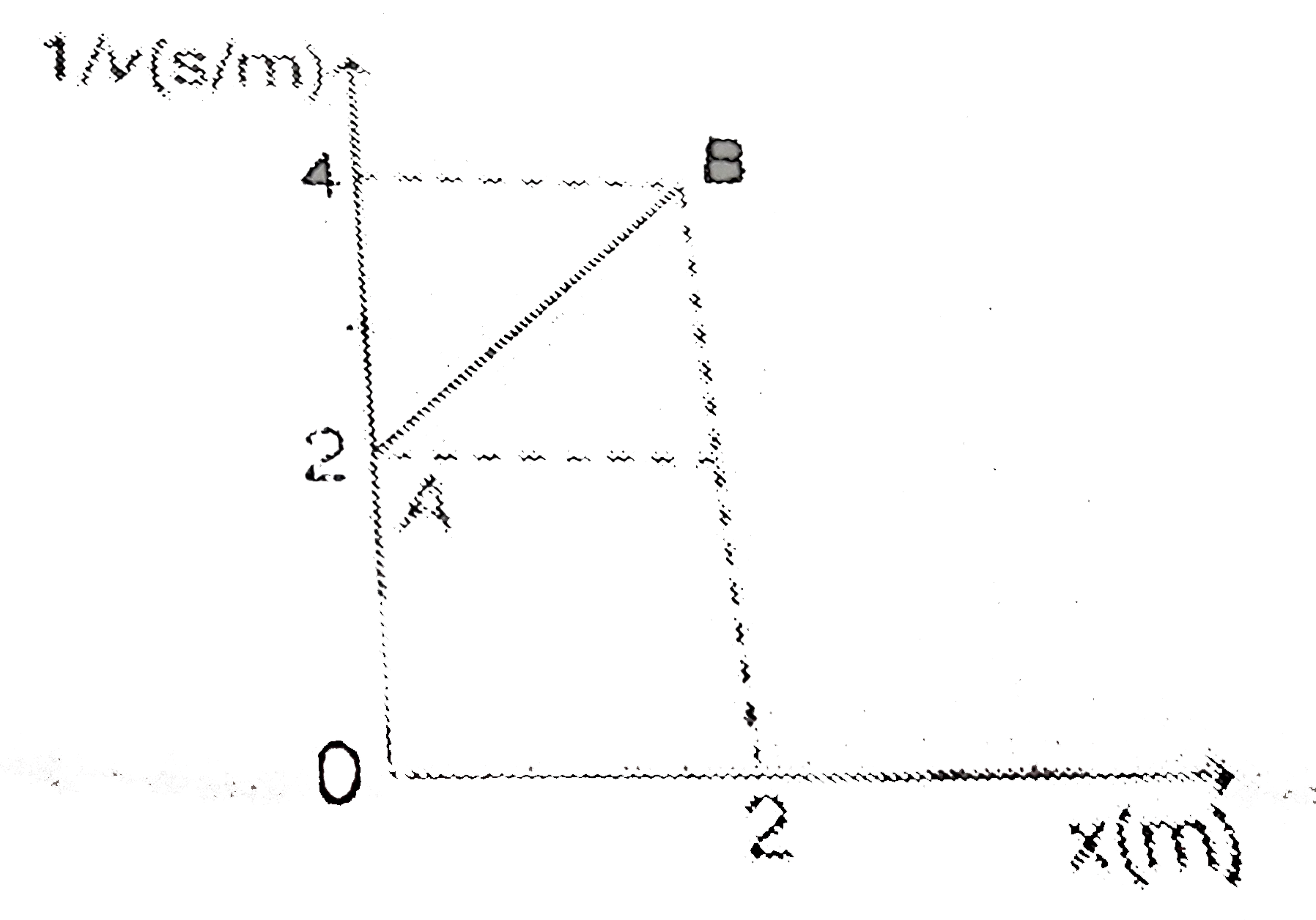
View SolutionThe 1/v versus positions graph of a particle is shown in the figure, where v is the velocity of the particle. The particle is moving in a straight line aloing positive x- axis.Find the time taken by the particle to reach from the point A to B in second.
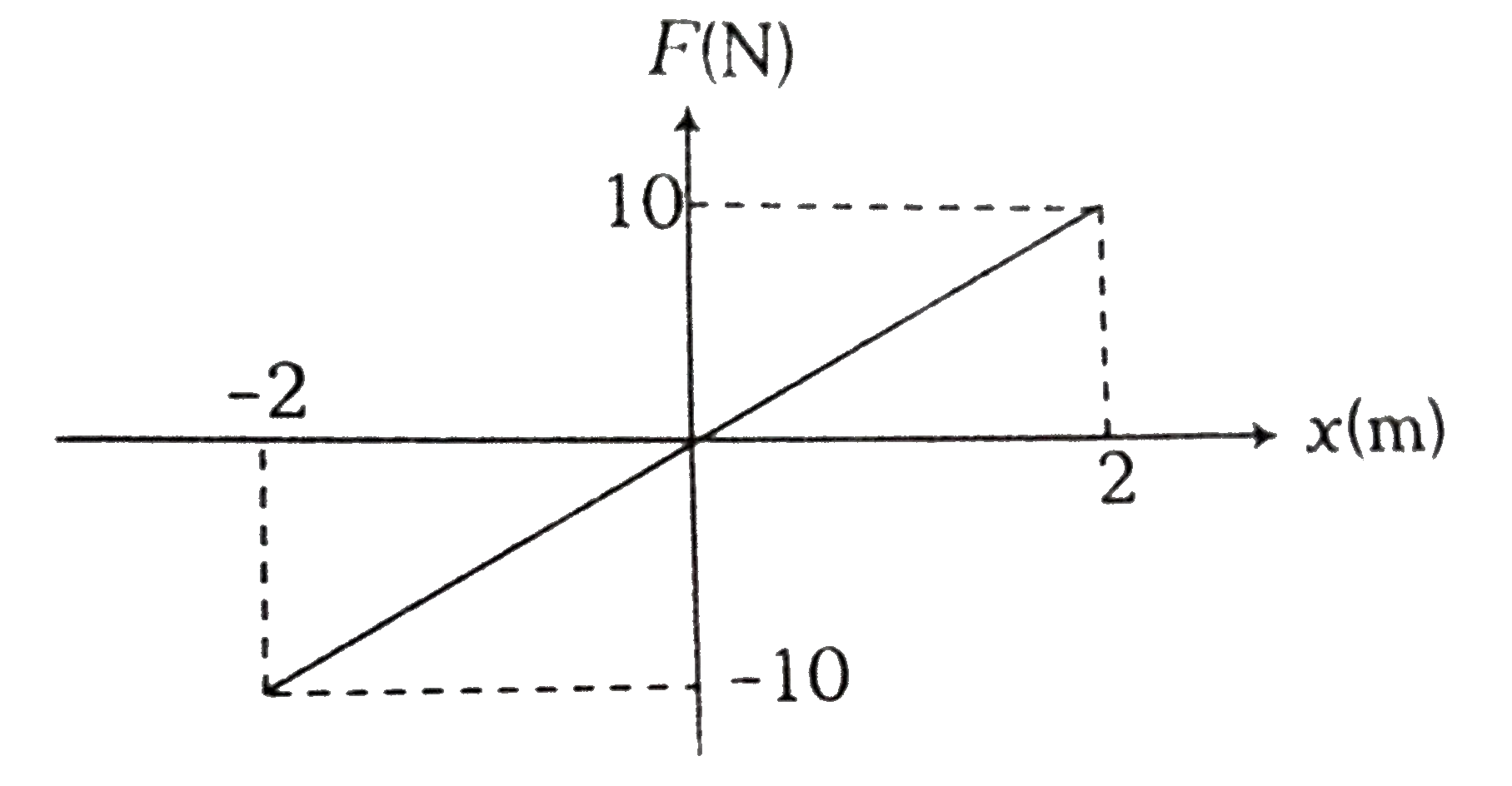
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
View Solution
