A simple pendulum is oscillating without damiping, When the displacement of the bob is less than maximum, its acceleration vector is correctly show in:
(a)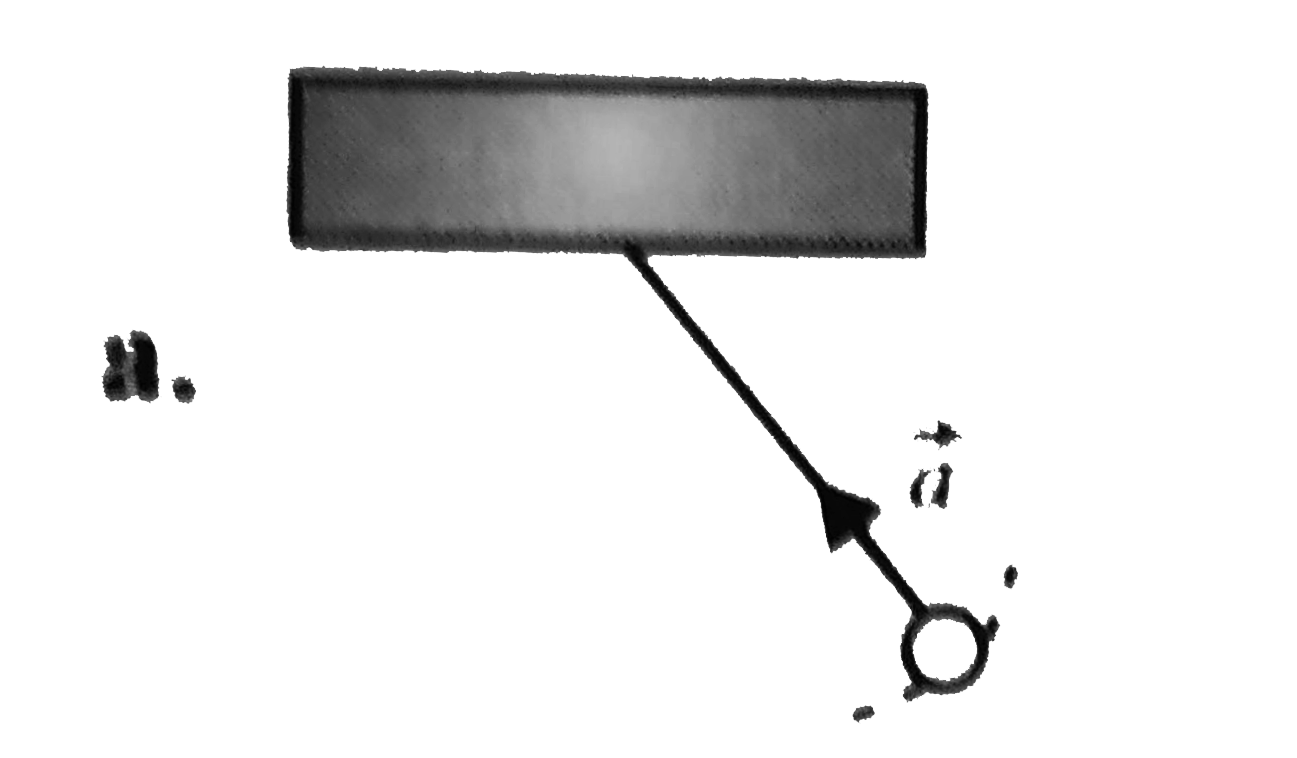 
(b)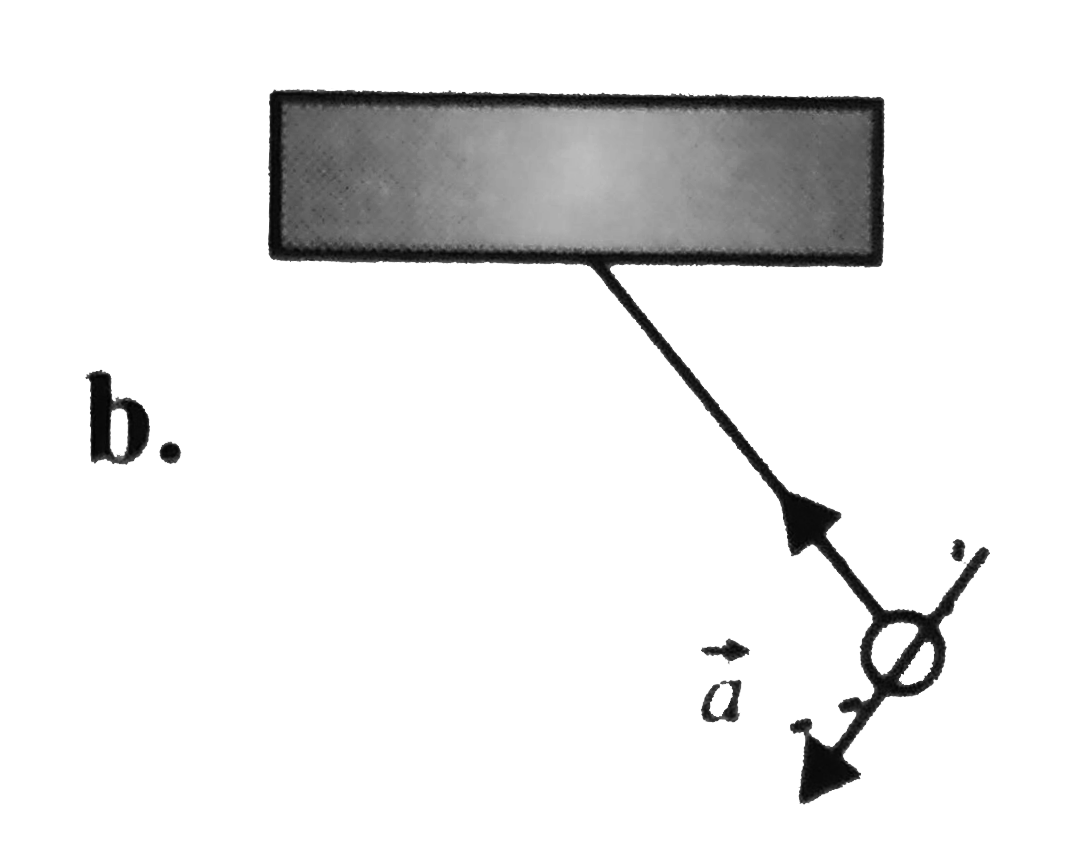 
(c)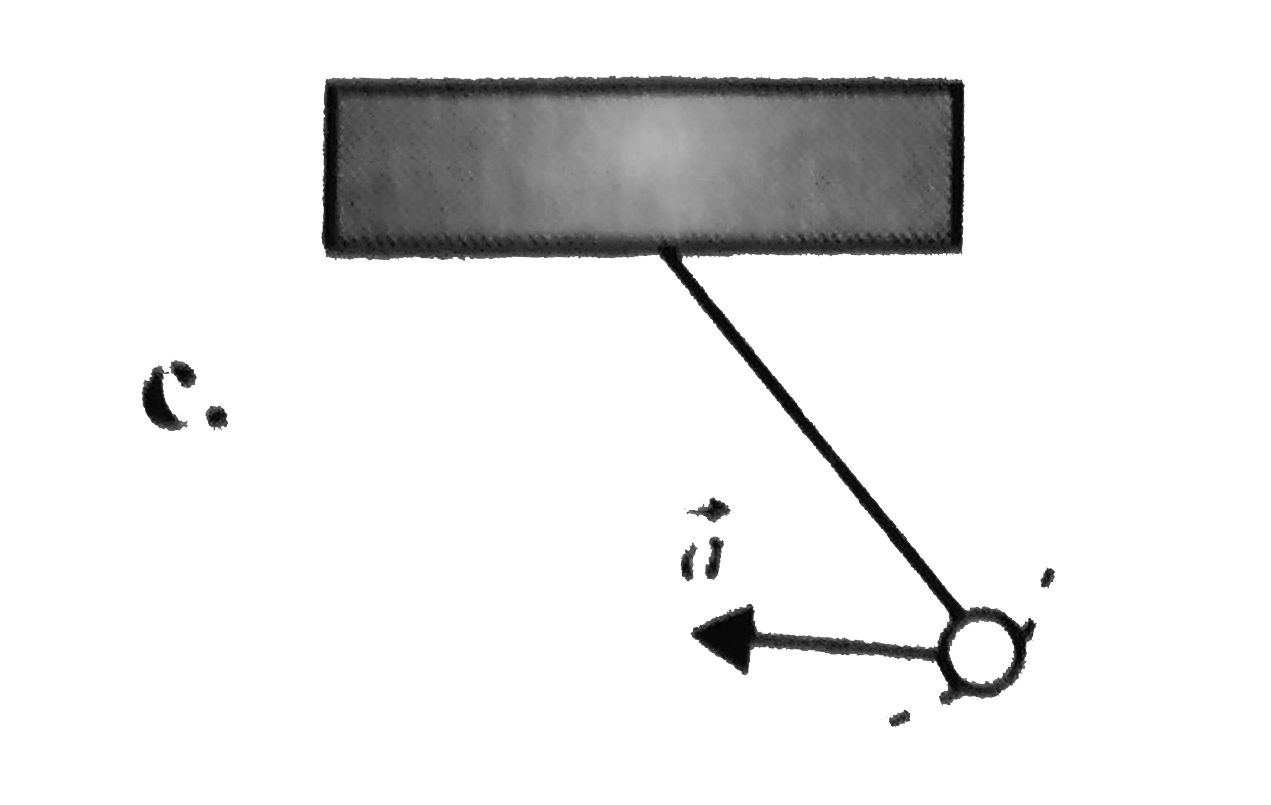 
(d)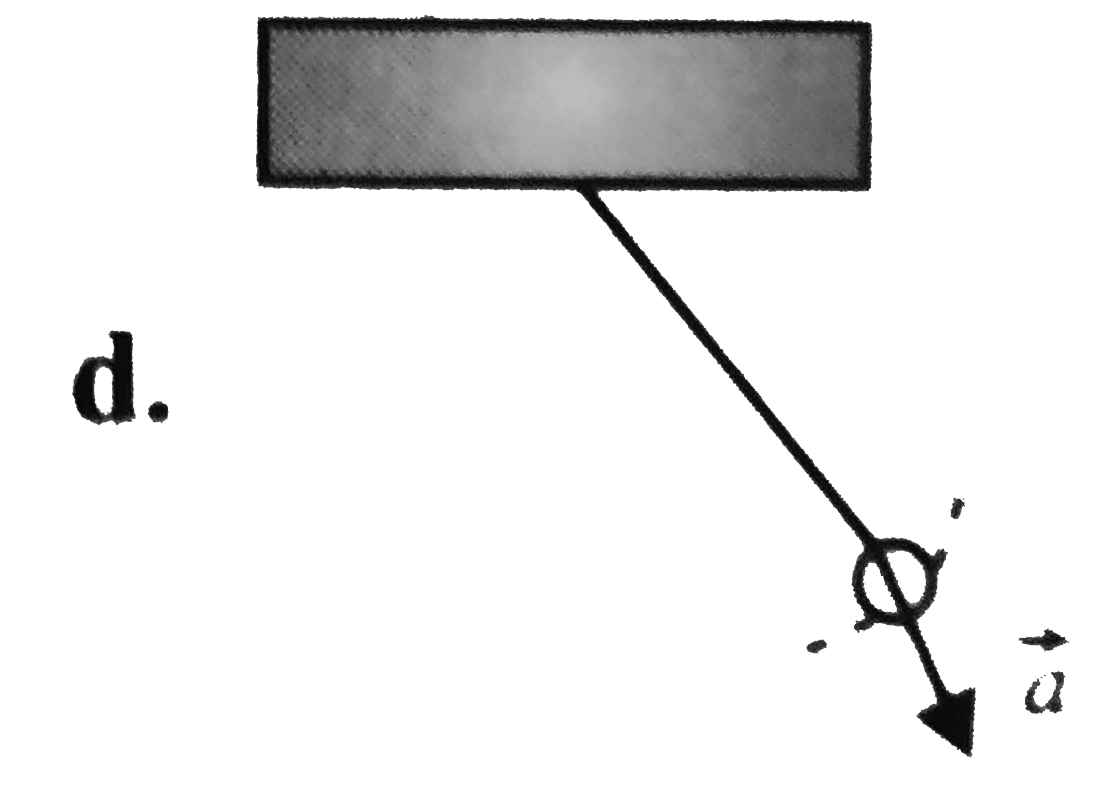 
The correct Answer is:C
Net acceleration of the bob in position B has two components.
a. =radial acceleration (towards BA)
b. = tangential acceleration (perpendicular to BA)
Therefore, direction of is correctly shown in option c.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (assertion-reasoning)
1 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
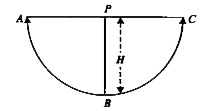AzeroB2g HCmghD√(2gH)
A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum ,while oscillating ,rises to a maximum vertical height of 5 cm from its rest position when it reaches to its extreme position on one side.If mass of the bob of the simple pendulum is 500 g and g-10 m s−2 find :
(i)the total energy of simple pendulum at any instant while oscillating ,and
(ii)the velocity of bob at its mean position State the assumption made in your calculation .
View SolutionThe total energy of a simple pendulum is x. When the displacement is half of amplitude,its KE will be
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionThe time period Of oscillation of a simple pendulum depends on the following quantities
Length of the pendulum (l),
Mass of the bob (m), and
Acceleration due to gravity (g)
Derive an expression for Using dimensional method.
View Solution