A block of mass m is kept on a rough plank which moves with a horizontal acceleration a. If the plank was at rest at t=0, and the block does not slide relative to the plank, find the work done by friction on the (a) block, (b) plane, (c) system, (block+plank) during time t.
To solve the problem step-by-step, we will analyze each part of the question regarding the work done by friction on the block, the plank, and the system as a whole.
Given:
- Mass of the block = m
- Acceleration of the plank = a
- Time = t
Part (a): Work done by friction on the block
1. Identify Forces Acting on the Block:
- The block experiences a frictional force fs acting in the direction of the plank's acceleration.
- The acceleration of the block is equal to the acceleration of the plank, which is a.
2. Calculate the Frictional Force:
- The frictional force fs can be calculated using Newton's second law:
fs=m⋅a
3. Calculate the Displacement of the Block:
- Since the plank starts from rest and accelerates uniformly, we can use the equation of motion to find the displacement s:
s=ut+12at2
- Here, u=0 (initial velocity), so:
s=12at2
4. Calculate Work Done by Friction on the Block:
- The work done by friction Wb is given by:
Wb=fs⋅s
- Substituting the values:
Wb=(m⋅a)⋅(12at2)=12ma2t2
Part (b): Work done by friction on the plank
1. Work Done by the Plank:
- The work done by the plank on the block is equal in magnitude but opposite in direction to the work done by friction on the block. Hence:
Wp=−Wb=−12ma2t2
Part (c): Work done on the system (block + plank)
1. Total Work Done on the System:
- The total work done on the system is the sum of the work done on the block and the work done on the plank:
Wsystem=Wb+Wp
- Substituting the values:
Wsystem=12ma2t2−12ma2t2=0
Final Answers:
- (a) Work done by friction on the block: 12ma2t2
- (b) Work done by friction on the plank: −12ma2t2
- (c) Work done on the system: 0
- Mass of the block = m
- Acceleration of the plank = a
- Time = t
- The block experiences a frictional force fs acting in the direction of the plank's acceleration.
- The acceleration of the block is equal to the acceleration of the plank, which is a.
- The frictional force fs can be calculated using Newton's second law:
fs=m⋅a
- Since the plank starts from rest and accelerates uniformly, we can use the equation of motion to find the displacement s:
s=ut+12at2
- Here, u=0 (initial velocity), so:
s=12at2
- The work done by friction Wb is given by:
Wb=fs⋅s
- Substituting the values:
Wb=(m⋅a)⋅(12at2)=12ma2t2
- The work done by the plank on the block is equal in magnitude but opposite in direction to the work done by friction on the block. Hence:
Wp=−Wb=−12ma2t2
- The total work done on the system is the sum of the work done on the block and the work done on the plank:
Wsystem=Wb+Wp
- Substituting the values:
Wsystem=12ma2t2−12ma2t2=0
- (a) Work done by friction on the block: 12ma2t2
- (b) Work done by friction on the plank: −12ma2t2
- (c) Work done on the system: 0
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A small block of mass m is kept on a rough inclined surface of inclination θ fixed in a car. The car moves with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be
_PHY_E05_250_Q01.png)
View SolutionA block of mass m is pressed against a wall which is moving with an acceleration a as shown in figure If the block is pulled at an angle θ with downward vertical by a force F and it does not slide relative to the wall . Find the
a. friction force between the block and wall
b.inimum magnitude of F so as to cayse a relative sliding between the block and wall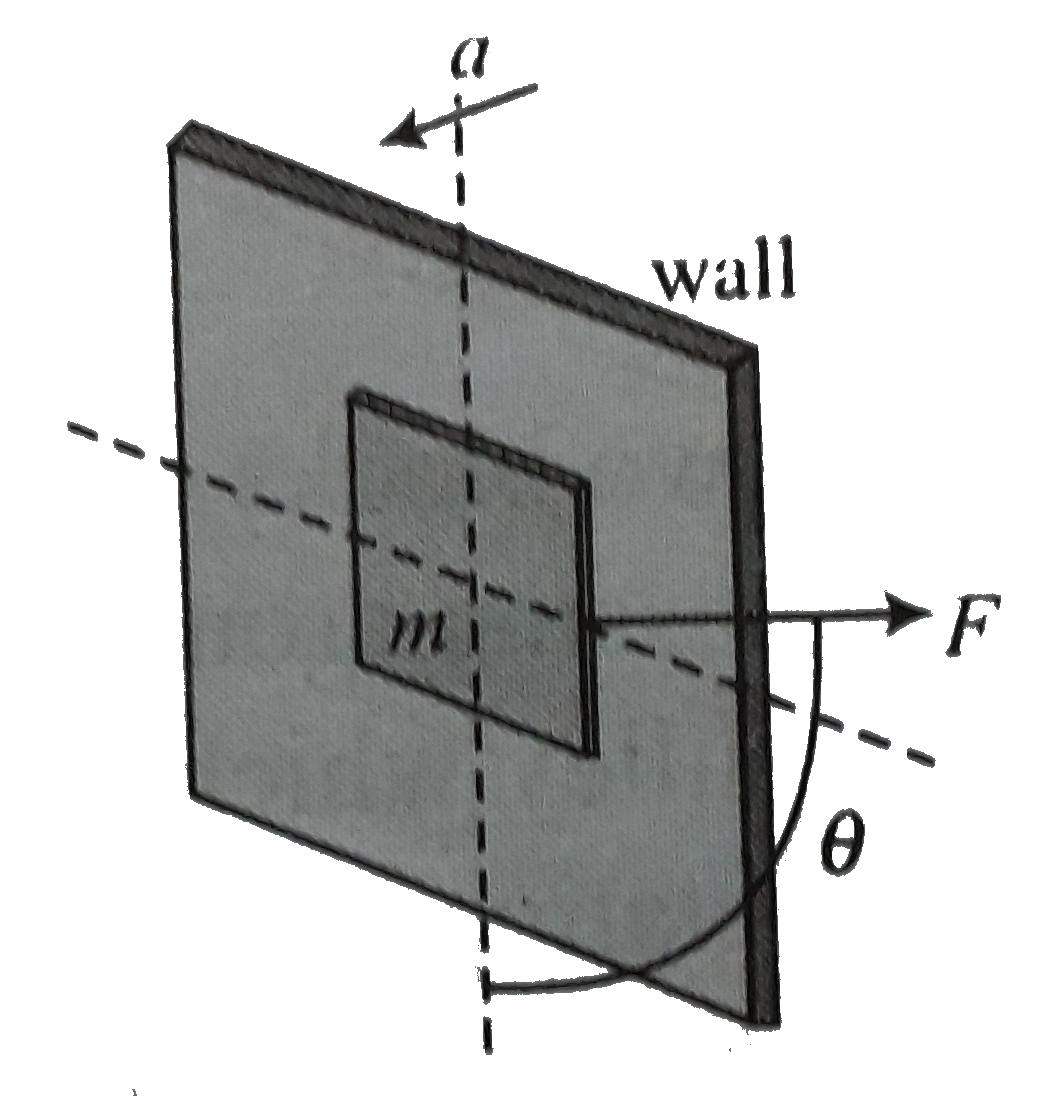
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is placed on the block of mass M as shown in figure. The horizontal force →F acts on M during time interval t. If the horizontal surface is smooth, assuming no relative sliding between the blocks, find the
a. work done by friction on the blocks
b. work done by →F on the lower block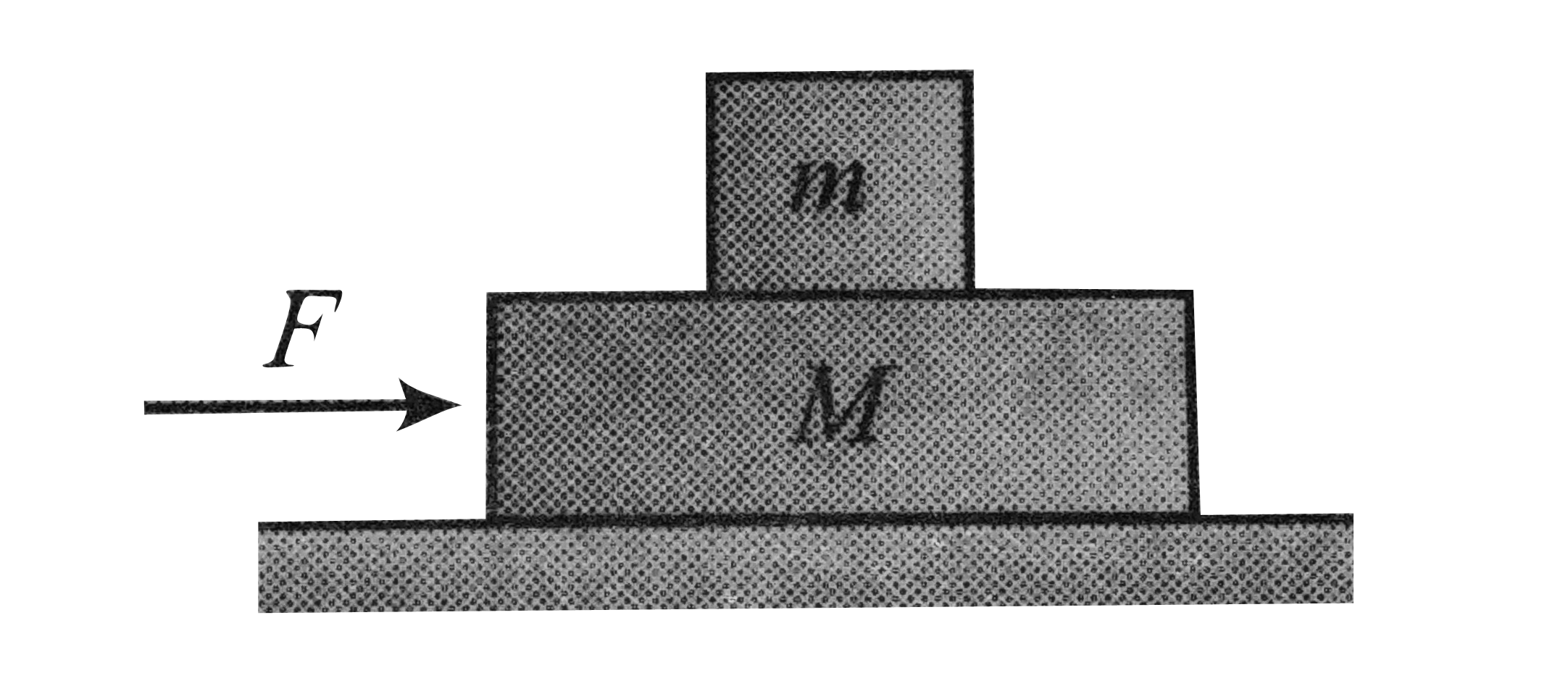
View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
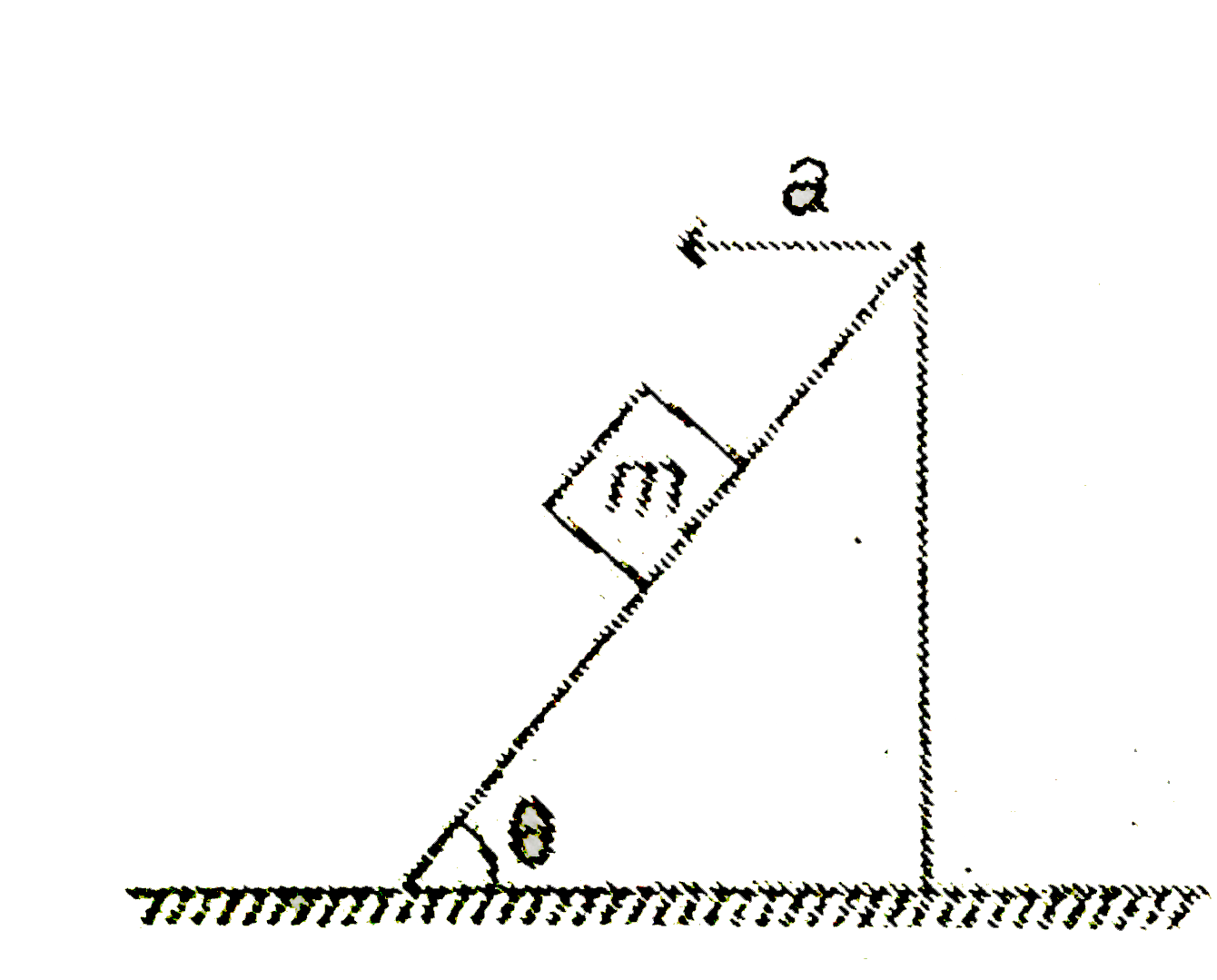
View SolutionA block of mass m=1/3 kg is kept on a rough horizontal plane. Friction coefficient is μ=0.75. The work done by minimum force required to drag to the block along the plane by a distance 5m is :-
View SolutionA block of mass 5 kg is placed on a plank of mass 10 kg which is placed on the smooth horizontal surface as shown in figure. If a 100 N force is applied on the plank then the acceleration of the plank wrt ground is (Coefficient of friction between block and plank μs=μk=0.4 and g=10ms2)
View SolutionA plank of mass 5 kg in kept on a smooth surface. A block of 1 kg is kept on it and is given a velcoity of 12 m/s. There is friction between the block and the plank. Assuming the plank to be very long, find the magnitude of work done (in Joules) by friction on block till the relative sliding between them stops.

View Solution