A force F is exerted on a body of mass M, which is connected to a spring (spring constant k). The body has a constant acceleration a. Calculate the work done by the external force in moving the body by a distance D.
To solve the problem of calculating the work done by the external force in moving a body of mass M connected to a spring with spring constant k, while the body experiences a constant acceleration a over a distance D, we can follow these steps:
Step 1: Understand the Forces Acting on the Body
The external force F is applied to the body. The body is also subjected to the restoring force of the spring, which is given by Hooke's law as Fspring=kx, where x is the displacement of the spring from its equilibrium position.
Step 2: Write the Equation of Motion
Using Newton's second law, the net force acting on the body can be expressed as:
Fnet=F−kx=Ma
Where:
- F is the external force,
- kx is the spring force acting in the opposite direction,
- M is the mass of the body,
- a is the constant acceleration.
Step 3: Rearrange the Equation
From the equation of motion, we can rearrange it to find the external force:
F=Ma+kx
Step 4: Calculate the Work Done by the External Force
The work done W by the external force when moving the body a distance D can be calculated using the formula:
W=∫D0Fdx
Substituting the expression for F:
W=∫D0(Ma+kx)dx
Step 5: Evaluate the Integral
Now we can evaluate the integral:
W=∫D0(Ma)dx+∫D0(kx)dx
Calculating each part:
1. For the first integral:
∫D0(Ma)dx=Ma⋅D
2. For the second integral:
∫D0(kx)dx=k2x2∣∣D0=kD22
Step 6: Combine the Results
Adding both parts together gives us the total work done by the external force:
W=MaD+kD22
Final Answer
Thus, the work done by the external force in moving the body by a distance D is:
W=MaD+kD22
The external force F is applied to the body. The body is also subjected to the restoring force of the spring, which is given by Hooke's law as Fspring=kx, where x is the displacement of the spring from its equilibrium position.
Using Newton's second law, the net force acting on the body can be expressed as:
Fnet=F−kx=Ma
Where:
- F is the external force,
- kx is the spring force acting in the opposite direction,
- M is the mass of the body,
- a is the constant acceleration.
From the equation of motion, we can rearrange it to find the external force:
F=Ma+kx
The work done W by the external force when moving the body a distance D can be calculated using the formula:
W=∫D0Fdx
Substituting the expression for F:
W=∫D0(Ma+kx)dx
Now we can evaluate the integral:
W=∫D0(Ma)dx+∫D0(kx)dx
Calculating each part:
1. For the first integral:
∫D0(Ma)dx=Ma⋅D
2. For the second integral:
∫D0(kx)dx=k2x2∣∣D0=kD22
Adding both parts together gives us the total work done by the external force:
W=MaD+kD22
Thus, the work done by the external force in moving the body by a distance D is:
W=MaD+kD22
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A force is applied on a body of mass 20 kg moving with a velocity of 40ms−1. The body attains a velocity of 50ms−1 in 2 second. Calculate the work done by the body.
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
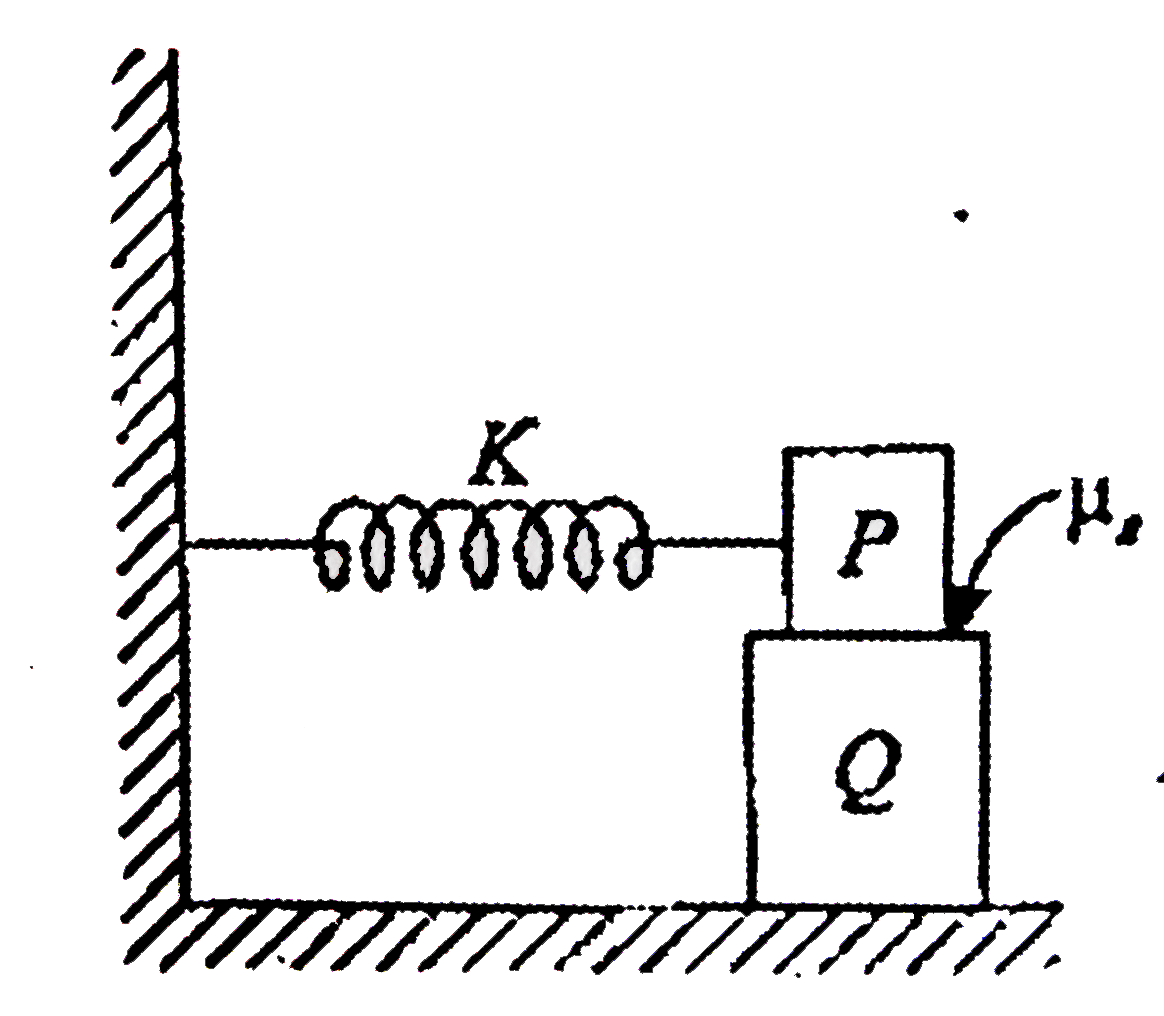
View Solution
Knowledge Check
A body of mass m is moving in a circle of radius r with a constant speed v. The work done by the centripetal force in moving the body over half the circumference of the circle is
Amv2/rBzeroCmv2/rDr2/mv2A body constrained to move along y-axis is subjected to a constant force →F=−ˆi+2ˆj+3ˆkN. The work done by this force in moving the body a distance of 4 m along y-axis is
A4JB8 JC12JD24 JA body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA body constrained to move along y-axis is subjected to a constant force →F=−ˆi+2ˆj+3ˆkN. The work done by this force in moving the body a distance of 4 m along y-axis is
View SolutionForce constant of a spring (k) is anonymous to
View SolutionThe work done by a body is the product of force and
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
