A force →F=(3xN)ˆi+(4N)ˆj, with x in meter, acts on a particle, changing only the kinetic energy of the particle. How mcuh work is done on the particle as it moves from coordinates (2m,3m,5m) to (3m,0m,6m)? Does the speed of the particle increase, decrease, or remain the same?
To solve the problem, we need to calculate the work done on the particle as it moves from the initial coordinates (2m, 3m, 5m) to the final coordinates (3m, 0m, 6m) under the influence of the force →F=(3xN)^i+(4N)^j.
1. Identify the Force Components:
The force acting on the particle is given as:
→F=(3x)^i+(4)^j
Here, x is the x-coordinate of the particle.
2. Determine the Path of Motion:
The particle moves from the point (2,3,5) to (3,0,6). The change in coordinates is:
- From x=2 to x=3
- From y=3 to y=0
- The z-coordinate changes from z=5 to z=6 but does not affect the work done since the force has no z-component.
3. Calculate Work Done:
The work done W by the force as the particle moves is given by the line integral:
W=∫→F⋅d→r
We can break this integral into two parts, one for the x-component and one for the y-component.
- For the x-component:
Wx=∫x=3x=2(3x)dx
Wx=(3x22)32=3(32)2−3(22)2=3(9)2−3(4)2=272−122=152=7.5J
- For the y-component:
Wy=∫y=0y=3(4)dy
Wy=4∫03dy=4(y)03=4(0−3)=−12J
- Total Work Done:
W=Wx+Wy=7.5J−12J=−4.5J
4. Determine the Change in Kinetic Energy:
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy:
W=ΔKE
Since W=−4.5J, this means the kinetic energy of the particle decreases by 4.5 J.
5. Conclusion about Speed:
Since the kinetic energy of the particle decreases, the speed of the particle must also decrease.
Final Answer:
The work done on the particle is −4.5J, and the speed of the particle decreases.
The force acting on the particle is given as:
→F=(3x)^i+(4)^j
Here, x is the x-coordinate of the particle.
The particle moves from the point (2,3,5) to (3,0,6). The change in coordinates is:
- From x=2 to x=3
- From y=3 to y=0
- The z-coordinate changes from z=5 to z=6 but does not affect the work done since the force has no z-component.
The work done W by the force as the particle moves is given by the line integral:
W=∫→F⋅d→r
We can break this integral into two parts, one for the x-component and one for the y-component.
Wx=∫x=3x=2(3x)dx
Wx=(3x22)32=3(32)2−3(22)2=3(9)2−3(4)2=272−122=152=7.5J
Wy=∫y=0y=3(4)dy
Wy=4∫03dy=4(y)03=4(0−3)=−12J
W=Wx+Wy=7.5J−12J=−4.5J
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy:
W=ΔKE
Since W=−4.5J, this means the kinetic energy of the particle decreases by 4.5 J.
Since the kinetic energy of the particle decreases, the speed of the particle must also decrease.
The work done on the particle is −4.5J, and the speed of the particle decreases.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.326videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A force →F=(3ˆi+4ˆj) N is acting on a particle. Work done by the force is zero, when particle is moving on the line 2y+Px=2, the value of P is
View SolutionA force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its original position to the point →s=S(2ˆi−1ˆj)m. The work done on the particle is
View Solution
Knowledge Check
- Question 1 - Select One
A varable force, given by the 2- dimensional vector¯¯¯F=(3×2ˆi+4ˆj), acts on a particle. The force is in newton and x is in metre. What is the change in the kinetic energy of the particle as it moves from the point with coordinates (2,3) to (3,0) (The coornates are in metres)
A−7JBzeroC+7JD+19J
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
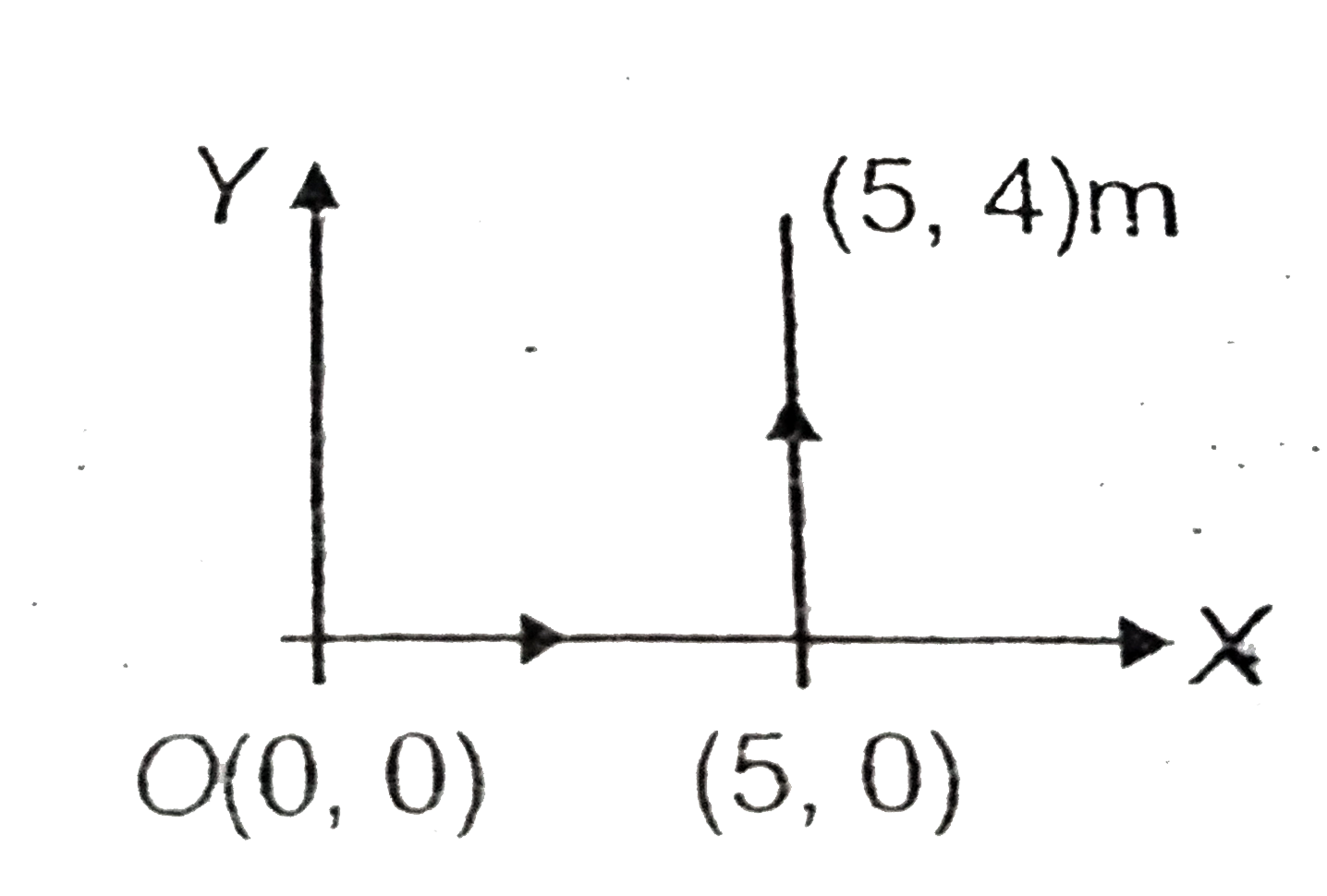 View Solution
View SolutionA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
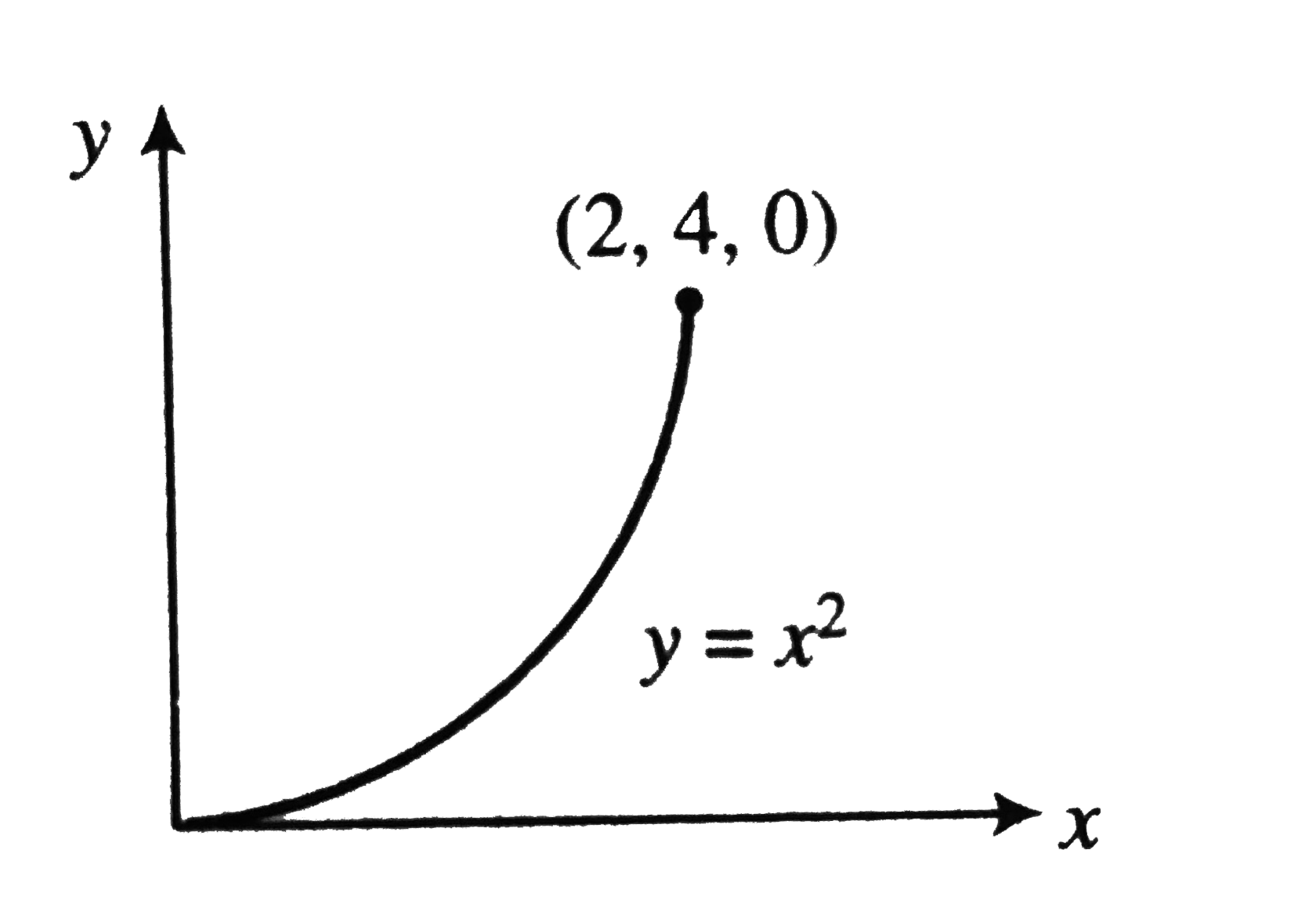 View Solution
View SolutionForce on a particle varies with position (x) of particle as shown, calculate work done by force from x=0 to x=30 m.
 View Solution
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA Force F = (2ˆi+ˆj+3ˆk) N acts on a particle of mass 1 kg for 2 s . If initial velocity of particle is u = (2ˆi+ˆj) m/s . Speed of particle at the end of 2 s will be
View SolutionA particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
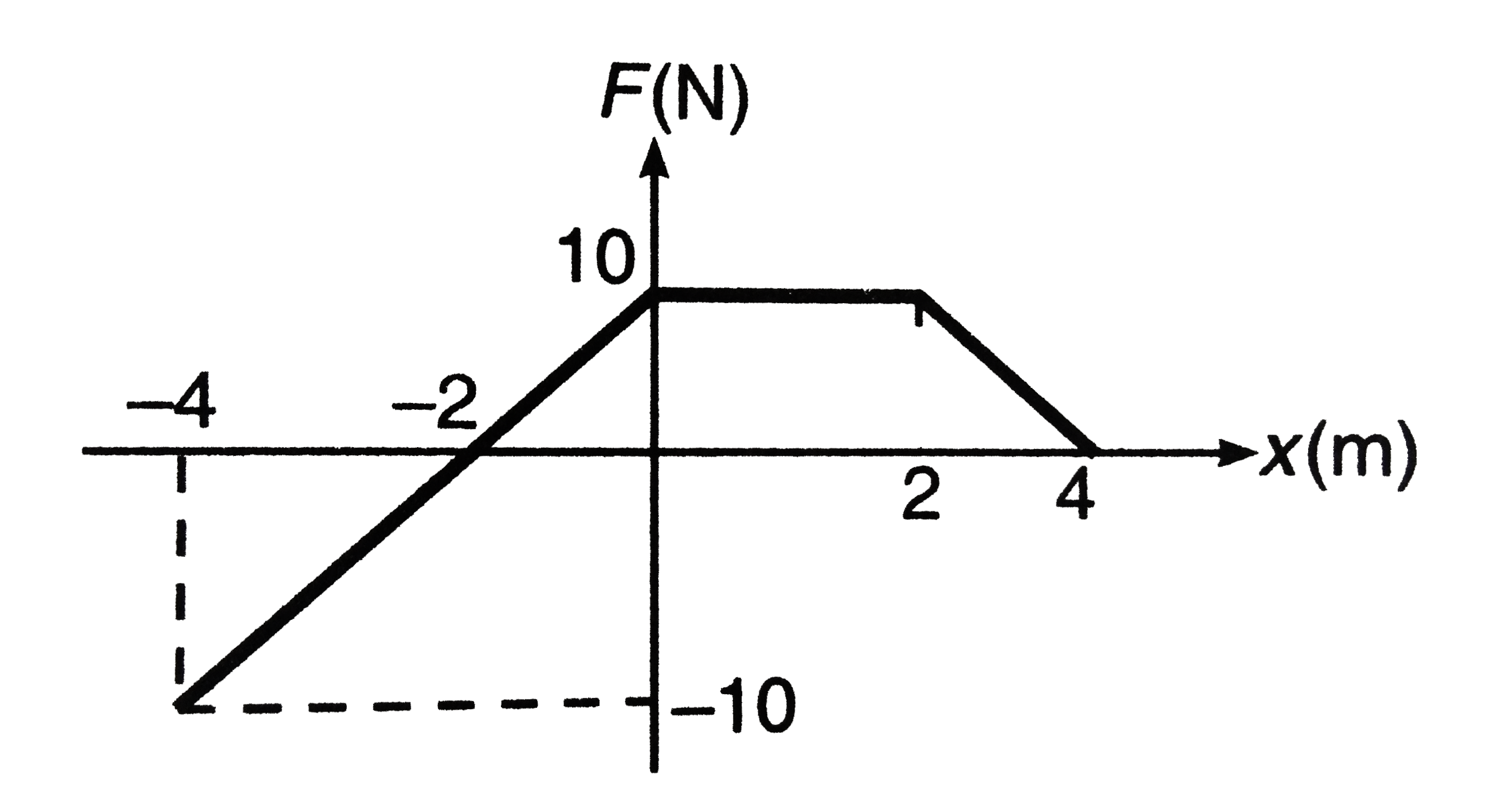 . View Solution
. View Solution
