A person sitting in the rear end of the compartment throws a ball towards the front end. The ball follows a parabolic path. The train is moving with uniform velocity of 20ms−1. A person standing outside on the ground also observers the ball. How will the maximum heights (hm) attained and the ranges (R) seen by thrower and the outside observer compare each other?
Same hm, differect R
same hm, and R
different hm, same R
different hm, and R
The correct Answer is:A
To solve the problem, we need to analyze the motion of the ball as observed by both the person sitting in the train and the observer on the ground.
Step 1: Understand the Motion of the Ball
The ball is thrown from the rear end of the train towards the front end. The train is moving with a uniform velocity of 20m/s. The ball follows a parabolic path due to the influence of gravity.
Step 2: Define the Velocity Components
Let’s denote the velocity of the ball with respect to the train as:
- vx (horizontal component)
- vy (vertical component)
The velocity of the train is 20m/s in the horizontal direction.
Step 3: Velocity of the Ball with Respect to the Ground
The velocity of the ball with respect to the ground can be expressed as:
- vx,ground=vx+20
- vy,ground=vy
Step 4: Maximum Height Calculation
The maximum height hm attained by the ball depends solely on the vertical component of the initial velocity vy. The formula for maximum height is given by:
hm=v2y2g
where g is the acceleration due to gravity. Since vy is the same for both observers (the thrower and the observer on the ground), the maximum height hm will be the same for both.
Step 5: Range Calculation
The horizontal range R of the ball is influenced by the horizontal component of the velocity. The time of flight t can be determined from the vertical motion:
t=2vyg
The range for the thrower in the train is:
Rtrain=vx⋅t
For the observer on the ground, the range is:
Rground=(vx+20)⋅t
Since the horizontal component of the velocity is different for the two observers, the ranges will differ.
Conclusion
- The maximum height hm attained by the ball is the same for both the thrower and the observer on the ground.
- The range R seen by the thrower and the observer will be different due to the additional velocity of the train.
Final Answer
The maximum heights hm are the same, but the ranges R are different.
The ball is thrown from the rear end of the train towards the front end. The train is moving with a uniform velocity of 20m/s. The ball follows a parabolic path due to the influence of gravity.
Let’s denote the velocity of the ball with respect to the train as:
- vx (horizontal component)
- vy (vertical component)
The velocity of the ball with respect to the ground can be expressed as:
- vx,ground=vx+20
- vy,ground=vy
The maximum height hm attained by the ball depends solely on the vertical component of the initial velocity vy. The formula for maximum height is given by:
hm=v2y2g
where g is the acceleration due to gravity. Since vy is the same for both observers (the thrower and the observer on the ground), the maximum height hm will be the same for both.
The horizontal range R of the ball is influenced by the horizontal component of the velocity. The time of flight t can be determined from the vertical motion:
t=2vyg
The range for the thrower in the train is:
Rtrain=vx⋅t
For the observer on the ground, the range is:
Rground=(vx+20)⋅t
Since the horizontal component of the velocity is different for the two observers, the ranges will differ.
- The maximum height hm attained by the ball is the same for both the thrower and the observer on the ground.
- The range R seen by the thrower and the observer will be different due to the additional velocity of the train.
The maximum heights hm are the same, but the ranges R are different.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A platform is moving upwards with a constant acceleration of 2ms−2. At time t=0, a boy standing on the platform throws a ball upwards with a relative speed of 8ms−1. At this instant, platform was at the height of 4m from the ground and was moving with a speed of 2ms−1. Take g=0ms−2. Find
(a) when and where the ball strikes the platform.
(b) the maximum height attained by the ball from the ground.
( c) the maximum distance of the ball from the platform.
View SolutionTwo balls of equal mass are projected upwards simultaneously, one from the ground with initial velocity 50ms−1 and the other from a 40m tower with initial velocity of 30ms−1. The maximum height attained by their COM will be a) 80 m b) 60 m c) 100 m d) 120 m
View SolutionA ball is projected with the velocity an angle of θ and (90°-θ) with horizontal.If h1 and h2 are maximum heights attained by it in two paths and R is the range of a projectile, then which of the following relation is correct
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would be
View SolutionA person drops a stone from a building of height 20 m. At the same instant the front end of a truck passes below the building moving with constant acceleration of 1m/s2 and velocity of 2m/s at that instant. Length of the truck if the stone just misses to hit its rear part is :-
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
4. The maximum separation between the floor of elevator and the ball during its flight would be
View SolutionA man is standing on a rail road car travelling with a constant speed of v=10ms−1 (Fig . 5.34). He wishes to throw a ball through a stationary hoop 5m above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of 12.5ms−1 w.r.t. himself.
(a) What must be the vertical component of the initial velocity of the ball ?
(b) How many seconds after he releases the ball will it pass through the hoop ?
( c) At what horizontal distance in front of the loop must he release the ball ?
 .
.
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
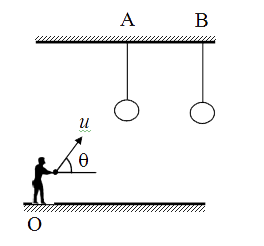
The maximum height attained by the ball above the floor is:
View SolutionA man throws a ball of mass m from a moving plank (A). The ball has a horizontal component of velocity u=3√34ms−1 with respect to ground towards another man standing on stationary plank (B), as shown in the figure. The combined mass of plank A with man is 2m each. The x-y plane represents the horizontal plane which is frictionless. If initially, plank A was moving with speed uˆi with respect to ground, then the relative velocity of plank B (in m s−1) with respect to plank A (after the man on plank B catches the ball) minus 10ms−1 is

View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student speculates that the constant C depends on :-
(i) The angle at which the ball was launched (ii) The ball's mass (iii) The ball's diameter
If we neglect air resistance, then C actually depends on :-
View Solution