A rifle shoots a bullet with a muzzle velocity of 400ms−1 at a small target 400m away. The height above the target at which the bullet must be aimed to hit the target is (g=10ms−2).
1 m
5 m
10 m
0.5 m
The correct Answer is:B
To solve the problem of how high above the target the bullet must be aimed to hit a target 400 m away, we can follow these steps:
Step 1: Understand the Problem
We need to find the height h above the target where the rifle must be aimed. The bullet is fired with a muzzle velocity u=400m/s and the target is at a horizontal distance R=400m.
Step 2: Use the Range Formula
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity. In this case, g=10m/s2.
Step 3: Substitute Known Values
Substituting the known values into the range formula:
400=(400)2sin(2θ)10
This simplifies to:
400=160000sin(2θ)10
400=16000sin(2θ)
Dividing both sides by 16000 gives:
sin(2θ)=40016000=140
Step 4: Approximate for Small Angles
For small angles, we can use the approximation sin(2θ)≈2θ. Therefore:
2θ≈140
This implies:
θ≈180radians
Step 5: Relate Height to Angle
The height h above the target can be related to the angle θ using the tangent function:
tan(θ)=hR
For small angles, tan(θ)≈θ. Thus:
h400≈180
Step 6: Solve for Height h
Now, we can solve for h:
h≈400⋅180=5m
Conclusion
The height above the target at which the bullet must be aimed is h=5m.
We need to find the height h above the target where the rifle must be aimed. The bullet is fired with a muzzle velocity u=400m/s and the target is at a horizontal distance R=400m.
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where g is the acceleration due to gravity. In this case, g=10m/s2.
Substituting the known values into the range formula:
400=(400)2sin(2θ)10
This simplifies to:
400=160000sin(2θ)10
400=16000sin(2θ)
Dividing both sides by 16000 gives:
sin(2θ)=40016000=140
For small angles, we can use the approximation sin(2θ)≈2θ. Therefore:
2θ≈140
This implies:
θ≈180radians
The height h above the target can be related to the angle θ using the tangent function:
tan(θ)=hR
For small angles, tan(θ)≈θ. Thus:
h400≈180
Now, we can solve for h:
h≈400⋅180=5m
The height above the target at which the bullet must be aimed is h=5m.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A bulley with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
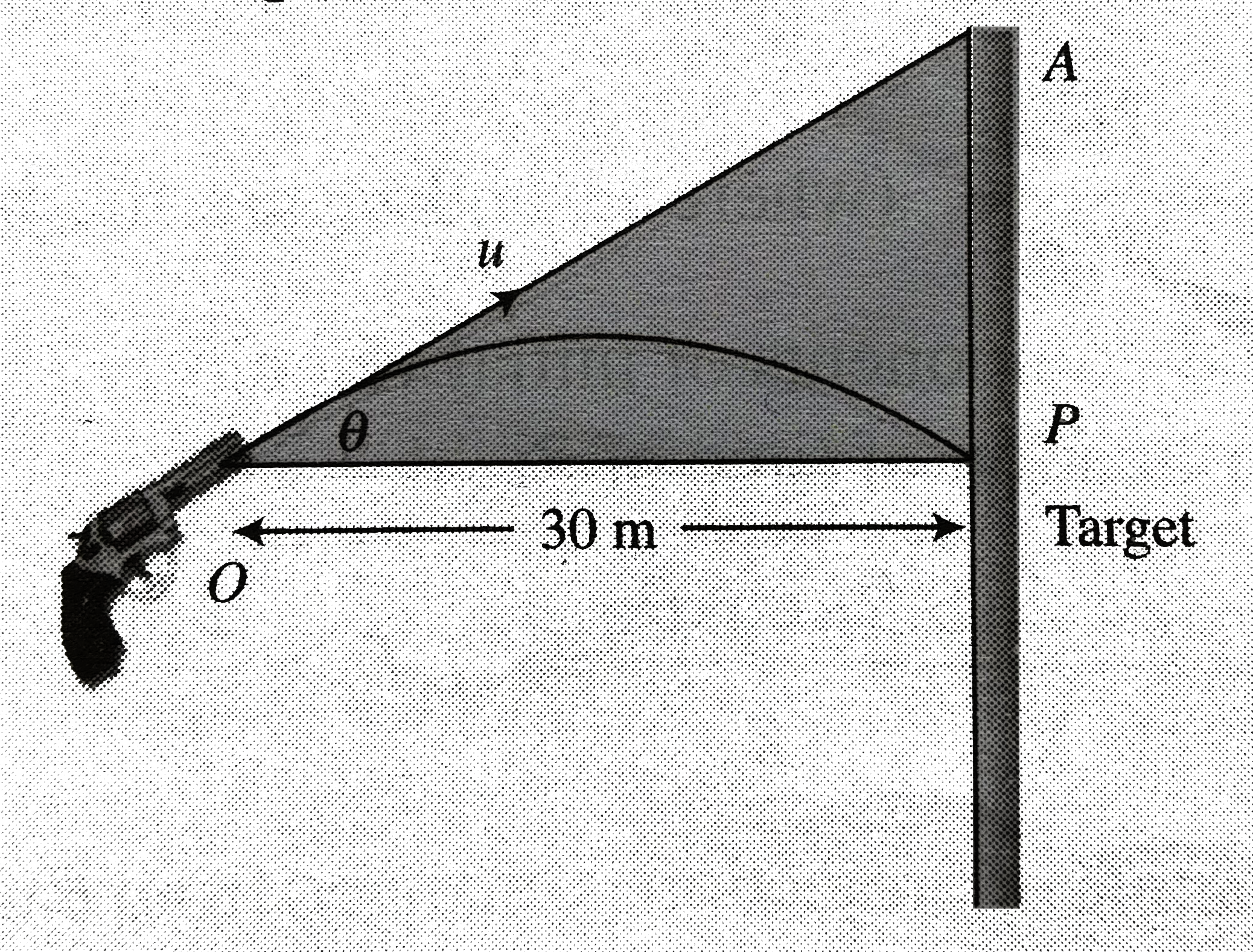 .
.
View SolutionA bullet is fired from a gun eith a speed of 1000m/s on order to hit target 100 m away At what height above target should the gun be aimed ? (The resistance of air is negligible and g = 10 m/s2)
View SolutionThe initial speed of a bullet fired from a rifle is 630 m/s. . The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of target, the rifle must be aimed in order to hit the target?
View SolutionA bullet is to be fired with a speed of 2000m/s to hit a target 200m away on a level ground. If g=10m/s2, the gun should be aimed
View SolutionA bullet moving with a velocity of 30√2ms−1 is fired into a fixed target. It penetrated into the target to the extent of s metres. If the same bullet is fired into a target of thickness s2 metres and of the same material with the same velocity, then the bullet comes out of the target with velocity
View SolutionA bullet initially moving with a velocity 20 m s−1 strikes a target and comes to rest after penetrating a distance 10 cm in the target. Calculate the retardation caused by the target.
View SolutionA 2 g bullet moving with a velocity of 200 m/s is brought to a sudden stoppage by an obstacle. The total heat produced goes to the bullet. If the specific heat of the bullet is 0.03cal/g∘C, the rise in its temperature will be
View SolutionA jet aeroplane is flying at a constant height of 2 km with a speed 360kmh−1 above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g=10ms−2)
View SolutionAn aeroplane is travelling at a height of 2000 m from the ground. The aeroplane, when at a point P, drops a bomb to hit a stationary target Q on the ground. In order that the bomb hits the target, what angle θ must the line PQ make with the vertical? [g=10ms−2]

View SolutionA person holding a rifle (mass of person and rifle together is 100 kg) stands on a smooth surface and fires 10 shots horizontally, in 5s. Each bullet has a mass of 10 g with a muzzle velocity of 800 ms−1. The final velocity acquired by the person and the average force exerted on the person are
View Solution

