Two particle are projected with same initial velocities at an angle $30^{\circ}$ and $60^{\circ}$ with the horizontal .Then

Video Solution

Text Solution

Verified by Experts

Method 1 : Foe bullet A. Let $t$ be the time taken by bullet $A$ to reach $P$
Vertical motion : $u_{y} = 0, S = u t + \frac{1}{2} a t^{2}, S_{y} = - (10 - y)$
$a_{y} = - 10 m s^{- 2} \Rightarrow 10 - y = 5 t^{2}$ …(i)
Horizontal motion : $x = 5 \sqrt{3} t$ …(ii)
For bullet B. Let $(t + l)$ be the time taken by bullet $B$ to reach $P$ .
Vertical motion : $↑ ⏐ ⏐ + u_{y} = + 5 \sqrt{3} {sin 60}^{\circ} = + 7.5 m s^{- 1}$
$S = u t + \frac{1}{2} a t^{2}, a_{y} = - 10 m s^{- 2}$
$y - 10 = 7.5 (t + t') - 5 {(t + t')}^{2}$ ...(iii)
Horizontal motion : $x = (5 \sqrt{3} {cos 60}^{\circ}) (t + t')$
$\Rightarrow 5 \sqrt{3} t + 5 \sqrt{3} t' = 2 x$ ...(iv)
Substituting the value of $x$ from (ii) in (iv), we get
$5 \sqrt{3} t + 5 \sqrt{3} t' = 10 \sqrt{3}) t \Rightarrow t = t'$
(a) Putting $t = t'$ in (iii),
$y - 10 = 15 t - 20 t^{2}$ ...(v)
Adding (i) and (v), $0 = 15 t - 15 t^{2} \Rightarrow t = 1 s$
So time interval between the firings is $t' = 1 s$
(b) Putting $t - 1$ in (ii), we get $x = s \sqrt{3} m$ .
Putting $t = 1$ in (i), we get $y = 5$ .
Therefore, the coordinates of point
$P a r e (5 (\sqrt{3}, 5))$ in meters.
Method 2 : We take the point of firing as origin and $x - and y$ - axis as shown in (Fig. 5.174). Equation of trajectory of the projectile is
$y = x tan θ - \frac{g x^{2}}{2 v_{i}^{2} {cos}^{2} θ}$
For gun 1, $θ = 60^{\circ}$ . Therefore,
$y = x {tan 60}^{\circ} - \frac{g x^{2}}{2 v_{i}^{2} {cos}^{2} 60^{\circ}} = x \sqrt{3} - \frac{2 g x^{2}}{v_{i}^{2}}$
For gun 2, $θ = 0^{\circ}$ . Therefore,
$y = \frac{- g x^{2}}{2 v_{i}^{2}}$
Two shots collide at point $P$ . Therefore, their coordinates must be same.
$\frac{- g x^{2}}{2 v_{i}^{2}} = x \sqrt{3} - \frac{2 g x^{2}}{2 v_{i}^{2}}$
$x \sqrt{3} = \frac{2 g x^{2}}{v_{i}^{2}} - \frac{g x^{2}}{2 v_{i}^{2}} = \frac{3 g x^{2}}{2 v_{i}^{2}}$
$x = 0$ and $x = \frac{2 v_{i}^{2}}{\sqrt{3 g} = \frac{2 {(5 \sqrt{3})}^{2}}{\sqrt{3 (10)}} = 5 \sqrt{3}}$
$y = \frac{- g x^{2}}{2 v_{i}^{2}} = \frac{- 10 {(5 \sqrt{3})}^{2}}{2 {(5 \sqrt{3})}^{2}} = - 5 m$
If the origin is assigned at ground, the coordinates of point $P$ will be $(5 \sqrt{3}) m, 5 m)$ .
Now we consider the x - component of displacement for both the shots.
Gun 1 : $x = 5 \sqrt{3} m = v_{i} t (5 \sqrt{3} m s^{- 1}) t$
or $t_{1} = 1 s$
Gun 2 : $x = 5 \sqrt{3} m = v_{i} {cos 60}^{\circ} t_{2} = \frac{5 \sqrt{3}}{2} t_{2}$
or $t_{2} = 2 s$
Time interval between two shots, $Δ t = t_{2} - t_{1} = 1 s$ .
,.

Updated on:21/07/2023

|

Class 11 PHYSICS PROJECTILE MOTION

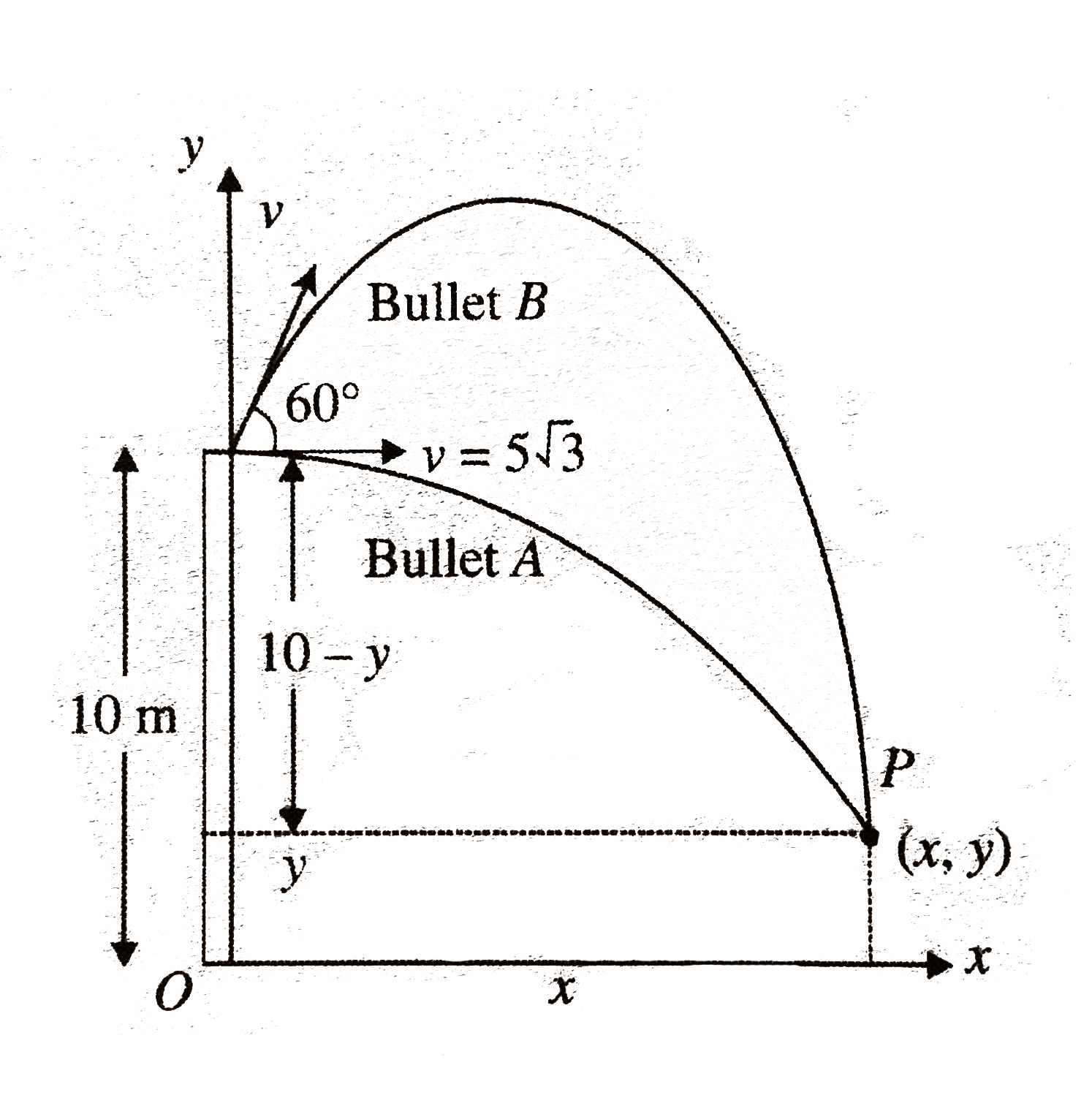Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Solved Examples

Home
Ask Doubt
Profile