Four projectiles are projected with the same speed at angles 20∘,35∘,60∘and75∘
with the horizontal. The range will be the maximum for the projectile whose angle of projection is
(a)20∘
(b)35∘
(c)60∘
(d)75∘
The correct Answer is:B
To determine which projectile has the maximum range, we can use the formula for the range of a projectile, which is given by:
R=v2sin(2θ)g
where:
- R is the range,
- v is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
Since all projectiles are projected with the same speed, we can focus on maximizing sin(2θ).
1. Calculate sin(2θ) for each angle:
- For θ=20∘:
sin(2×20∘)=sin(40∘)
- For θ=35∘:
sin(2×35∘)=sin(70∘)
- For θ=60∘:
sin(2×60∘)=sin(120∘)
- For θ=75∘:
sin(2×75∘)=sin(150∘)
2. Find the values of sin(40∘), sin(70∘), sin(120∘), and sin(150∘):
- sin(40∘)≈0.6428
- sin(70∘)≈0.9397
- sin(120∘)=sin(180∘−60∘)=sin(60∘)≈0.8660
- sin(150∘)=sin(180∘−30∘)=sin(30∘)=0.5
3. Compare the values of sin(2θ):
- sin(40∘)≈0.6428
- sin(70∘)≈0.9397 (maximum)
- sin(120∘)≈0.8660
- sin(150∘)=0.5
4. Conclusion:
The maximum value of sin(2θ) occurs at θ=35∘ with sin(70∘)≈0.9397. Therefore, the projectile with the angle of projection 35∘ will have the maximum range.
Final Answer:
The range will be maximum for the projectile whose angle of projection is 35∘.
- R is the range,
- v is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
- For θ=20∘:
sin(2×20∘)=sin(40∘)
- For θ=35∘:
sin(2×35∘)=sin(70∘)
- For θ=60∘:
sin(2×60∘)=sin(120∘)
- For θ=75∘:
sin(2×75∘)=sin(150∘)
- sin(40∘)≈0.6428
- sin(70∘)≈0.9397
- sin(120∘)=sin(180∘−60∘)=sin(60∘)≈0.8660
- sin(150∘)=sin(180∘−30∘)=sin(30∘)=0.5
- sin(40∘)≈0.6428
- sin(70∘)≈0.9397 (maximum)
- sin(120∘)≈0.8660
- sin(150∘)=0.5
The maximum value of sin(2θ) occurs at θ=35∘ with sin(70∘)≈0.9397. Therefore, the projectile with the angle of projection 35∘ will have the maximum range.
The range will be maximum for the projectile whose angle of projection is 35∘.
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
Knowledge Check
Two projectiles are projected with the same velocity. If one is projected at an angle of 30∘ and the other at 60∘ to the horizontal, then ratio of maximum heights reached, is
A3:1B1:3C1:2D2:1If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
Atan−1(HR)Btan−1(2HR)Ctan−1(4HR)Dtan−1(4HH)
A projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View SolutionTwo projectiles A and B are projected with same speed at an angle 30∘ and 60∘ to the horizontal, then which of the following is not valid where T is total time of flight, H is max height and R is horizontal range.
View SolutionTwo stones are projected with the same speed but making different angles with the horizontal. Their horizontal ranges are equal. The angle of projection of one is π3 and the maximum height reached by it is 102 m. Then the maximum height reached by the other in metres is
View SolutionTwo stones are projected with the same speed but making different angles with the horizontal. Their horizontal ranges are equal. The angle of projection of one is π3 and the maximum height reached by it is 102 m. Then the maximum height reached by the other in metres is
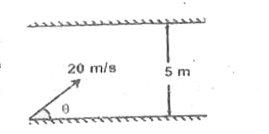
View SolutionA projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
View SolutionThe horizontal range of a projectile is 4√3 times its maximum height. Its angle of projection will be
View Solution
