A body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
8u217g
u22g
16u27g
4u23g
The correct Answer is:A
To solve the problem, we need to find the maximum vertical height of a body projected with velocity u such that the horizontal range and maximum vertical height are equal.
1. Understanding the Equations:
- The formula for the horizontal range R of a projectile is given by:
R=u2sin2θg
- The formula for the maximum height H of a projectile is given by:
H=u2sin2θ2g
2. Setting the Equations Equal:
- According to the problem, the horizontal range and maximum height are equal:
R=H
- Therefore, we can write:
u2sin2θg=u2sin2θ2g
3. Simplifying the Equation:
- Cancel u2 and g from both sides (assuming u≠0 and g≠0):
sin2θ=12sin2θ
- Using the identity sin2θ=2sinθcosθ, we can rewrite the equation:
2sinθcosθ=12sin2θ
4. Rearranging the Equation:
- Multiply both sides by 2 to eliminate the fraction:
4sinθcosθ=sin2θ
- Rearranging gives:
sin2θ−4sinθcosθ=0
- Factoring out sinθ:
sinθ(sinθ−4cosθ)=0
5. Finding tanθ:
- Since sinθ≠0 for a projectile, we have:
sinθ=4cosθ
- Dividing both sides by cosθ gives:
tanθ=4
6. Calculating Maximum Height:
- We can find sin2θ using tanθ:
tanθ=sinθcosθ⟹sinθ=4cosθ
- Using sin2θ+cos2θ=1:
(4cosθ)2+cos2θ=1⟹16cos2θ+cos2θ=1
17cos2θ=1⟹cos2θ=117
- Thus, sin2θ=42cos2θ=16⋅117=1617.
7. Substituting to Find Maximum Height:
- Now substituting sin2θ into the height formula:
H=u2sin2θ2g=u2⋅16172g=8u217g
Final Answer:
The maximum vertical height H is:
H=8u217g
- The formula for the horizontal range R of a projectile is given by:
R=u2sin2θg
- The formula for the maximum height H of a projectile is given by:
H=u2sin2θ2g
- According to the problem, the horizontal range and maximum height are equal:
R=H
- Therefore, we can write:
u2sin2θg=u2sin2θ2g
- Cancel u2 and g from both sides (assuming u≠0 and g≠0):
sin2θ=12sin2θ
- Using the identity sin2θ=2sinθcosθ, we can rewrite the equation:
2sinθcosθ=12sin2θ
- Multiply both sides by 2 to eliminate the fraction:
4sinθcosθ=sin2θ
- Rearranging gives:
sin2θ−4sinθcosθ=0
- Factoring out sinθ:
sinθ(sinθ−4cosθ)=0
- Since sinθ≠0 for a projectile, we have:
sinθ=4cosθ
- Dividing both sides by cosθ gives:
tanθ=4
- We can find sin2θ using tanθ:
tanθ=sinθcosθ⟹sinθ=4cosθ
- Using sin2θ+cos2θ=1:
(4cosθ)2+cos2θ=1⟹16cos2θ+cos2θ=1
17cos2θ=1⟹cos2θ=117
- Thus, sin2θ=42cos2θ=16⋅117=1617.
- Now substituting sin2θ into the height formula:
H=u2sin2θ2g=u2⋅16172g=8u217g
The maximum vertical height H is:
H=8u217g
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A body is projected with velocity u such that in horizontal range and maximum vertical heights are samek.The maximum height is
View Solution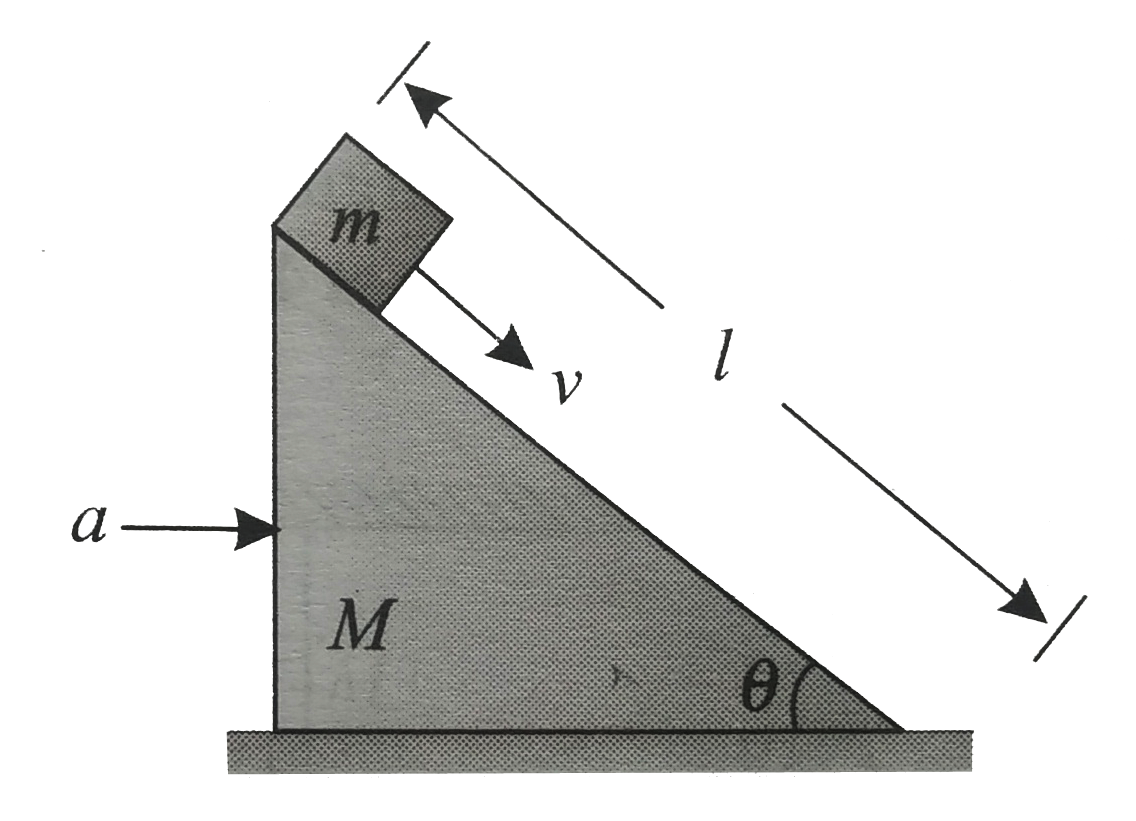
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View SolutionA body is projected with kinetic energy E such that its range is maximum. Its potential energy at the maximum height is
View SolutionFrom a point on the ground a particle is projected with initial velocity u, such that its horizontal range is maximum. The magnitude of average velocity during its ascent is
View SolutionA body is projected vertically up with u. Its velocity at half its maximum height is
View SolutionFind the angle of projection of a projectile for which the horizontal range and maximum height are equal.
View SolutionFind the angle of projection of a projectile for which the horizontal range and maximum height are equal.
View SolutionA stone projected with a velocity u at an angle (theta )with the horizontal reaches maximum heights H1. When it is projected with velocity u at an angle (π2−θ) with the horizontal, it reaches maximum height H2. The relations between the horizontal range R of the projectile, H1andH2, is
View SolutionAn object is projected at an angle of 45∘ with the horizontal. The horizontal range and the maximum height reached will be in the ratio.
View Solution

