A cannon on a level plane is aimed at an angle above the horizontal and a shell is fired with a muzzle velocity towards a vertical cliff a distance R away. Then the height from the bottom at which the shell strikes the side walls of the cliff is
(a)
(b)
(c)
(d)
The correct Answer is:C
To solve the problem of determining the height at which the shell strikes the vertical cliff, we can break down the motion of the shell into horizontal and vertical components. Here’s a step-by-step solution:
Step 1: Identify the initial conditions
- The cannon fires a shell with an initial velocity v0 at an angle α above the horizontal.
- The horizontal distance to the cliff is R.
Step 2: Resolve the initial velocity into components
- The horizontal component of the initial velocity v0x is given by:
v0x=v0cosα
- The vertical component of the initial velocity v0y is given by:
v0y=v0sinα
Step 3: Determine the time of flight to reach the cliff
- The time t taken to reach the cliff can be found using the horizontal motion equation:
R=v0x⋅t⟹t=Rv0cosα
Step 4: Calculate the vertical position when the shell reaches the cliff
- The vertical position y of the shell at time t can be calculated using the vertical motion equation:
y=v0y⋅t−12gt2
- Substituting v0y and t:
y=(v0sinα)(Rv0cosα)−12g(Rv0cosα)2
Step 5: Simplify the equation
- The first term simplifies to:
y=Rtanα
- The second term simplifies to:
12g(R2v20cos2α)
- Thus, the equation for y becomes:
y=Rtanα−gR22v20cos2α
Final Result
- The height h at which the shell strikes the cliff is:
h=Rtanα−gR22v20cos2α
- The cannon fires a shell with an initial velocity v0 at an angle α above the horizontal.
- The horizontal distance to the cliff is R.
- The horizontal component of the initial velocity v0x is given by:
v0x=v0cosα
- The vertical component of the initial velocity v0y is given by:
v0y=v0sinα
- The time t taken to reach the cliff can be found using the horizontal motion equation:
R=v0x⋅t⟹t=Rv0cosα
- The vertical position y of the shell at time t can be calculated using the vertical motion equation:
y=v0y⋅t−12gt2
- Substituting v0y and t:
y=(v0sinα)(Rv0cosα)−12g(Rv0cosα)2
- The first term simplifies to:
y=Rtanα
- The second term simplifies to:
12g(R2v20cos2α)
- Thus, the equation for y becomes:
y=Rtanα−gR22v20cos2α
- The height h at which the shell strikes the cliff is:
h=Rtanα−gR22v20cos2α
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
View SolutionThe surface of a hill is inclined at an angle α to the horizontal .A stone is thrown from the summit of the hill at an angle β to the vertical with velocity v0.How far from the summit will the stone strike the ground ?
View SolutionA projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
View SolutionA ladder rests against a vertical wall at angle α to the horizontal . If is foot is pulled away from the wall through a distance 'a' so that it slides a distance 'b' down the wall making the angle β with the horizontal , then a =
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View SolutionTwo identical shells are fired from a point on the ground with same muzzle velocity at angle of elevation α=45∘ and β=tan−13 towards top of a cliff, 20m away from the point of firing. If both the shells reach the top simultaneously, then
height of the cliff is
View SolutionA shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is ∝=30∘ and the angle of the barrel to the horizontal β=60∘. The initial velocity v of the shell is 21ms−1. Then find the distance of point from the gun at which the shell will fall.
View SolutionFour cannon balls, (1),(2),(3),and(4) are fired from level ground. Cannon ball (1) is fired at an angle of 60∘ above the horizontal and follows the path shown in (Fig. 5.9).
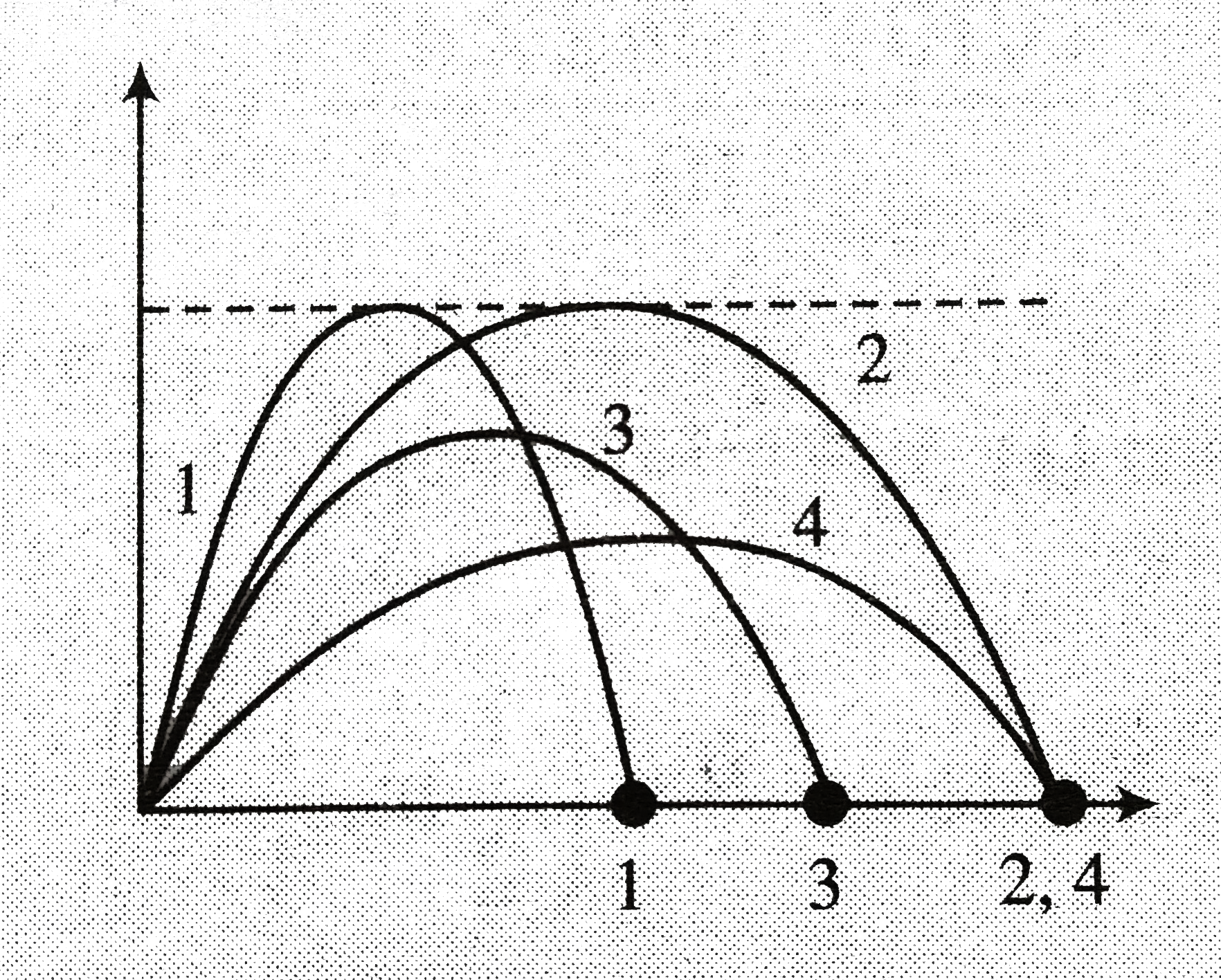 .
.
Cannon balls (2) and (3) are fired at angle of 45∘ and (4) is fired at an angle of 30∘ above the horozontal. Which cannon ball has the largest initial speed ?
View Solution

