Find the point on the curve $y^{2} = a x$ the tangent at which makes an angle of 45^0 with the x-axis.

Video Solution

Text Solution

Verified by Experts

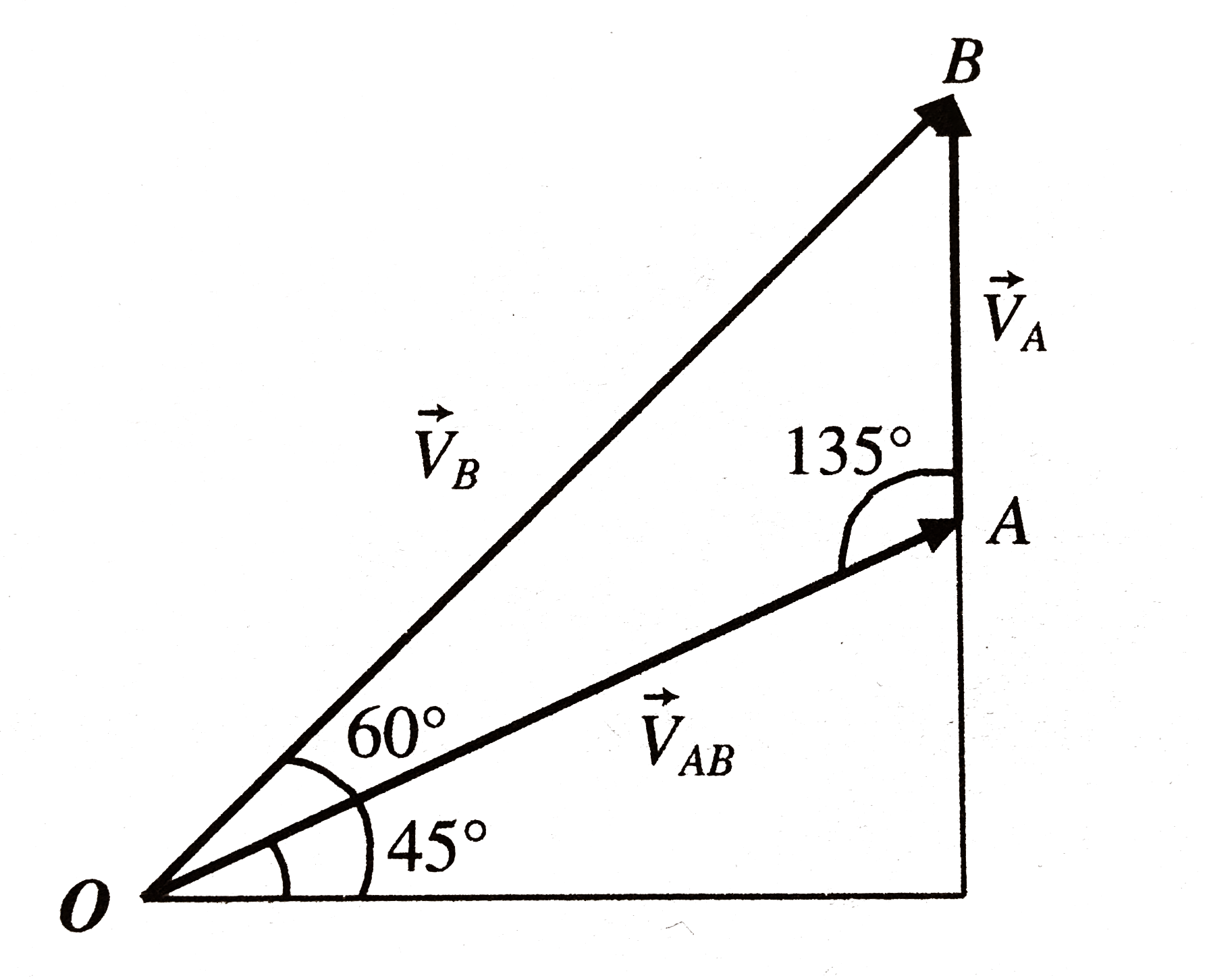
Method 1 : (a) Since the ball hits the trolley, relative to trolley, the velocity of ball should be directed towards the trolley. Hence, in the frame of trolley, the ball will appear to be moving towards $O A$ , or in the frame of trolley, ball's velocity will make an angle of $45^{\circ}$ .
(b) $ϕ = \frac{4 θ}{3} = \frac{4 \times 45^{\circ}}{3} = 60^{\circ}$
Using sine rule $\frac{V_{B}}{{sin 135}^{\circ}} = \frac{V_{A}}{{sin 15}^{\circ}}$
$\Rightarrow V_{B} = 2 m s^{- 1}$
Method 2 : (a) Let $A$ stands for trolley and $B$ for ball.
Relative velocity of $B$ will respect to $A ({\to v}_{B A})$ should be along $O A$ for the ball to hit the trolley.
Hence, ${\to v}_{B A}$ will make an angle of $45^{\circ}$ with positive x - axis.
(b) $tan θ = \frac{v_{B A y}}{v_{B A x}} = {tan 45}^{\circ} or v_{B A y} = v_{B A x}$ ...(i)
Further $v_{B A y} = v_{B y} - v_{A y} or v_{B A x} = v_{B x} - 0$ ...(ii)
$v_{B y} - (\sqrt{3 - 1})$
$tan θ = \frac{v_{B y}}{v_{B x}} or v_{B y} = v_{B x} tan ϕ$
From (i),(ii),(iii), and (iv), we get
$v_{B x} = \frac{(\sqrt{3 - 1})}{tan ϕ - 1} and v_{B y} = \frac{(\sqrt{3 - 1})}{tan θ - 1} tan ϕ$
$ϕ = \frac{4 θ}{3} = \frac{4}{3} (45^{\circ})$
Speed of ball w.r.t. surface,
$v_{B} = \sqrt{v_{B x}^{2} + v_{B y}^{2}} = \frac{\sqrt{3 - 1}}{tan ϕ - 1} sec ϕ$
Substituting $ϕ = 60^{\circ}$ , we get $v_{B} = 2 m s^{- 1}$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The point on the curve $y^{2} = x$ , where tangent make an angle of $\frac{π}{4}$ with the x-axis, is
A $(\frac{1}{2}, \frac{1}{4})$
B $(\frac{1}{4}, \frac{1}{2})$
C(4,2)
D(1,1)

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Solved Examples

Home
Ask Doubt
Profile