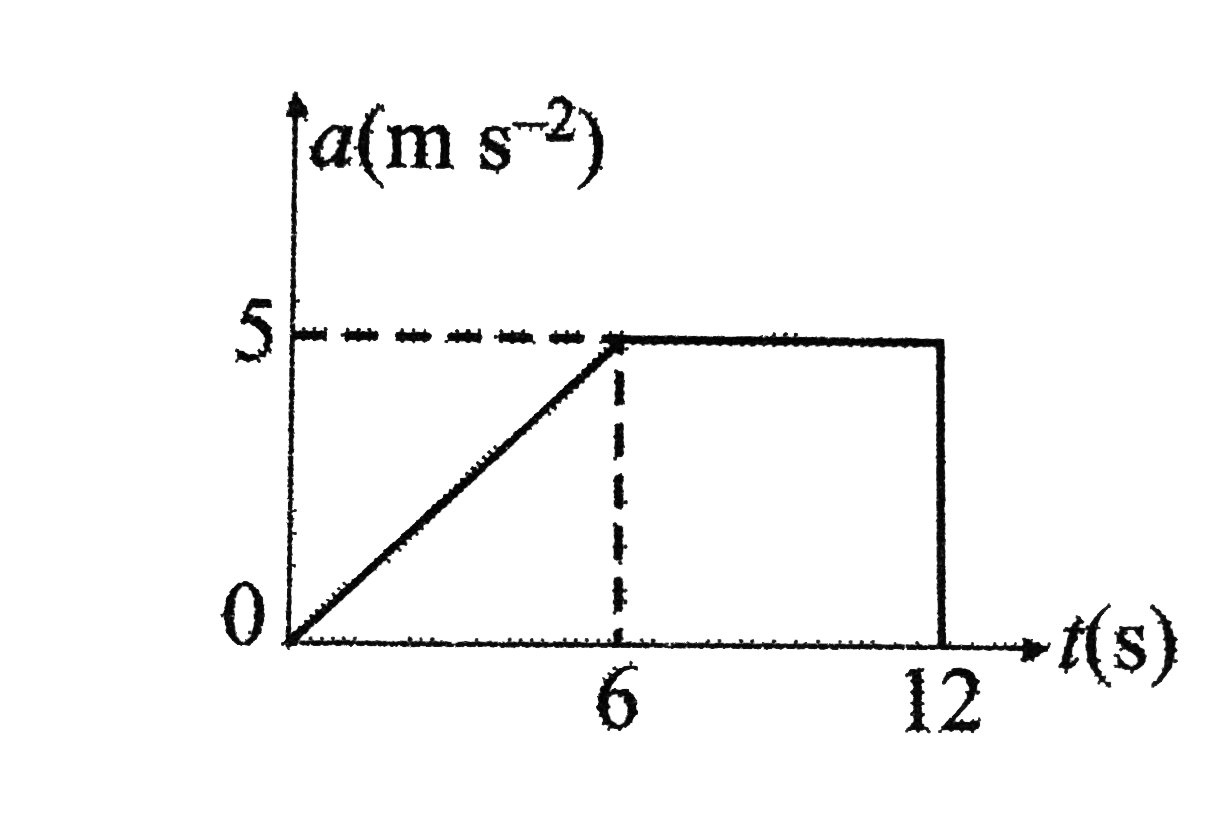
An experiment on the take off performance of an aeroplane shows that the acceleration vaies as shown in (figure) and that it takes 12s to take off from a rest position.
a. Write the acceleration vs. time, velocity vs. time and position vs. time relations for complete journey.
b. Plot velocity vs. time relation for the motion.
c. Find the distance along the run way covered by the aeroplane.
For time t=0 to 6s
We can write equation for this motion, it is y=mx type line where m is the slope of the line.
Here, a=(5−0)(6−0)⋅t⇒a=56t(ms−2) …(i)
(For0≤t<6s)
From 6s to 12s acceleration is constant, we can write equation for this motion, it is y=constant.
Hence a=5(ms−2) (For6≤t<12s)
For time t=0 to 6s
From Eq. (i) a=dvdt=56t⇒dv=56tdt
Integrating both sides, we get v∫0dv=56t∫0tdt
[v]v0=56[t22]t0 or (v−0)=512(t2−0) or v=512t2
Here velocity at t=6s is vt=6s=512×62=15ms−1
For time t=0 to 6s
The acceleration is constant.
a=5(ms−2) or dvdt=5 or dv=5dt
Integrating both sides, v∫15dv=t∫65⋅dt
[v]v15=5[t]t6
v−15=5[t−6]
⇒v=5t−15
Velocity-time relation will be a straight line of type y=mx+c.
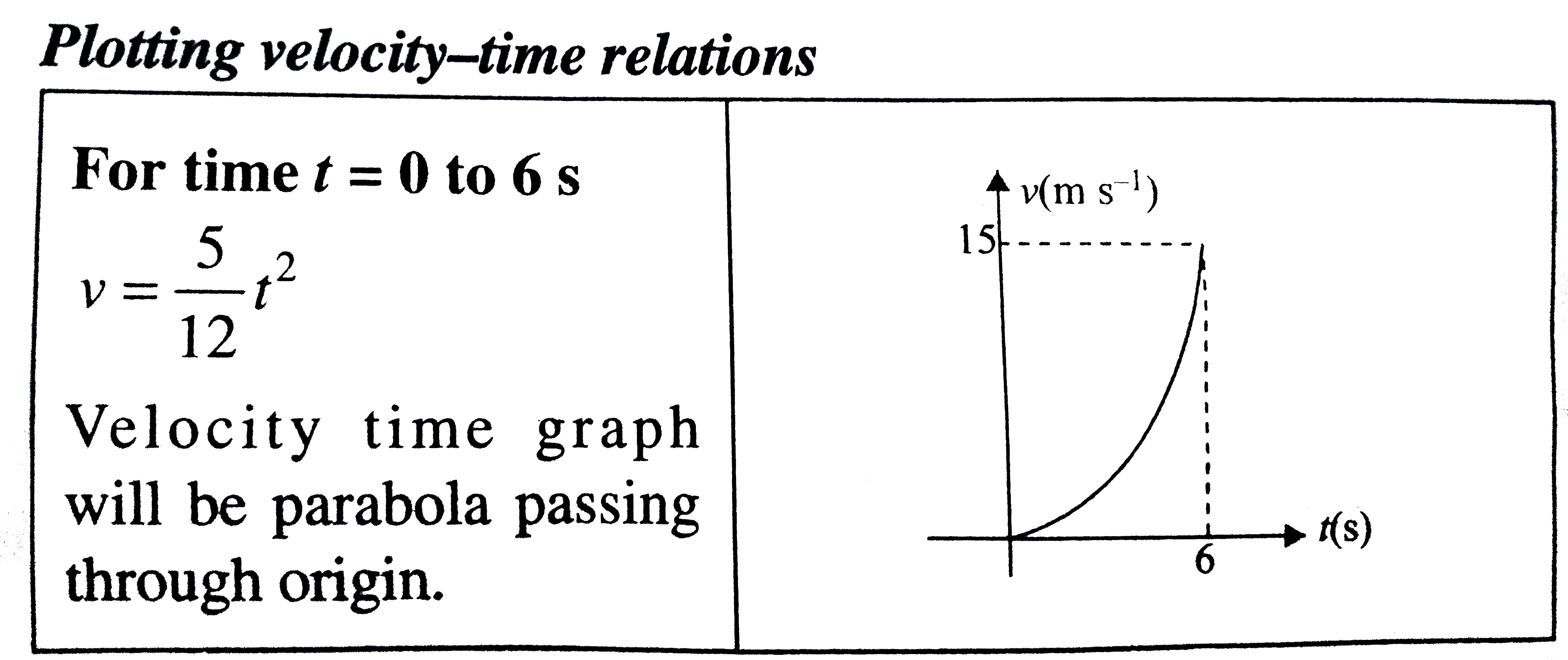
Plotting velocity-time relations
For time t=0 to 6s
v=512t2
Velocity time graph will be parabola passing through origin.
Position time relations
For time t=0 to 6s
As we know v=dxdt=512t2
Hence, 512t2=dxdt⇒dx=512∫t2dt
Integrating both sides, x∫0dx=512t∫0t2dt
(x−0)=512[t33]t0⇒x=536t3
Position or the distance travelled from 0 to 6s
x(t=6sec)=536×(6)3=30m
For time t=6s to 12s
v=5t−15⇒dxdt=5t−5
or dx=(5t−15)dt
Integrating both sides
x∫30dx=t∫6(5t−15)dt
[x]x30=5t∫6tdt−15t∫6dt
(x−30)=5[t22]t6−15[t]t6
x−30=52[t2−62]−15[t−6]
x=52t2−15t+30
At t=12s,
x(t=12s)=52(12)2−15×12+30=210m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.12videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.23videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer4videos
ARCHIVES 2 VOLUME 6
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Position-time graph for motion with zero acceleration is
A B
B C
C D
D
Position - time graph for motion with negative acceleration is
View SolutionThe acceleration of a cart started at t=0 varies with time as shown in figure. Find the distance travelled in 30 seconds and draw the position time graph.
 View Solution
View SolutionThe velocity of a car as a function of time is shown in Fig. Find the distance travelled by the car in 8s and its acceleration.
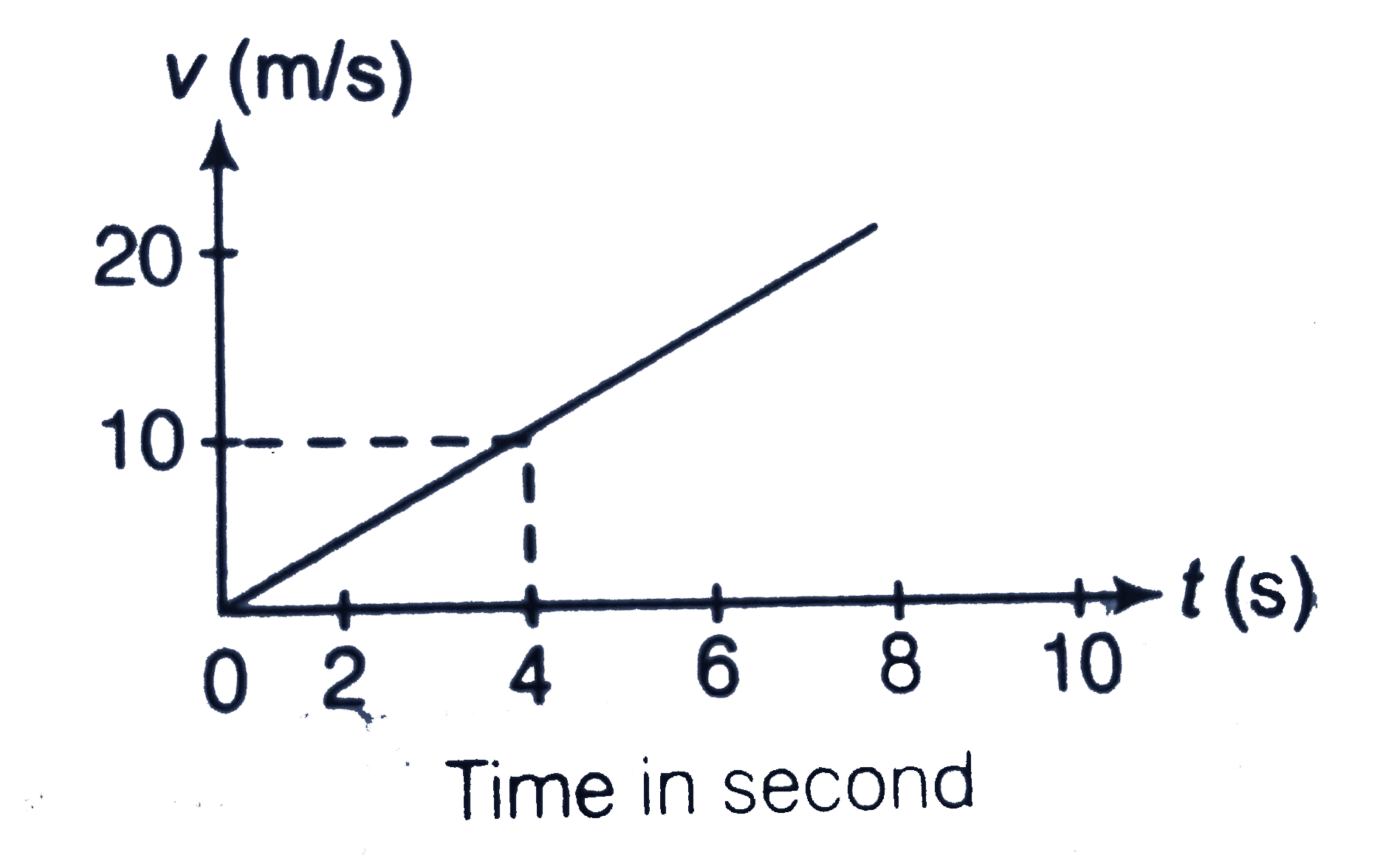 View Solution
View SolutionThe acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
View SolutionFor the motion with uniform velocity, how is the distance travelled related to the time ?
View SolutionThe dependence of the acceleration of a body with time is shown in Figure. At t=0, the velocity of the body is −3m/s and position is x=0m.
 View Solution
View SolutionFor a zero order reaction, the plot of concentration, vs time is linear with
View Solution

