For the motion with uniform velocity, how is the distance travelled related to the time ?
To solve the question of how the distance traveled is related to time for motion with uniform velocity, we can follow these steps:
1. Understanding Uniform Velocity:
- Uniform velocity means that an object travels equal distances in equal intervals of time, regardless of how small those intervals are.
2. Using the Formula:
- The fundamental formula that relates distance (d), velocity (v), and time (t) is:
d=v×t
- Here, d is the distance traveled, v is the uniform velocity, and t is the time taken.
3. Direct Proportionality:
- From the equation d=v×t, we can see that if the velocity v is constant, then the distance d is directly proportional to time t. This can be expressed as:
d∝t
- This means that if time increases, distance also increases proportionally, provided the velocity remains constant.
4. Graphical Representation:
- When we plot distance (d) on the y-axis and time (t) on the x-axis, the graph will be a straight line that passes through the origin. The equation of this line can be represented as:
d=k×t
- Here, k is the constant of proportionality, which in this case is the uniform velocity v.
5. Slope of the Graph:
- The slope of the line in the distance-time graph represents the velocity. Mathematically, the slope (m) can be defined as:
m=dt=v
- This confirms that the slope of the distance-time graph gives the uniform velocity of the object.
Conclusion:
- In conclusion, for motion with uniform velocity, the distance traveled is directly proportional to the time taken, and this relationship can be represented graphically as a straight line with a slope equal to the uniform velocity.
---
- Uniform velocity means that an object travels equal distances in equal intervals of time, regardless of how small those intervals are.
- The fundamental formula that relates distance (d), velocity (v), and time (t) is:
d=v×t
- Here, d is the distance traveled, v is the uniform velocity, and t is the time taken.
- From the equation d=v×t, we can see that if the velocity v is constant, then the distance d is directly proportional to time t. This can be expressed as:
d∝t
- This means that if time increases, distance also increases proportionally, provided the velocity remains constant.
- When we plot distance (d) on the y-axis and time (t) on the x-axis, the graph will be a straight line that passes through the origin. The equation of this line can be represented as:
d=k×t
- Here, k is the constant of proportionality, which in this case is the uniform velocity v.
- The slope of the line in the distance-time graph represents the velocity. Mathematically, the slope (m) can be defined as:
m=dt=v
- This confirms that the slope of the distance-time graph gives the uniform velocity of the object.
- In conclusion, for motion with uniform velocity, the distance traveled is directly proportional to the time taken, and this relationship can be represented graphically as a straight line with a slope equal to the uniform velocity.
Topper's Solved these Questions
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (B) ( Multiple choice type :)
Explore 3 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (B) ( Numericals )
Explore 12 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (A) ( Numericals )
Explore 16 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
Explore 1 Video
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise -4(B)Numericals
Explore 5 Videos
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is
AzeroBAC2AD4A
If body having initial velocity zero is moving with uniform acceleration 8m/sec2 the distance travelled by it in fifth second will be
View SolutionFrom the velocity time plot shown in figure find the distance travelled by the particle dureing the first 40 seconds. Also find the average velocity during this period.

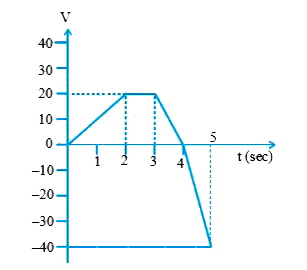
View SolutionIn the following velocity time graph of a body the distance travelled by the body and its displacement during 5 second in meter will be:
View SolutionFrom the velocity-time plot shown in Fig. find the distance travelled by the particle during the first 40s. Also find the average velocity during this period.

View SolutionDraw a velocity-time graph for a body moving with an initial velocity u and uniform acceleration a. Use this graph to find the distance travelled by the body in time t.
View SolutionA person travelling on a straight line moves with a uniform velocity v1 for a distance x and with a uniform velocity v2 for the next equal distance. The average velocity v is given by
View SolutionA steamboat is moving at velocity v0 when steam is shut off. It is given that the retardation at any subsequent time is equal to the magnitude of the velocity at that time. Find the velocity and distance travelled in time t after the steam is shut off.
View Solution

