From point A located on a highway (figure) one has to get by car as soon as possible to point B located in the field at a distance l from the highway. It is known that the car moves in the field η times slower than on the highway. At what distance from point D one must turn off the highway? 
Suppose at x distance from D the car turns off the highway.
Let v be the speed of car on highway, then its speed on field will be v/η.
Time of motion = Time to travel on highway+Time to travel on field
Time to travel on highway, Thighway=AD−xv
Time to travel on field, Tfield=√x2+l2v/η
Here, total time, T=(AD−xv)+√x2+l2v/η ...(i)
If T to be minimum, dTdx=0
dtdx=ddx[AD−xv+ηv(x2+l2)1/2] [AD is constant]
0=−1v+ηv×12(x2+l2)−1/2×2x
η2x2=x2+l2⇒x=1√η2−1
Here we need not to do double derivative test as we know the maximum time for this case is not defined.
Topper's Solved these Questions
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.1
2 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.2
3 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
Similar Questions
A man in a car at location Q on a straight highway is moving with speed v He decides to reach a point P in a field at a distance d from the highway (point M) as shown in th e figure . Speed of the car in the field is half to that on the highway what should be the distacne RM so that the time taken to reach P is minimum ?

View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View Solution
Knowledge Check
A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
Adirected perpendicular to the plane and away from the plane.Bdirected perpendicular to the plane but towards the plane.Cdirected radially away from the point charge.Ddirected radially towards the point charge.The figure shows the path of a car moving around a circular recetrack . How many miles does the car travel in going from point A to Point B?
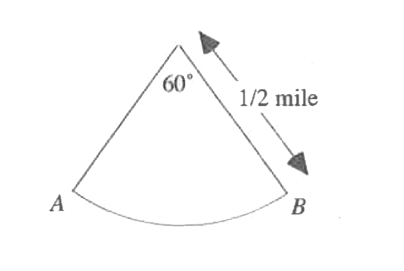 Aπ/6Bπ/3CπD30
Aπ/6Bπ/3CπD30
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA few spherical equipotential surfaces are shown in the figure. The electric field at any point, at a distance x from the centre, is
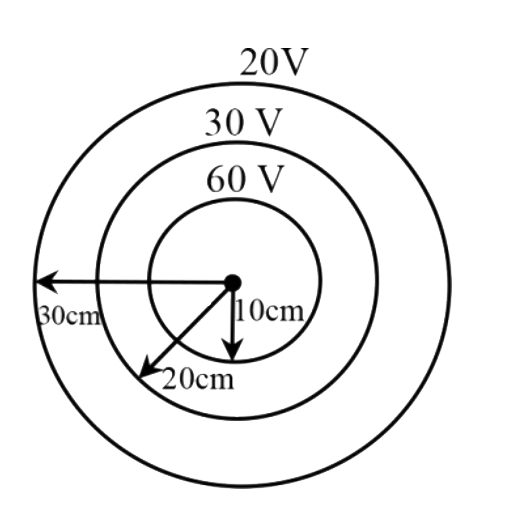
View SolutionThe electric field of an electric dipole at a point on its axis , at a distance d from the centre of the dipole, varies as
View SolutionFour identical charges Q are fixed at the four corners of a square of side a. The electric field at a point P located symmetrically at a distance a/√2 from the center of the square is
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionDerive an expression for the magnetic field at a point on the axis located at a distance x from the centre of a magnetic dipole of length 2l and magnetic moment M.
View Solution
