Which of the following product of e,h,μ,G ( where μ is permeability ) be taken so that the dimensions of the product are same as that of the speed of light ?
he−2μ−1G0
h2eG0μ
h0e2G−1μ
he−2μ0
The correct Answer is:A
To solve the problem of determining which product of e,h,μ,G gives dimensions equivalent to the speed of light c, we will follow these steps:
Step 1: Understand the dimensions of speed of light
The speed of light c has dimensions given by:
(c)=L1T−1
Step 2: Write the relationship
We assume that the speed of light can be expressed in terms of the variables e,h,μ,G as:
c∝eahbμcGd
where a,b,c,d are the powers we need to determine.
Step 3: Write the dimensional formulas
Next, we need the dimensional formulas for each of the quantities:
- Electric charge e: (e)=AT
- Planck's constant h: (h)=ML2T−1
- Permeability μ: (μ)=MLT−2A−2
- Gravitational constant G: (G)=M−1L3T−2
Step 4: Write the dimensions in terms of a,b,c,d
Now, we can express the dimensions of the right-hand side:
(ea)=(AT)a=AaTa
(hb)=(ML2T−1)b=MbL2bT−b
(μc)=(MLT−2A−2)c=McLcT−2cA−2c
(Gd)=(M−1L3T−2)d=M−dL3dT−2d
Step 5: Combine the dimensions
Combining these, we get:
(eahbμcGd)=Mb+c−dL2b+c+3dTa−b−2c−2dAa−2c
Step 6: Set up equations
We equate the dimensions from both sides:
- For M: 0=b+c−d (Equation 1)
- For L: 1=2b+c+3d (Equation 2)
- For T: −1=a−b−2c−2d (Equation 3)
- For A: 0=a−2c (Equation 4)
Step 7: Solve the equations
From Equation 4, we have:
a=2c
Substituting a=2c into Equation 3 gives:
−1=2c−b−2c−2d⟹−1=−b−2d⟹b+2d=1(Equation5)
Now substituting a=2c into Equation 1 gives:
0=b+c−d(Equation1)
Now we have two equations (Equation 1 and Equation 5):
1. b+c−d=0
2. b+2d=1
From Equation 1, we can express c:
c=d−b
Substituting into Equation 5:
b+2d=1⟹b+2(d−b)=1⟹b+2d−2b=1⟹−b+2d=1⟹b=2d−1
Substituting b=2d−1 back into Equation 1:
2d−1+c−d=0⟹c=−d+1
Step 8: Find values of a,b,c,d
Now we can express everything in terms of d:
- b=2d−1
- c=−d+1
- a=2(−d+1)=−2d+2
Step 9: Solve for d
Substituting d=0 gives:
- b=1
- c=1
- a=−2
Final expression
Thus, we find:
c∝e−2h1μ−1G0
This means the correct product is:
c∝he2μ
Final Answer
The correct option is e−2h1μ−1.
The speed of light c has dimensions given by:
(c)=L1T−1
We assume that the speed of light can be expressed in terms of the variables e,h,μ,G as:
c∝eahbμcGd
where a,b,c,d are the powers we need to determine.
Next, we need the dimensional formulas for each of the quantities:
- Electric charge e: (e)=AT
- Planck's constant h: (h)=ML2T−1
- Permeability μ: (μ)=MLT−2A−2
- Gravitational constant G: (G)=M−1L3T−2
Now, we can express the dimensions of the right-hand side:
(ea)=(AT)a=AaTa
(hb)=(ML2T−1)b=MbL2bT−b
(μc)=(MLT−2A−2)c=McLcT−2cA−2c
(Gd)=(M−1L3T−2)d=M−dL3dT−2d
Combining these, we get:
(eahbμcGd)=Mb+c−dL2b+c+3dTa−b−2c−2dAa−2c
We equate the dimensions from both sides:
- For M: 0=b+c−d (Equation 1)
- For L: 1=2b+c+3d (Equation 2)
- For T: −1=a−b−2c−2d (Equation 3)
- For A: 0=a−2c (Equation 4)
From Equation 4, we have:
a=2c
−1=2c−b−2c−2d⟹−1=−b−2d⟹b+2d=1(Equation5)
0=b+c−d(Equation1)
1. b+c−d=0
2. b+2d=1
c=d−b
Substituting into Equation 5:
b+2d=1⟹b+2(d−b)=1⟹b+2d−2b=1⟹−b+2d=1⟹b=2d−1
2d−1+c−d=0⟹c=−d+1
Now we can express everything in terms of d:
- b=2d−1
- c=−d+1
- a=2(−d+1)=−2d+2
Substituting d=0 gives:
- b=1
- c=1
- a=−2
Thus, we find:
c∝e−2h1μ−1G0
This means the correct product is:
c∝he2μ
The correct option is e−2h1μ−1.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Linked Comprehension
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Subjective
31 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
In which of the following reactions product formed is same ?
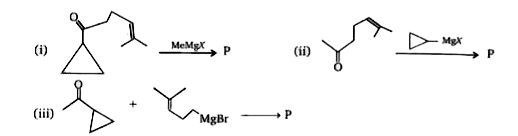 A(i) and (ii)B(ii) and (iii)C(i) and (iii)D(i), (ii) and (iii)
A(i) and (ii)B(ii) and (iii)C(i) and (iii)D(i), (ii) and (iii)Which of the following reactions produce the same product?
A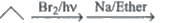 B
B C
C D
D
Which of the following reactions produce the same product?
A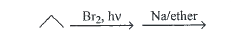 B
B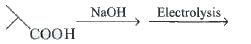 C
C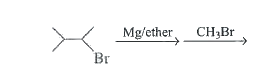 D
D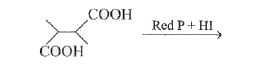
Which of the following is not a product of light reaction of phtosynthesis
View SolutionPhoton is quantum of radiation with energy E =hv where v is frequency and h is Planck's constant. The dimensions of h are the same as that of
View SolutionWhich of the following will give same product on ozonolysis
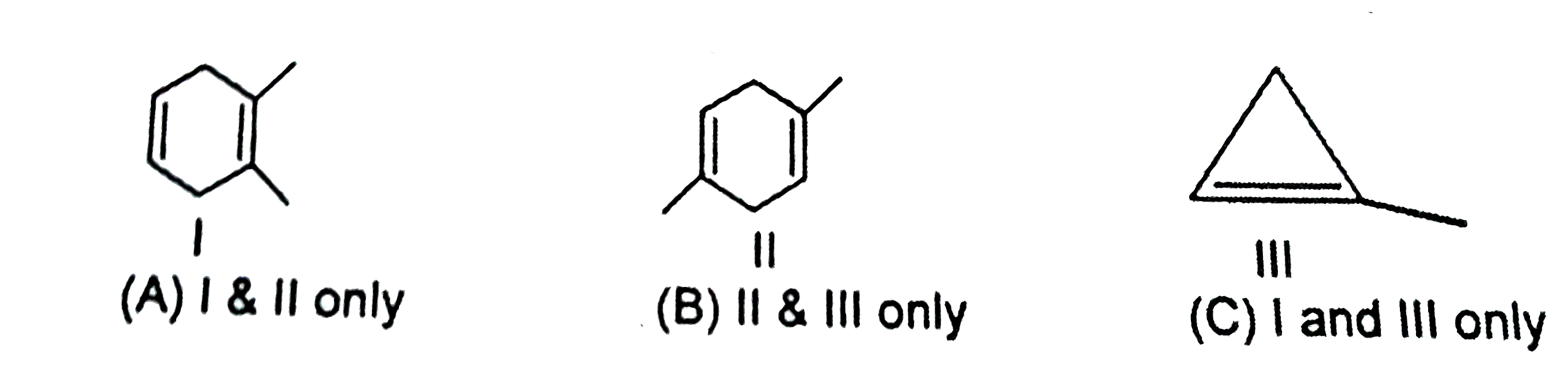
View SolutionWhich of the following is not correct about relative magnetic permeability (μr)?
View SolutionWhich of the following reactions would produce same product?
View Solution
