Given that Y=asinωt+bt+ct2cosωt. The unit of abc is same as that of
y
y/t
(y/t)2
(y/t)3
The correct Answer is:D
To solve the problem, we need to analyze the given expression for Y and determine the relationship between the units of a, b, and c with respect to Y.
Step 1: Identify the expression for Y
The expression given is:
Y=asin(ωt)+bt+ct2cos(ωt)
Step 2: Determine the dimensions of Y
Since Y is a function of time, we can assume that it has dimensions of length (L), which is a common assumption in physics unless stated otherwise. Therefore:
(Y)=L
Step 3: Analyze the first term asin(ωt)
The term sin(ωt) is dimensionless because trigonometric functions do not have dimensions. Thus, the dimension of a must be the same as that of Y:
(a)=(Y)=L
Step 4: Analyze the second term bt
In this term, t has dimensions of time (T). Therefore, for the term bt to have dimensions of length (L), the dimension of b must be:
(b)=(Y)(t)=LT
Step 5: Analyze the third term ct2cos(ωt)
Similar to the first term, cos(ωt) is also dimensionless. Therefore, for the term ct2 to have dimensions of length (L), we have:
(ct2)=L⟹(c)(t2)=L
Since t2 has dimensions of T2, we can write:
(c)(T2)=L⟹(c)=LT2
Step 6: Calculate the product abc
Now, we can find the product abc:
(abc)=(a)(b)(c)=(L)(LT)(LT2)
Calculating this gives:
(abc)=L⋅LT⋅LT2=L3T3
Conclusion
The units of abc are the same as L3T3.
The expression given is:
Y=asin(ωt)+bt+ct2cos(ωt)
Since Y is a function of time, we can assume that it has dimensions of length (L), which is a common assumption in physics unless stated otherwise. Therefore:
(Y)=L
The term sin(ωt) is dimensionless because trigonometric functions do not have dimensions. Thus, the dimension of a must be the same as that of Y:
(a)=(Y)=L
In this term, t has dimensions of time (T). Therefore, for the term bt to have dimensions of length (L), the dimension of b must be:
(b)=(Y)(t)=LT
Similar to the first term, cos(ωt) is also dimensionless. Therefore, for the term ct2 to have dimensions of length (L), we have:
(ct2)=L⟹(c)(t2)=L
Since t2 has dimensions of T2, we can write:
(c)(T2)=L⟹(c)=LT2
Now, we can find the product abc:
(abc)=(a)(b)(c)=(L)(LT)(LT2)
Calculating this gives:
(abc)=L⋅LT⋅LT2=L3T3
The units of abc are the same as L3T3.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Linked Comprehension
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Subjective
31 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
The displacement of an elastic wave is given by the function y=3sinωt+4cosωt.
where y is in cm and t is in second. Calculate the resultant amplitude.A3 cmB4 cmC5 cmD7 cm
The displacement of an elastic wave is given by the function y=3sinωt+4cosωt.
where y is in cm and t is in second. Calculate the resultant amplitude.
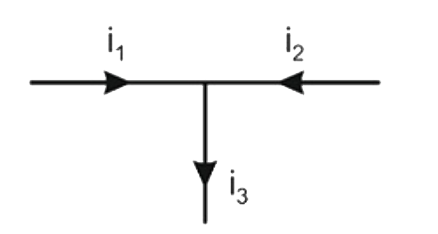
View SolutionIn the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
View SolutionTwo SHM's are represented by y=asin(ωt−kx) and y=bcos(ωt−kx). The phase difference between the two is :
View SolutionThe displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
View SolutionA simple harmonic motion is represented by x(t)=sin2ωt−2cos2ωt. The angular frequency of oscillation is given by
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionTwo simple harmonic motions are given by y1=5sin(ωt−π/3).y2=5(sinωt+√3cosωt). Ratio of their amplitudes is
View Solution
