A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
M g
Mg−Vρ g
Mg+ΠR2hgρ
ρg(V+ΠR2h)
The correct Answer is:d
To solve the problem, we will analyze the forces acting on the cylinder and derive the expression for the force on the bottom of the cylinder by the liquid.
1. Identify the Forces Acting on the Cylinder:
- The force acting on the bottom of the cylinder due to the liquid, denoted as F1.
- The force acting downward on the top of the cylinder due to the liquid, denoted as F2.
- The buoyant force acting upward on the cylinder, which can be expressed as Fb.
2. Apply the Principle of Equilibrium:
- Since the cylinder is in equilibrium (it stays vertical), we can write the equation:
F1−F2=Fb
3. Express the Buoyant Force:
- The buoyant force Fb can be expressed in terms of the volume of liquid displaced:
Fb=V⋅ρ⋅g
where V is the volume of the displaced liquid, ρ is the density of the liquid, and g is the acceleration due to gravity.
4. Calculate the Force F2:
- The force F2 acting downward on the top of the cylinder can be calculated using the pressure at depth h:
F2=P⋅A=(h⋅ρ⋅g)⋅(πR2)
where A=πR2 is the cross-sectional area of the cylinder.
5. Substituting F2 into the Equilibrium Equation:
- Substitute F2 into the equilibrium equation:
F1−(h⋅ρ⋅g⋅πR2)=V⋅ρ⋅g
6. Rearranging to Find F1:
- Rearranging the equation gives:
F1=V⋅ρ⋅g+h⋅ρ⋅g⋅πR2
7. Factor Out Common Terms:
- Factor out ρ⋅g:
F1=ρ⋅g(V+h⋅πR2)
Final Answer:
The force on the bottom of the cylinder by the liquid is:
F1=ρ⋅g(V+h⋅πR2)
- The force acting on the bottom of the cylinder due to the liquid, denoted as F1.
- The force acting downward on the top of the cylinder due to the liquid, denoted as F2.
- The buoyant force acting upward on the cylinder, which can be expressed as Fb.
- Since the cylinder is in equilibrium (it stays vertical), we can write the equation:
F1−F2=Fb
- The buoyant force Fb can be expressed in terms of the volume of liquid displaced:
Fb=V⋅ρ⋅g
where V is the volume of the displaced liquid, ρ is the density of the liquid, and g is the acceleration due to gravity.
- The force F2 acting downward on the top of the cylinder can be calculated using the pressure at depth h:
F2=P⋅A=(h⋅ρ⋅g)⋅(πR2)
where A=πR2 is the cross-sectional area of the cylinder.
- Substitute F2 into the equilibrium equation:
F1−(h⋅ρ⋅g⋅πR2)=V⋅ρ⋅g
- Rearranging the equation gives:
F1=V⋅ρ⋅g+h⋅ρ⋅g⋅πR2
- Factor out ρ⋅g:
F1=ρ⋅g(V+h⋅πR2)
The force on the bottom of the cylinder by the liquid is:
F1=ρ⋅g(V+h⋅πR2)
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION
25 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION (ROTATIONAL MOTION AND MOMENT OF INERTIA )
25 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - FRICTION
22 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
The radius of a cylinder is r and heigth is h. Find its volume.
View SolutionWrite the ratio of total surface area to the surface area of a cylinder of radius r and height h
View SolutionFrom a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :

View SolutionCurved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7m, find its height.
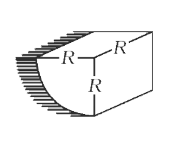
View SolutionA hollow cylinder of radius R and length R is cut into four equal parts from its axis. Each one is called quarter cylinder. If the quarter cylinder is just completely immersed in a liquid of density ρ, find the horizontal thrust acting on the curved surface of the cylinder.
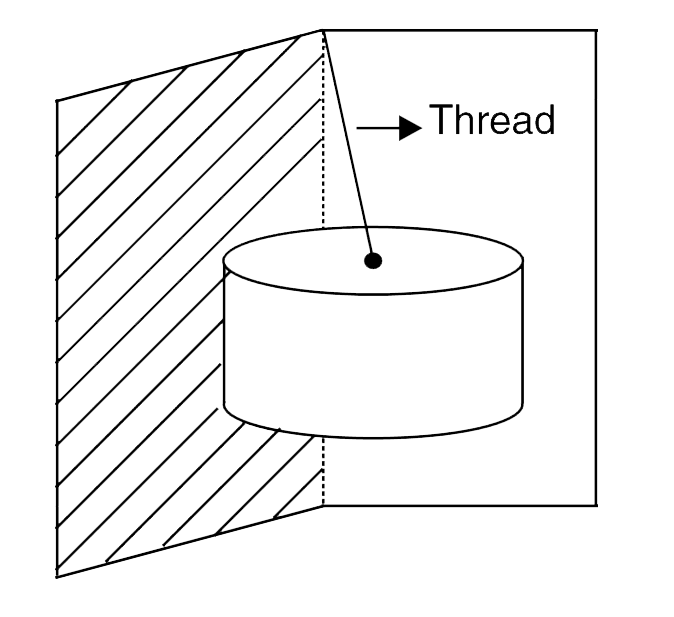
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View SolutionThe ratio between the radius of the base and the height of a cylinder is 2:3., find the total surface area of the cylinder, it its volume is 1617 cm3.
View Solution