An inverted vessel (ball) lying at the bottom of a lake, 47.6 m deep, has 50 c.c. of air trapped in it. The bell is brought to the surface of the lake. The volume of the trapped air will now be (Atmospheric pressure is 70 cm of Hg, density of HG - 13.6 g cm−3)
350 c.c.
300 c.c.
250 c.c.
200 c.c.
The correct Answer is:b
To solve the problem step by step, we will use the principles of fluid mechanics and the ideal gas law.
Step 1: Calculate the Pressure at the Bottom of the Lake (P1)
The pressure at the bottom of the lake can be calculated using the formula:
P1=P0+h⋅ρ⋅g
Where:
- P0 = Atmospheric pressure
- h = Depth of the lake = 47.6 m
- ρ = Density of water = 103kg/m3
- g = Acceleration due to gravity = 9.8m/s2
Given that the atmospheric pressure is 70 cm of Hg, we first convert it to Pascals:
P0=70cmHg=0.7m⋅13.6×103Pa
Calculating P0:
P0=0.7×13.6×103=9512Pa
Now, calculate the pressure due to the water column:
Pwater=h⋅ρ⋅g=47.6⋅103⋅9.8
Calculating Pwater:
Pwater=47.6⋅103⋅9.8=466,088Pa
Now, add both pressures to find P1:
P1=9512+466088=475600Pa
Step 2: Use the Ideal Gas Law to Find the Volume at the Surface (V2)
According to Boyle's Law, for a given mass of gas at constant temperature:
P1V1=P2V2
Where:
- V1=50cm3=50×10−6m3
- P2 is the atmospheric pressure at the surface, which is P0=9512Pa
Rearranging the equation to find V2:
V2=P1V1P2
Substituting the values:
V2=475600⋅50×10−69512
Calculating V2:
V2=23780×10−69512≈2.49×10−3m3
Converting V2 to cm³:
V2=2.49×10−3m3=2490cm3
Final Answer
The volume of the trapped air when the vessel is brought to the surface of the lake is approximately 2490 cm³.
P1=P0+h⋅ρ⋅g
- P0 = Atmospheric pressure
- h = Depth of the lake = 47.6 m
- ρ = Density of water = 103kg/m3
- g = Acceleration due to gravity = 9.8m/s2
P0=70cmHg=0.7m⋅13.6×103Pa
P0=0.7×13.6×103=9512Pa
Pwater=h⋅ρ⋅g=47.6⋅103⋅9.8
Pwater=47.6⋅103⋅9.8=466,088Pa
P1=9512+466088=475600Pa
P1V1=P2V2
- V1=50cm3=50×10−6m3
- P2 is the atmospheric pressure at the surface, which is P0=9512Pa
V2=P1V1P2
V2=475600⋅50×10−69512
V2=23780×10−69512≈2.49×10−3m3
V2=2.49×10−3m3=2490cm3
The volume of the trapped air when the vessel is brought to the surface of the lake is approximately 2490 cm³.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:UNIFORM CIRCULAR MOTION
Explore 25 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:UNIFORM CIRCULAR MOTION (ROTATIONAL MOTION AND MOMENT OF INERTIA )
Explore 25 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:FRICTION
Explore 22 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
As an air bubble rises from the bottom of a lake to the surface, its volume is doubled. Find the depth of the lake. Take atmospheric pressure = 76 cm of Hg.
View SolutionCalculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6g cm−3
View SolutionAn air bubble rises from the bottom of a lake of depth 10.34m to its surface. Compare the pressure on bubble at the bottom to that on surface. (Atmospheric pressure =0.76mofHg, density of Hg=13.6×103Kgm−3 and density of water =103kgm−3).
View SolutionAn air bubble starts rising from the bottom of a lake. Its diameter is 3.6mm at the bottom and 4mm at the surface. The depth of the lake is 250cm and the temperature at the surface is 40∘C. What is the temperature at the bottom of the lake? Given atmospheric pressure = 76cmofHgandg=980cm/s2.
View SolutionCalculate the root mean square velocity of nitrogen at 27∘C and 70cm pressure. The density of Hg is 13.6gcm−3.
View SolutionA capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
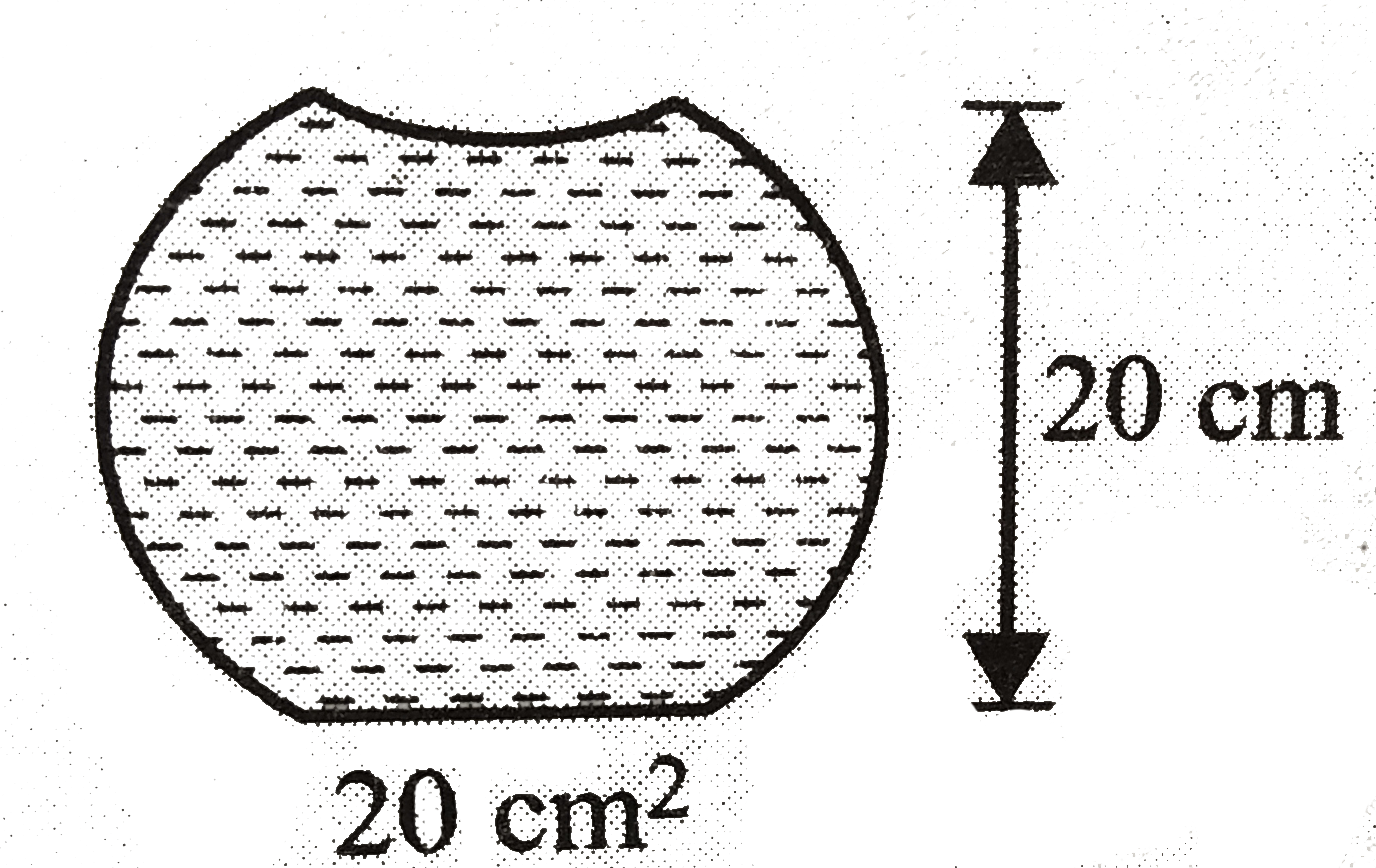
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionAn iron ball has an air space in it, the ball weights ong kg in air and O-6 kg in water. Find the volume of the air space. Density of iron is7200kgm−3.
View SolutionA narrow capillary tube is dipped 10cm below water surface and a liquid bubble of radius 2mm formed at the lower end by blowing air through the tube.
a. Calculate the excess pressure due to surface tension.
b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water?
The surface tension of water at temperature of the experiment is 7.30×10−2N/m. 1 atmospheric pressure =105Pa, density of water =1000kg/m3
View SolutionAn air bubble rises the bottom of a lake to the top and increases thereby its volume 15 times . If the atmospheric pressure is 75 cm of hg and density of lake water is 1.02×103kg/m3 then find the depth of lake ( Neglect surface tension).
View Solution