A pendulum bob is suspended inside a lift moving upward with constant velocity. If mass of the bob is 50 g then its weight inside the compartment is
zero
0.1 N
0.5 N
0.05 N
The correct Answer is:d
To solve the problem of finding the weight of a pendulum bob suspended inside a lift moving upward with constant velocity, follow these steps:
Step 1: Understand the situation
The pendulum bob is suspended in a lift that is moving upward with a constant velocity. Since the lift is moving with constant velocity, the acceleration of the lift is zero.
Step 2: Identify the forces acting on the bob
In this scenario, the forces acting on the bob are:
- The gravitational force (weight) acting downwards, which is given by W=mg.
- The tension T in the string acting upwards.
Step 3: Calculate the mass of the bob
The mass of the bob is given as 50 g. To convert this into kilograms (since the standard unit of mass in physics is kg):
Mass=50g=501000kg=0.05kg
Step 4: Calculate the weight of the bob
The weight of the bob can be calculated using the formula:
W=mg
where g (acceleration due to gravity) is approximately 10m/s2. Substituting the values:
W=0.05kg×10m/s2=0.5N
Step 5: Conclusion
Since the lift is moving with constant velocity, the tension in the string is equal to the weight of the bob. Therefore, the weight of the pendulum bob inside the compartment is:
Weight=0.5N
Final Answer
The weight of the pendulum bob inside the lift is 0.5 N.
---
The pendulum bob is suspended in a lift that is moving upward with a constant velocity. Since the lift is moving with constant velocity, the acceleration of the lift is zero.
In this scenario, the forces acting on the bob are:
- The gravitational force (weight) acting downwards, which is given by W=mg.
- The tension T in the string acting upwards.
The mass of the bob is given as 50 g. To convert this into kilograms (since the standard unit of mass in physics is kg):
Mass=50g=501000kg=0.05kg
The weight of the bob can be calculated using the formula:
W=mg
where g (acceleration due to gravity) is approximately 10m/s2. Substituting the values:
W=0.05kg×10m/s2=0.5N
Since the lift is moving with constant velocity, the tension in the string is equal to the weight of the bob. Therefore, the weight of the pendulum bob inside the compartment is:
Weight=0.5N
The weight of the pendulum bob inside the lift is 0.5 N.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( WORK POWER ENERGY )
Explore 35 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:FRICTION
Explore 22 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
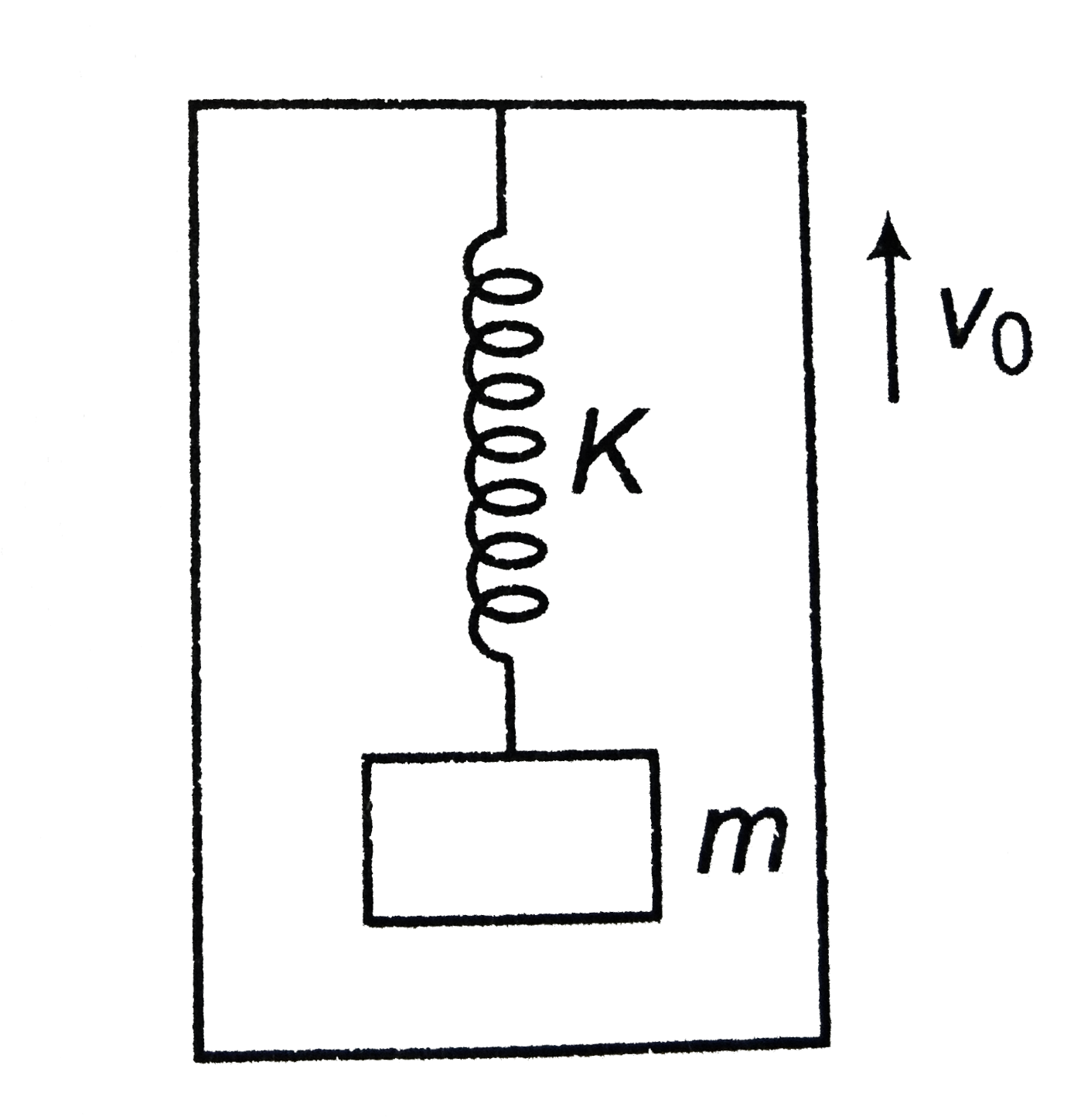
A spring block system is kept inside a lift moving with a constant velocity v0 as shown in figure. Block is in equilibrium and at rest with respect to lift. The lift is suddenly stopped at time t=0. Taking upward direction as the positive direction, write x−t equation of the block.
View SolutionTime period of a spring pendulum when lift moves downward with constant velocity v is T second. When the lift moves upward with constant acceleration=g3 , the time period will be

View SolutionThe apparent weight of man inside a lift moving up with certain acceleration is 900N. When the lift is coming down with the same acceleration apparent weight is found to be 300N. The mass of the man is (g = 10ms−2)
View SolutionA rod is formed by joining two cylinders each having a length l and cross sectional area S. The densities of cylinder are ρ and 2ρ respectively. The rod is now horizontally suspended in a liquid of density 4ρ with help of two string as shown in the figure. The entire setup is kept inside a lift. For the quantities given in List I select the correct value from those mentioned in List II.
List-IList-II(P)Tension in string 1 if the lift is moving upwards with constant velocity(1)118ρSlg(Q)Tension in string 2 if the lift is moving upwards with constant velocity(2)98ρSlg(R)Tension is string 1 if lift is moving downwards with an acceleration of g/2(3)114ρSlg(S)Tension in string 2 if the lift is moving downwards with an acceleration of g/2(4)94ρSlg
Choose the correct option :

View SolutionThe length of a simple pendulum is 16 cm . It is suspended by the roof of a lift which is moving upwards with an accleration of 6.2ms−2 . Find the time period of pendulum.
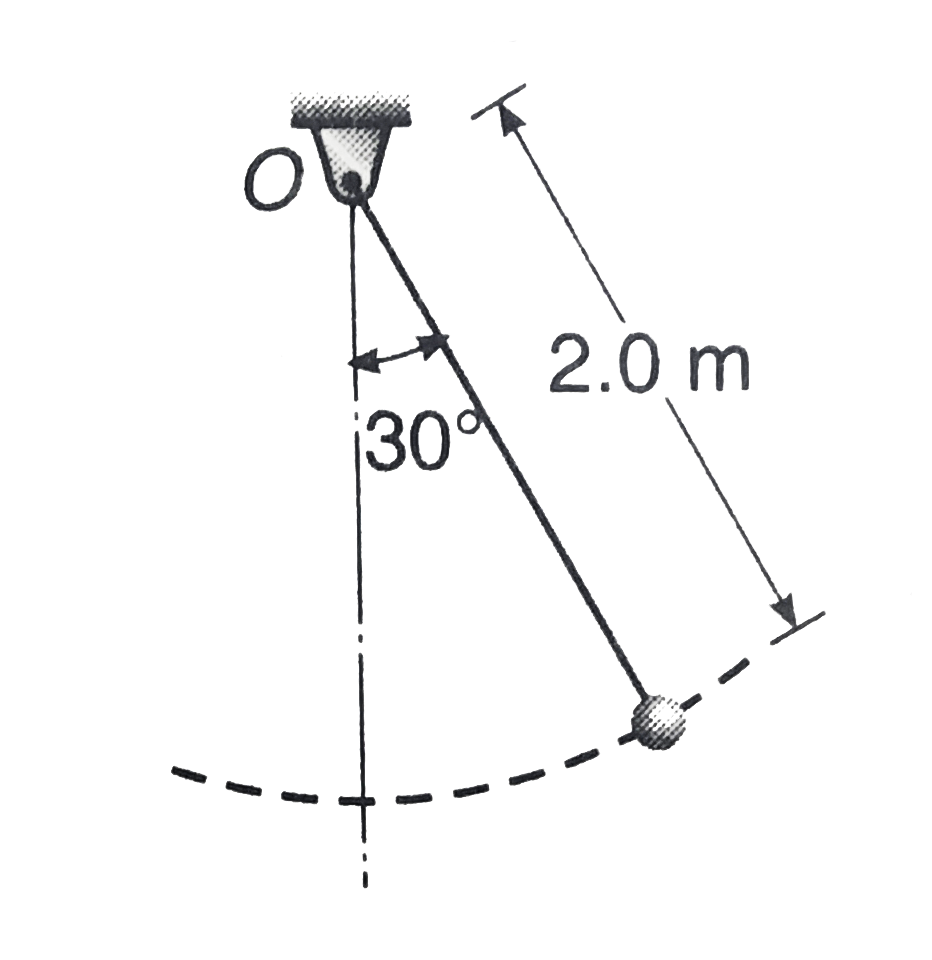
View SolutionThe bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is 2.5 times the weight of the bob for the position shown. Find the velocity and the acceleration of the bob in that position.
View SolutionA plumb bob of mass 1kg is hung from the ceiling of a train compartment.The train moves on an inclined plane with constant velocity. If the angle of inclined is 30∘.Find the angle made by the string with the normal to the ceiling .Also ,Find the tension in the string (g=10m/s2)
View SolutionA plumb bob of mass 1kg is hung from the ceiling of a train compartment.The train moves on an inclined plane with constant velocity. If the angle of inclined is 30∘.Find the angle made by the string with the normal to the ceiling .Also ,Find the tension in the string (g=10m/s2)
View SolutionA pendulum is suspended in a lit and its period of oscillation is T0 when the lift is stationary.
(i) What will be the period T of oscillation of pendulum, if the lift begins to accelerates downwards with an acceleration equal to 3g4 ?
View SolutionA pendulum bob of mass 50 gm is suspended from the ceiling of an elevator. The tension in the string if the elevator goes up with uniform velocity is approximately
View Solution