A ship of mass 3×107 kg initially at rest is pulled by a force of 5×104N through a distance of 3 m. Assume that the resistance due to water is nigligible, the speed of the ship is
1.5 m/s
60 m/s
0.1 m/s
5 m/s
The correct Answer is:c
To solve the problem step by step, we will use the given data and apply the relevant physics concepts.
Given:
- Mass of the ship, m=3×107 kg
- Force applied, F=5×104 N
- Distance moved, s=3 m
- Initial speed, u=0 m/s (since the ship is initially at rest)
Step 1: Calculate the acceleration of the ship
Using Newton's second law of motion, we know that:
F=m⋅a
Where:
- F is the force applied,
- m is the mass of the ship,
- a is the acceleration.
Rearranging the equation to find acceleration:
a=Fm
Substituting the values:
a=5×104N3×107kg=53×10−3m/s2
Step 2: Use the third equation of motion to find the final speed
We will use the third equation of motion:
v2=u2+2as
Where:
- v is the final speed,
- u is the initial speed,
- a is the acceleration,
- s is the distance moved.
Since the initial speed u=0:
v2=0+2as
Substituting the values of a and s:
v2=2(53×10−3)(3)
Calculating further:
v2=2×53×10−3×3=10−2
Step 3: Calculate the final speed
Taking the square root to find v:
v=√10−2=0.1m/s
Final Answer:
The speed of the ship is 0.1m/s.
---
- Mass of the ship, m=3×107 kg
- Force applied, F=5×104 N
- Distance moved, s=3 m
- Initial speed, u=0 m/s (since the ship is initially at rest)
Using Newton's second law of motion, we know that:
F=m⋅a
Where:
- F is the force applied,
- m is the mass of the ship,
- a is the acceleration.
a=Fm
a=5×104N3×107kg=53×10−3m/s2
We will use the third equation of motion:
v2=u2+2as
Where:
- v is the final speed,
- u is the initial speed,
- a is the acceleration,
- s is the distance moved.
v2=0+2as
Substituting the values of a and s:
v2=2(53×10−3)(3)
Calculating further:
v2=2×53×10−3×3=10−2
Taking the square root to find v:
v=√10−2=0.1m/s
The speed of the ship is 0.1m/s.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( WORK POWER ENERGY )
35 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - FRICTION
22 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics (PROJECTILE MOTION)
31 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
A ship of mass 3×107kg initially at rest, is pulled by a force of 5×105N through a distance of 3m. Assuming that the resistance due to water is negligible, the speed of the ship is
View SolutionIf a ship of mass 4×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 4 m, then the speed of the ship will be (resistance due to water is negligible )
View Solution
Knowledge Check
A ship of mass 3×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 3 m. Assuming that the resistance due to water is neglible, what will be the speed of ship ?
A1.5 m/secB60 m/secC0.1 m/secD5m/sec
A ship of mass 3×102kg initially at rest is pulled by a force of 5×104 N through a distance of 3m. Neglecting frcition, the speed of the ship at this moment is:
View SolutionTwo ropes are puling a large ship at rest of mass 1×106kg into harbour. Rope A exerts a force of 40,000N and rope B exerts a force of 30,000N. Also the value of sin inverse θ is 45

If the acceleration of the ship is 0.03ms−2, the magnitude of the resistive forces on the ship is
View SolutionA body of mass 5×103kg moving with speed 2 m/s collides with a body of mass 15×103kg inelastically & sticks to it. Then loss in K.E. of the system will be :
View SolutionA planet has a mass of 2.4×1026 kg with a diameter of 3×108 m. What will be the acceleration due to gravity on that planet ?
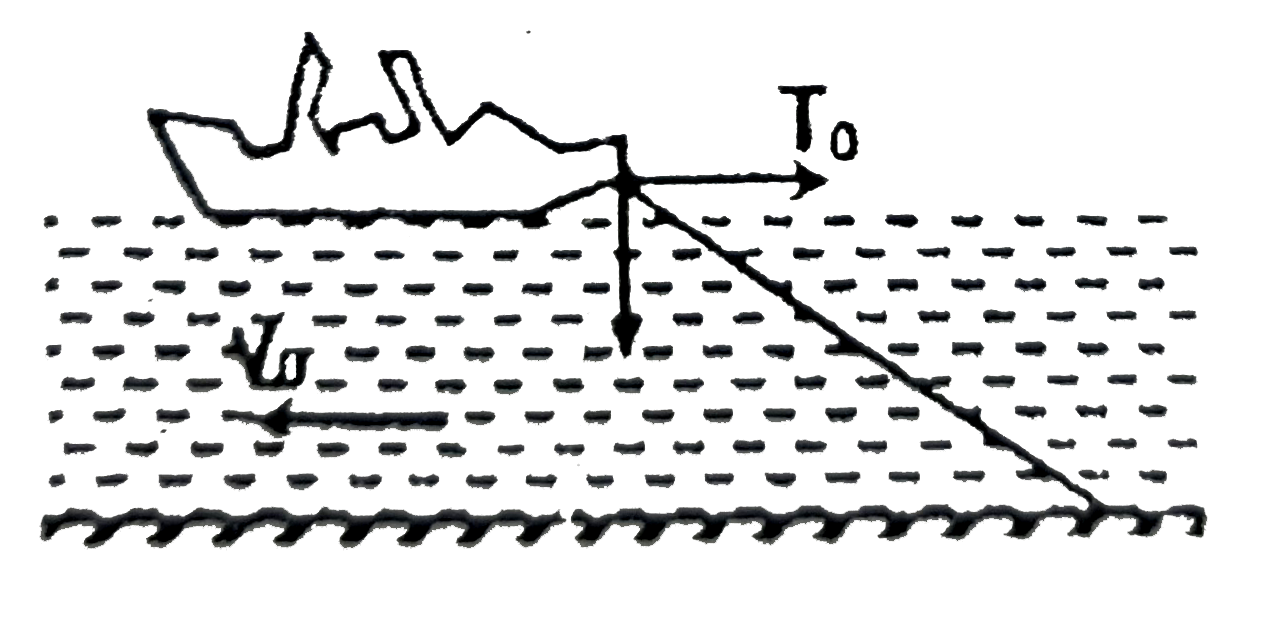
View SolutionA ship of total mass m is anchored in the middle of a river and water is flowing with a constant velocity v0. The horizontal component of the force exerted on the ship by the anchor chain is T0. If the anchor chain suddenly breaks, determine the time required for the ship to attain a velocity equal to 0.5v0. Assume that the fricitional resistance of the water is proportional to the velocity of the ship relative to the water.
View SolutionA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.

View SolutionAn engine of mass5×104 kg pulls a coach of mass 4×104kg. Suppose that there is a resistance of 1 N per 100 kg acting on both coach and engine, and that the driving force is 4500N. The acceleration of the engine and the coupling will respectively be
View Solution
