A particle moves along the circumference of a circle of radius r when its completes one rotation.
Distance travelled is zero and displacement is 2πr
distance and displacement are zero
distance is 2πr but displacement is zero
distance and displacement are 2πr each
The correct Answer is:c
To solve the problem, we need to understand the concepts of distance and displacement in the context of a particle moving along the circumference of a circle.
1. Understanding the Motion:
- A particle moves along the circumference of a circle with radius r.
- It completes one full rotation around the circle.
2. Calculating Distance:
- The distance traveled by the particle is the total length of the path it covers.
- The length of the circumference of a circle is given by the formula:
Distance=2πr
- Since the particle completes one full rotation, the distance traveled is 2πr.
3. Calculating Displacement:
- Displacement is defined as the shortest distance from the initial position to the final position.
- In this case, the particle starts at a point (let's say point A) and after one complete rotation, it returns to the same point (point A).
- Therefore, the initial and final positions are the same, which means:
Displacement=0
4. Final Result:
- The distance traveled by the particle is 2πr.
- The displacement of the particle is 0.
Thus, the correct answer is:
- Distance = 2πr
- Displacement = 0
- A particle moves along the circumference of a circle with radius r.
- It completes one full rotation around the circle.
- The distance traveled by the particle is the total length of the path it covers.
- The length of the circumference of a circle is given by the formula:
Distance=2πr
- Since the particle completes one full rotation, the distance traveled is 2πr.
- Displacement is defined as the shortest distance from the initial position to the final position.
- In this case, the particle starts at a point (let's say point A) and after one complete rotation, it returns to the same point (point A).
- Therefore, the initial and final positions are the same, which means:
Displacement=0
- The distance traveled by the particle is 2πr.
- The displacement of the particle is 0.
- Distance = 2πr
- Displacement = 0
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]
Explore 35 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Write expression for circumference of a circle of radius 'r'
View SolutionA wheel 2 kg having practically all the mass concentrated along the circumference of a circle of radius 20 cm is rotating on its axis with angular velocity of 100 rad/s, then the rotational kinetic energy of wheel is
View Solution
Knowledge Check
If the circumference of a circle is 110 cm , find its radius .
A19.5 cm.B17.5 cm.C18.5 cm.D15.5 cm.
A particle travels along the arc of a circle of radius r. Its speed depends on the distance travelled l as v=a√l where 'a' is a constant. The angle α between the vectors of net acceleration and the velocity of the particle is
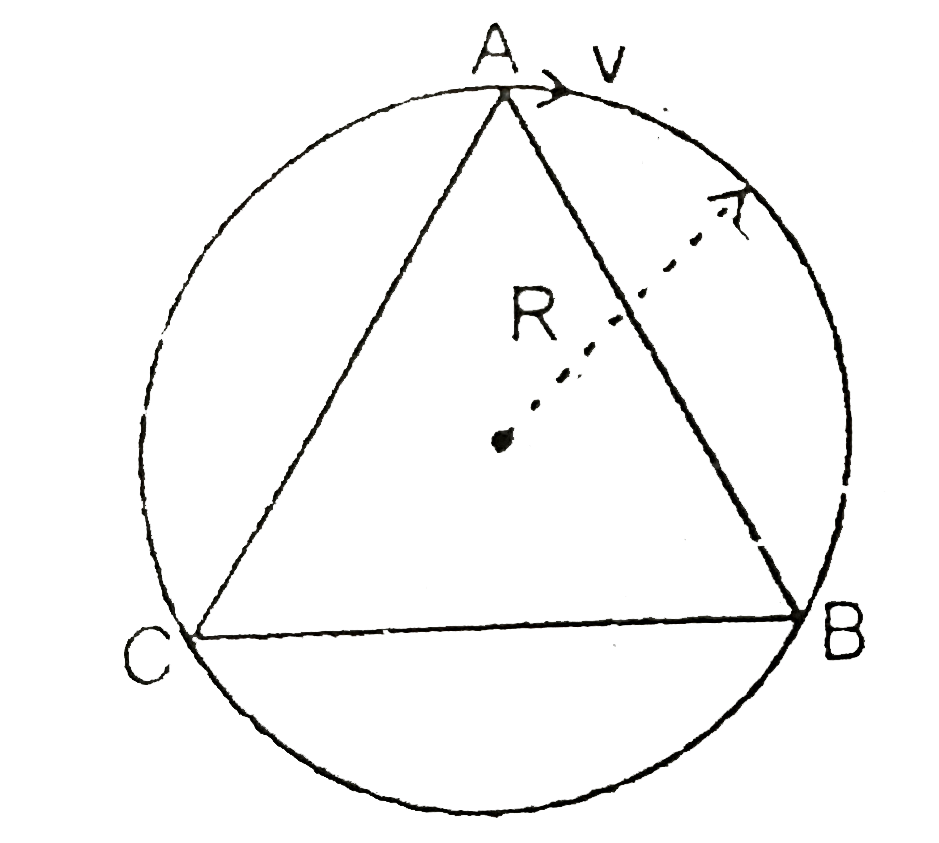
View SolutionA particle is moving with constant speed V m/s along the circumference of a circle of radius R meters as shown. A, B and C are three points on periphery of the circle and ΔABC is equilateral. The magnitude of average velocity of particle, as it moves from A to C in clockwise sence, will be :
View SolutionIF the circumference of a circle is 52.8cm, find its radius.
View SolutionA particle moves on a circular path of radius 'r'. It completes one revolution in 40s. Calculate distances displacement in 2 min 20 s.
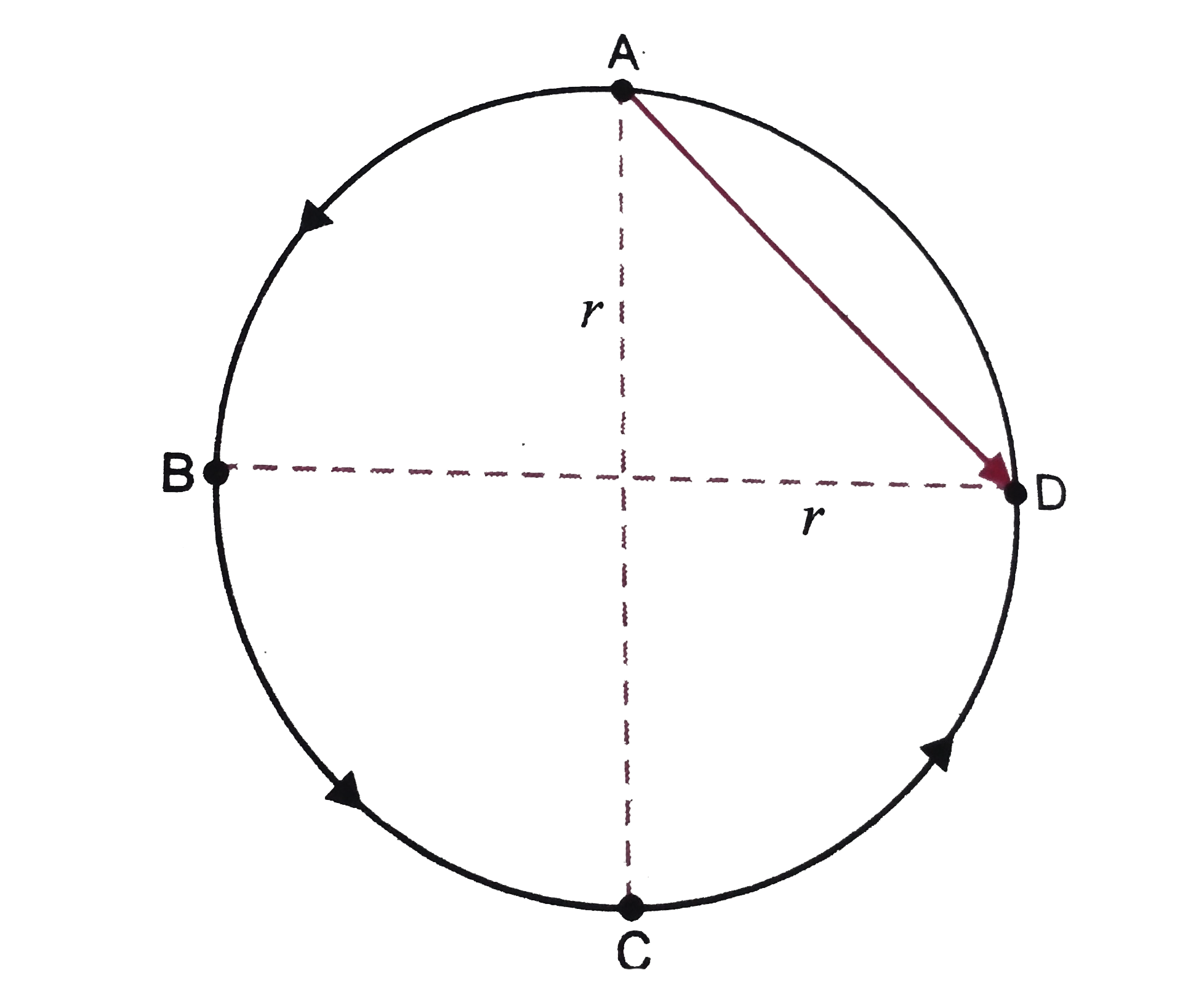
View SolutionA particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
View SolutionA cyclist rides along the circumference of a circular horizontal plane of radius R, with the friction coefficient μ=μ0(1−rR), where μ0 is constant and r is distance from centre of plane O. Find the radius of the circle along which the cyclist can ride with the maximum velocity, what is this valocity?

View SolutionA particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is
View Solution

