The position x of a particle varies with time t, as x=at2−bt3. The acceleration of the particle will be zero at time t equals to
2a3b
ab
a3b
zero
The correct Answer is:c
dx/dt=2at−3bt2,d2x/dt2=2a−6bt
t=2a/6b=a/3b
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]
Explore 35 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
The position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionThe position x of a particle varies with time t as x=at2−bt3. The acceleration at time t of the particle will be equal to zero, where (t) is equal to .
View SolutionThe position x of a particle varies with time t as x=at2−bt3. The acceleration at time t of the particle will be equal to zero, where (t) is equal to .
View SolutionIf the displacement of a particle varies with time as √x=t+3
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionThe velocity of a particle is zero at time t = 2s, then
View SolutionThe coordinates of a particle moving in XY-plane vary with time as x=4t2,y=2t. The locus of the particle is a : -
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
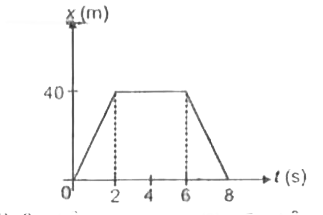
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionIf the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View Solution

