Two capicitors of capacitances 4and6μF respectively are connected in series across a pd of 250 V. These are disconnected and now connected in parallel. Find the new pd and charge on each capacitor.
To solve the problem, we will follow these steps:
Step 1: Calculate the total capacitance when capacitors are connected in series.
The formula for the total capacitance C of capacitors in series is given by:
1C=1C1+1C2
Where C1=4μF and C2=6μF.
Substituting the values:
1C=14+16
Finding a common denominator (which is 12):
1C=312+212=512
Thus,
C=125=2.4μF
Step 2: Calculate the charge on the capacitors when connected in series.
Using the formula for charge Q:
Q=C⋅V
Where V=250V.
Substituting the values:
Q=2.4×10−6F×250V=6×10−4C
Step 3: Calculate the potential difference across each capacitor when connected in series.
The voltage across each capacitor can be calculated using:
V1=QC1andV2=QC2
Calculating V1 for the 4μF capacitor:
V1=6×10−44×10−6=150V
Calculating V2 for the 6μF capacitor:
V2=6×10−46×10−6=100V
Step 4: Now, connect the capacitors in parallel.
In parallel, the total capacitance Ctotal is:
Ctotal=C1+C2=4μF+6μF=10μF
Step 5: Calculate the new potential difference across the capacitors in parallel.
The charge remains the same when the capacitors are switched from series to parallel. The new potential difference V across the capacitors can be calculated using:
V=QCtotal=6×10−410×10−6=60V
Step 6: Calculate the charge on each capacitor in parallel.
For the 4μF capacitor:
Q1=C1⋅V=4×10−6⋅60=240μC
For the 6μF capacitor:
Q2=C2⋅V=6×10−6⋅60=360μC
Summary of Results:
- New potential difference across both capacitors in parallel: 60 V
- Charge on 4μF capacitor: 240 μC
- Charge on 6μF capacitor: 360 μC
The formula for the total capacitance C of capacitors in series is given by:
Using the formula for charge Q:
The voltage across each capacitor can be calculated using:
In parallel, the total capacitance Ctotal is:
The charge remains the same when the capacitors are switched from series to parallel. The new potential difference V across the capacitors can be calculated using:
For the 4μF capacitor:
- New potential difference across both capacitors in parallel: 60 V
- Charge on 4μF capacitor: 240 μC
- Charge on 6μF capacitor: 360 μC
Similar Questions
Two capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionThree capcitors of capacitances 4μF,
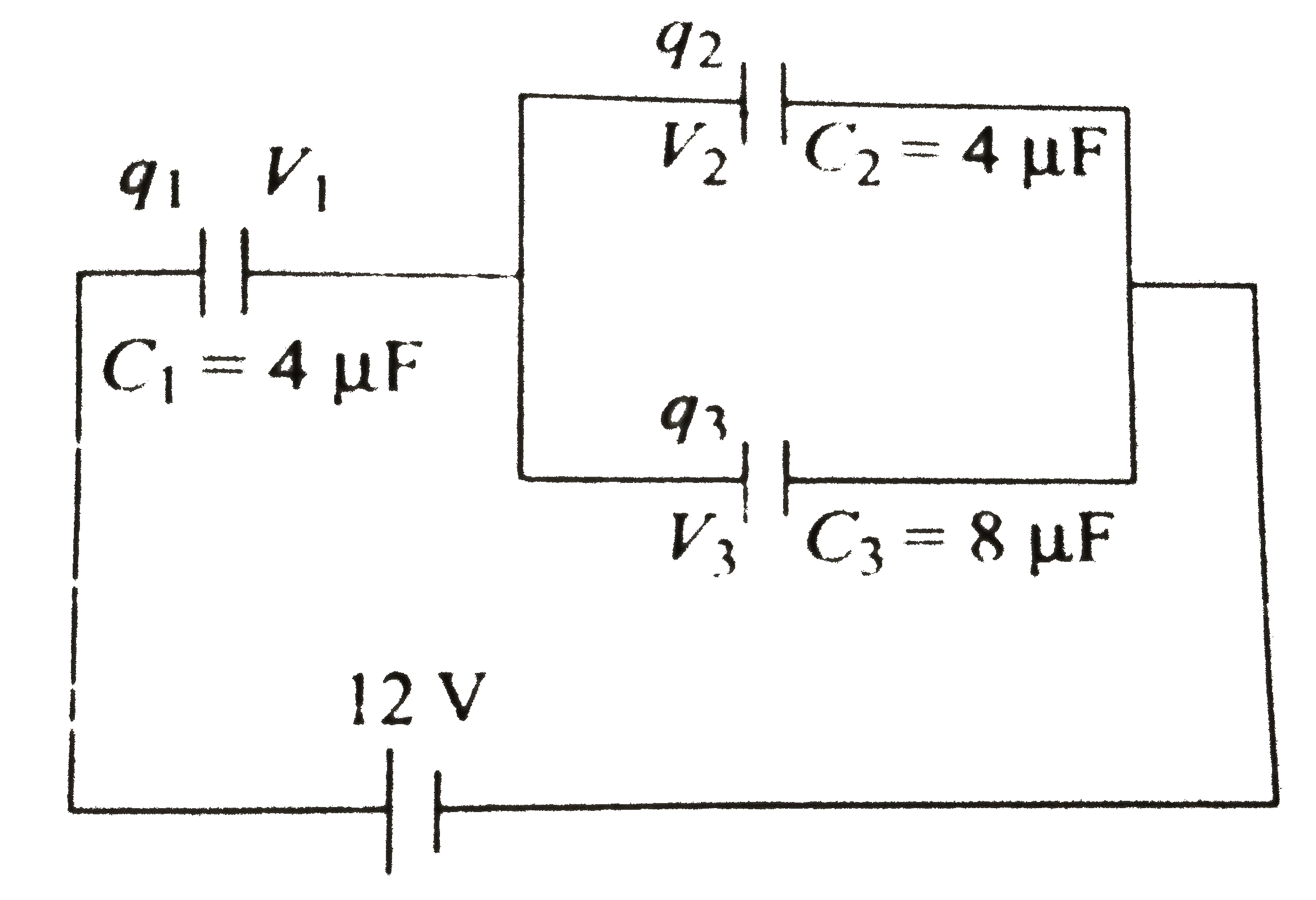 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
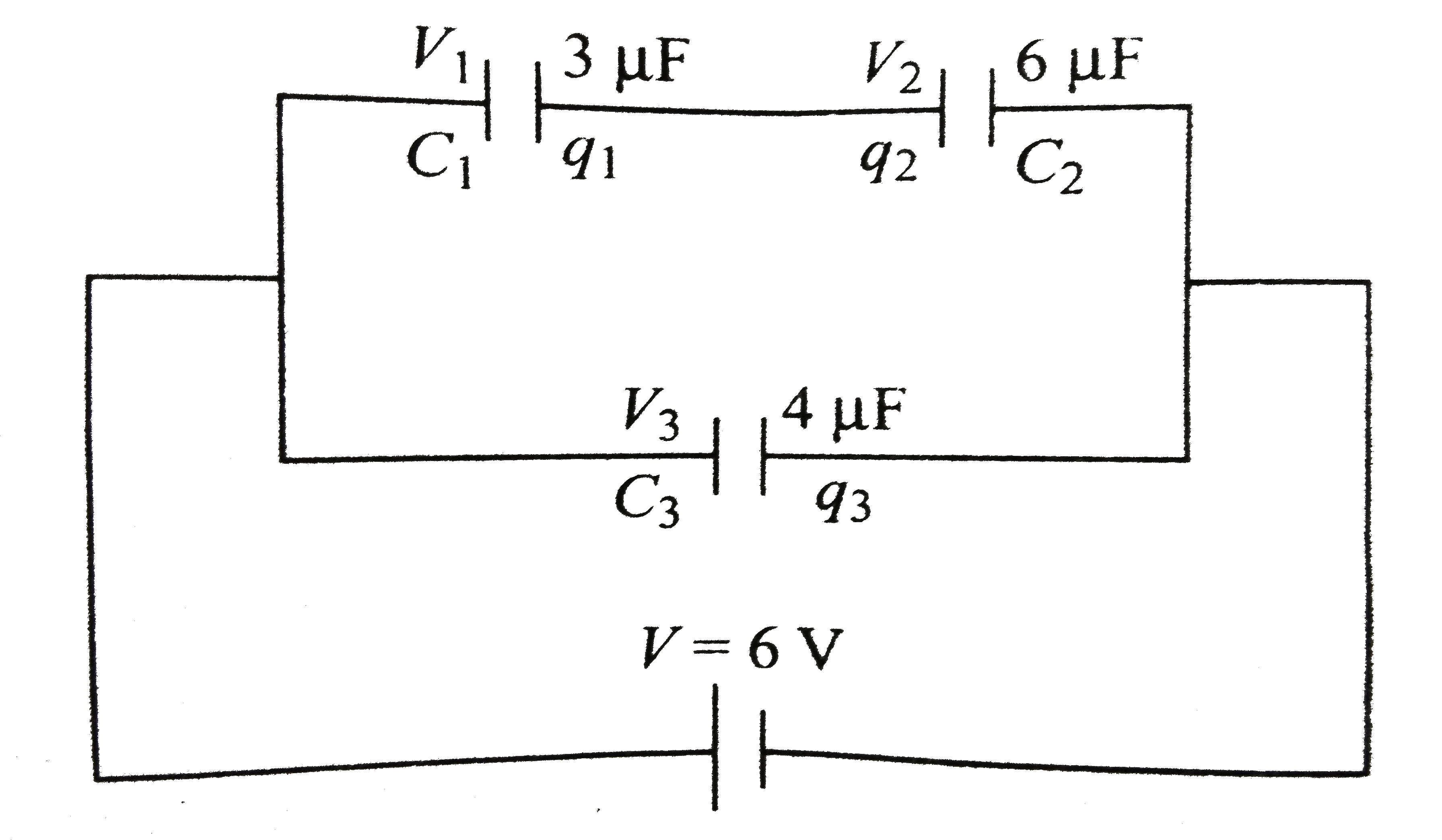
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View Solution

