Two capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.
To solve the problem step by step, we will address each part of the question sequentially.
Given:
- Capacitance of capacitor 1, C1=6μF
- Capacitance of capacitor 2, C2=3μF
- EMF of the cell, V=18V
(i) Calculate the equivalent capacitance Ceq:
For capacitors in series, the formula for equivalent capacitance is given by:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=16μF+13μF
Finding a common denominator (which is 6):
1Ceq=16+26=36=12
Now, taking the reciprocal to find Ceq:
Ceq=2μF
(ii) Calculate the potential difference across each capacitor:
The charge Q on the equivalent capacitor can be calculated using the formula:
Q=Ceq×V
Substituting the values:
Q=2μF×18V=36μC
Since the charge Q is the same on both capacitors in series, we can now find the potential difference across each capacitor.
1. Voltage across capacitor 1 (V1):
Using the formula V=QC:
V1=QC1=36μC6μF=6V
2. Voltage across capacitor 2 (V2):
V2=QC2=36μC3μF=12V
(iii) Calculate the charge on each capacitor:
As established earlier, the charge on each capacitor in series is the same:
- Charge on capacitor 1 (Q1): 36μC
- Charge on capacitor 2 (Q2): 36μC
Summary of Results:
1. Equivalent capacitance Ceq=2μF
2. Potential difference across capacitor 1 V1=6V and across capacitor 2 V2=12V
3. Charge on each capacitor Q1=Q2=36μC
- Capacitance of capacitor 1, C1=6μF
- Capacitance of capacitor 2, C2=3μF
- EMF of the cell, V=18V
- Charge on capacitor 2 (Q2): 36μC
1. Equivalent capacitance Ceq=2μF
2. Potential difference across capacitor 1 V1=6V and across capacitor 2 V2=12V
3. Charge on each capacitor Q1=Q2=36μC
Topper's Solved these Questions
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -1
60 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -2
36 Videos
- CALORIMETRY BOOK - MOTIONCHAPTER - CALORIMETRY EXERCISE - EXERCISE - 3 Section - B
4 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 4 Level-II
20 Videos
Similar Questions
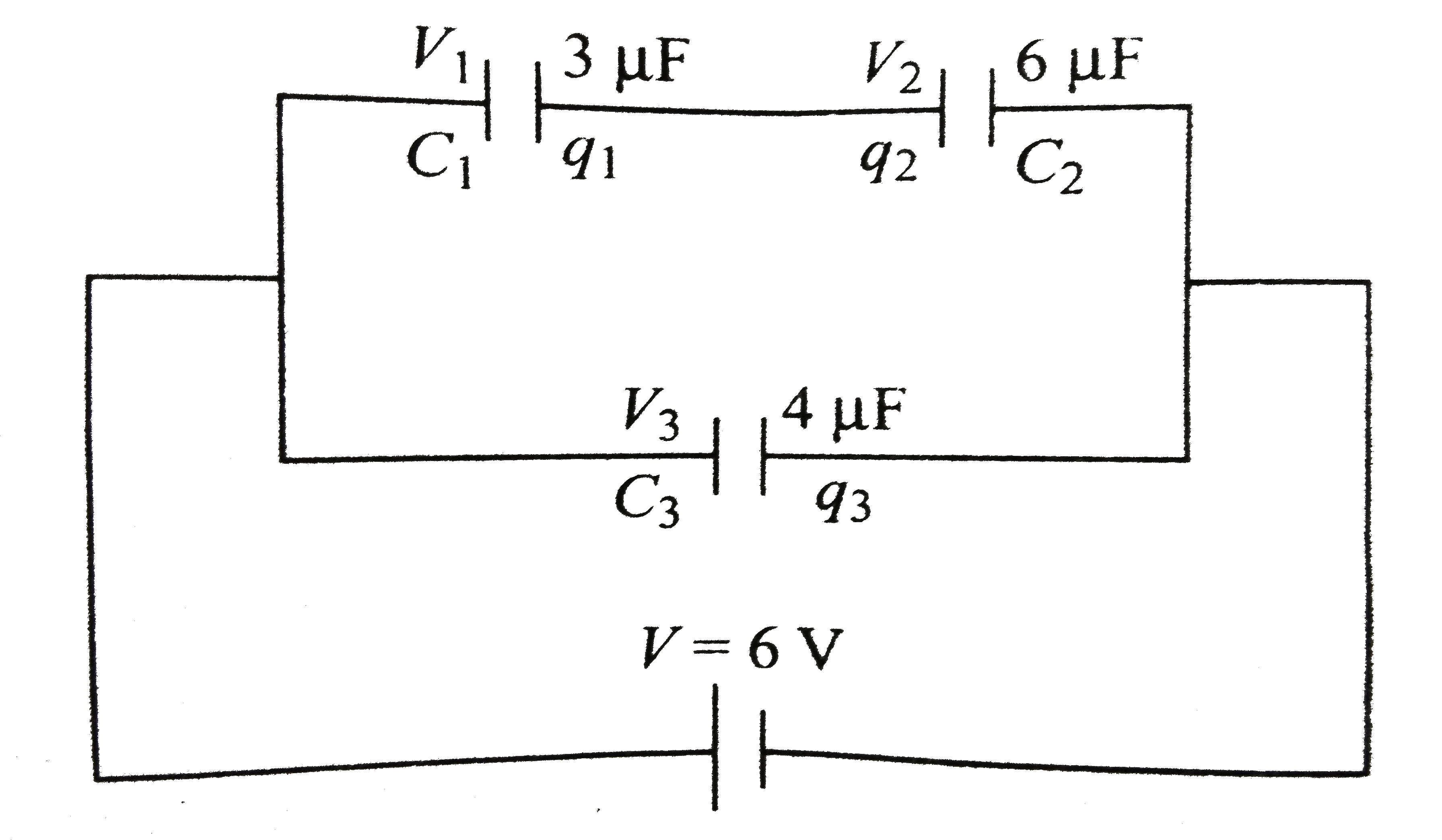
Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emg6V.
 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionThree capcitors of capacitances 4μF,
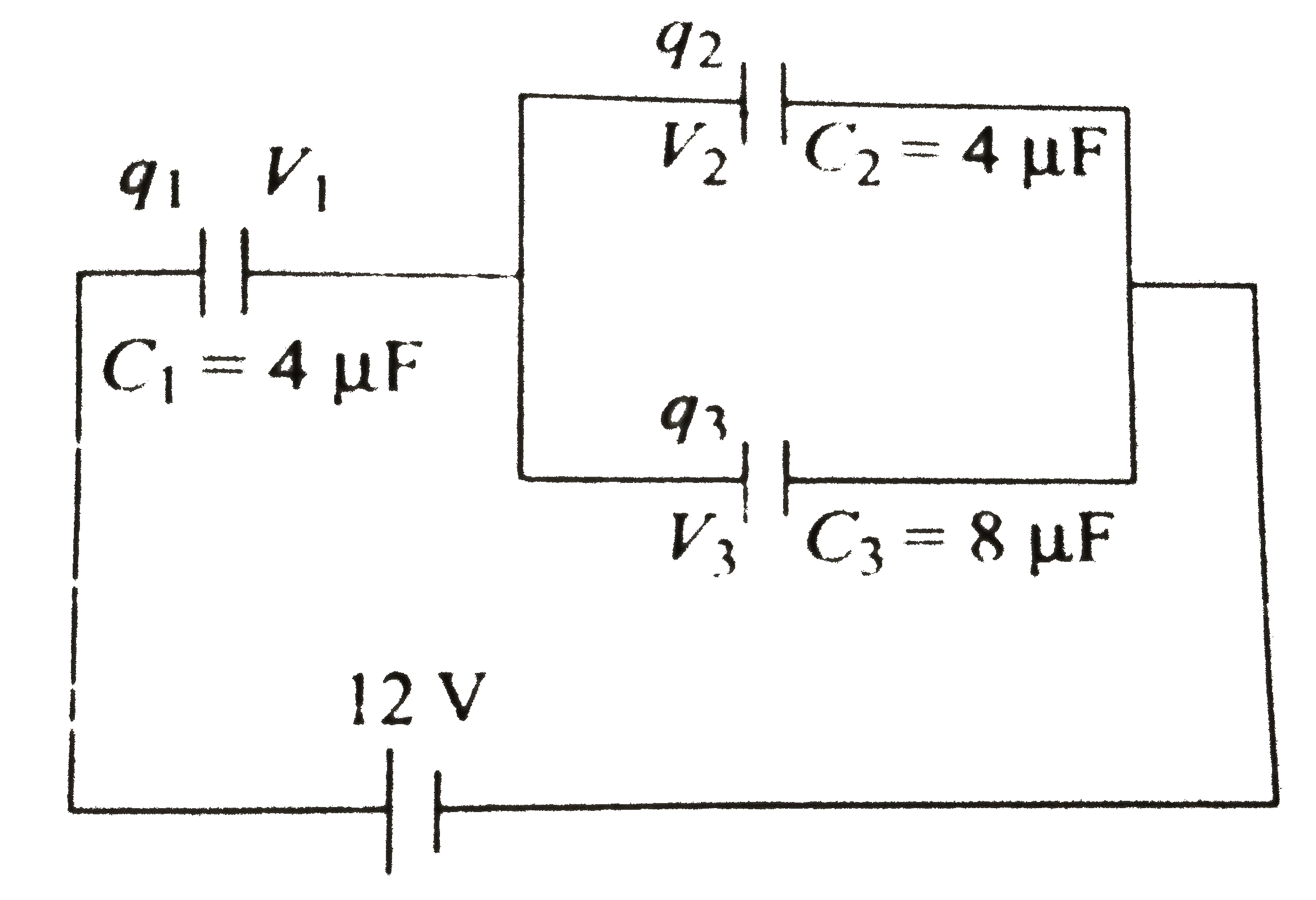 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
View Solution
Knowledge Check
Two capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
A66.67 V, 33.33 VB60 V, 40 VC50 V, 50 VD90 V, 10 VThree capacitors of capacitance 1μF,2μF and 3μF are connected in series and a potential difference of 11V is applied across the combination. Then, the potential difference across the plates of 1μF capacitor is
A2VB4VC1VD6VThree capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
A1:15B15:1C1:1D1:3
Four capacitors of capacitances 2 μF and 1μF are connected across a battery of 10V as shown in the figure (q). Calculate the net capacitance of the combination and net charge across each capacitor.
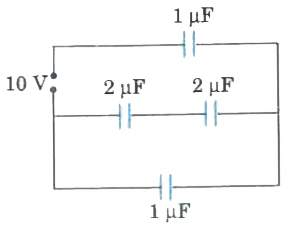
View SolutionTwo capacitors of capacitances 4μF and 6μF are connected in series with a battery of 20 V. find the energy supplied by the battery.
View SolutionTwo capacitors of capacitance C1=2μF and C2=8μF are connected in series and the resulting combination is connected across 300 volts. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors of capacitances 4μF and another two of 5μF are connected as shown in the given figure (f). Calculate the effective capacitance across points A and B.
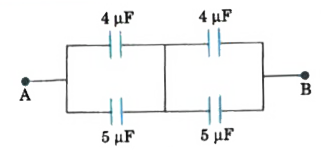
View Solution

