Two capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
Total charge on two capacitors
=C1V1+C2V2
(3×2+6×5)=36μC
In series combitions charge is conserved
Potential on 3μF capacitor =36μC3μF=12V
Potential on 6μF capacitor =36μC6μF=6V
Similar Questions
Two capacitors of capacitances 3μF&6μF are charged to potential of 2V and 5V respectively.These two charged capacitors are connected in series.Find the potential across C1
View SolutionTwo capacitors of capacitance 10 μF and 20 μF are charged to potential 20 V and 10 V respectively. If they are connected to share charges, then loss of energy is
View Solution
Knowledge Check
Two capacitor of capacitance 5μF and 10μF are charged to potential 40V and 10V respectively. Now the two capacitors ate connected with plates of same polarities together .
(A) the common potential will be 20V
(B) the final charges of capacitors will be 100μC and 200μC
(c) the ratio of total energy stored in capacitors before and after connection is 3:2
(D) the loss energy of system is 1500μJAA,B,CBB,C,DCA,B,DDA,B,C,DTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
A100B300C1000D3000Two capacitors of capacitances 1μFand3μF are charged to the same voltages 5V. They are connected in parallel with oppositely charged plates connected together. Then
AFinal common voltage will be 5VBFinal common voltage will be 2.5CHeat produced in the circuit will be zeroDHeat produced in the circuit will be 37.5μJ
Two capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionTwo capacitors A and B with capacitors 3μFand2μF are charged to a potential difference of 100 V and 180 V respectively. One plate of two capacitors are connected as shown. Now switch S is closed so as to connect a cell of 100 V to the free plates of two capacitors.
(a) Find charge on the two capacitors after the switch is closed.
(b) Calculate heat generated in the circuit
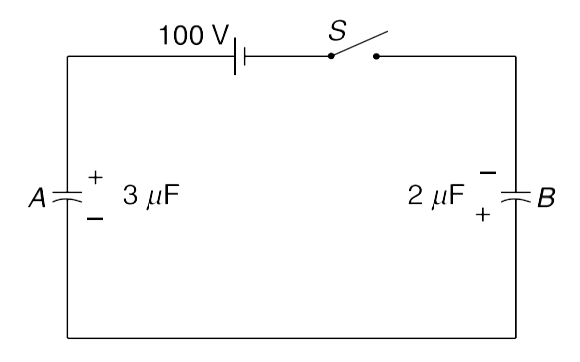
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionA capacitor of capacitance 6μF is charged to a potential of 150V. Its potential falls to 90V, when another uncharged capacitor is connected to it. Find the capacitance of the second capacitor and the amount of energy lost due to the connection.
View SolutionThree capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.
View Solution

